Как найти площадь фигуры

Изучение этой темы — важная часть математической программы начальной школы. Во 2–4 классах школьники начинают изучать площадь фигуры, учатся вычислять её и применять полученные знания на практике. Эта статья поможет ученикам понять, что такое площадь, как её обозначать, в каких единицах она измеряется и как находить площадь разных фигур с помощью простых формул.

Что такое площадь

Площадь — это величина, которая показывает, сколько места занимает фигура на плоскости. Представьте себе, что вы хотите покрасить стену или наклеить обои. Чтобы узнать, сколько краски или обоев вам нужно, сначала нужно узнать площадь стены. Таким образом, площадь помогает нам понять размер фигуры. Также площадь используется для расчёта территории участков земли, размеров паркета для комнаты и во многих других ситуациях.

Обозначение площади

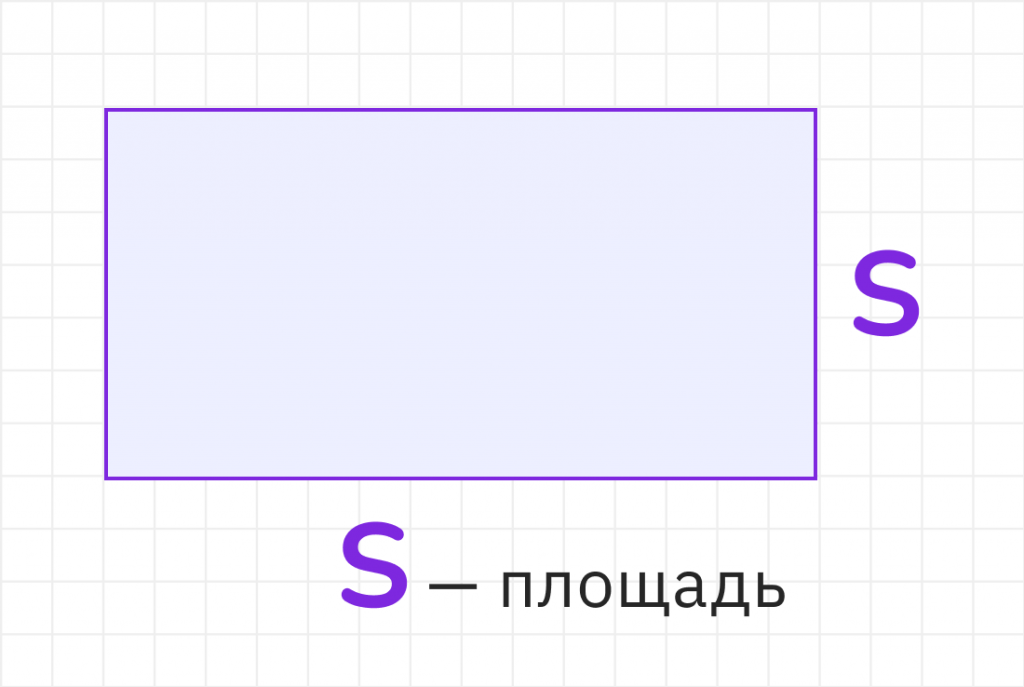
В математике площадь обозначается буквой S. Например, площадь квадрата можно обозначить как S_квадрат​, площадь прямоугольника — S_прямоугольник​. Это упрощает записи и делает их более понятными. 

Единицы измерения площади

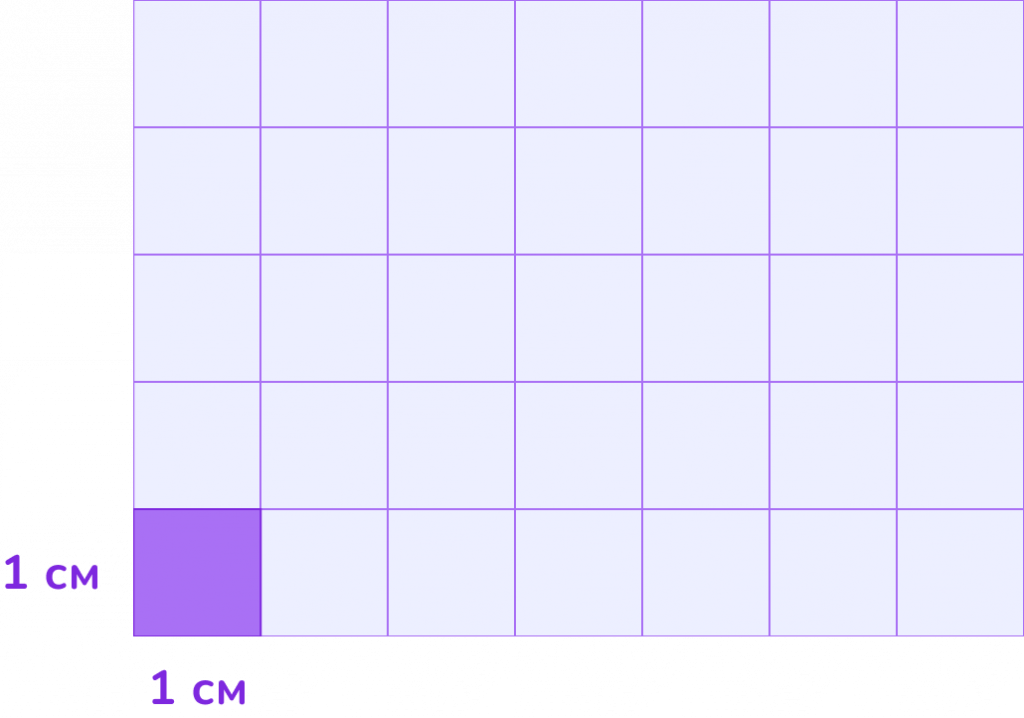
Площадь измеряется в квадратных единицах. Основные единицы измерения площади — квадратные сантиметры (см²), квадратные метры (м²), квадратные миллиметры (мм²) и квадратные километры (км²). Если сторона квадрата равна 1 см, его площадь будет: 

1 см ∙ 1 см = 1 см². Таким образом, площадь показывает, сколько таких квадратов нужно, чтобы заполнить фигуру.

Иногда площадь измеряется в других единицах, например, гектары (га), которые используются для измерения земельных участков. Один гектар равен 10 000 м².

Формулы нахождения площади

Для разных фигур используются разные формулы для вычисления площади. Рассмотрим их подробнее.

1. Прямоугольник

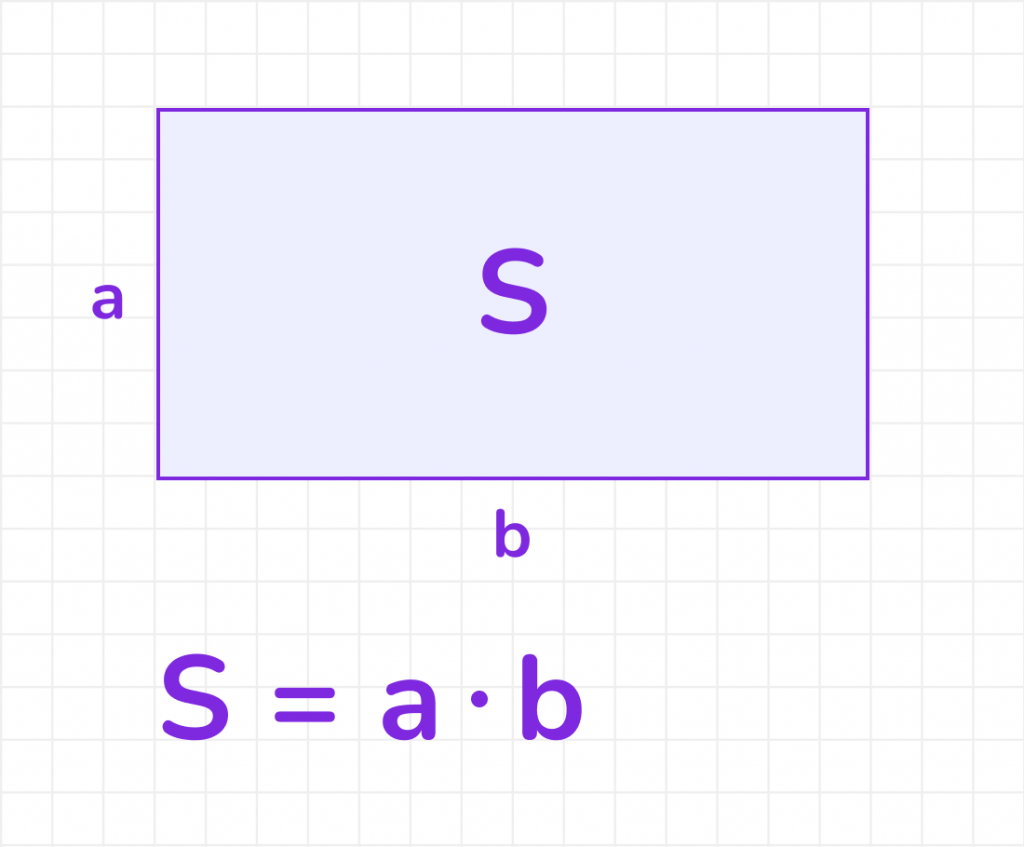
Прямоугольник имеет две пары противоположных сторон, которые равны. Чтобы найти площадь прямоугольника, нужно умножить его длину на ширину: 

S_прямоугольник = a ∙ b,  где a и b — длины сторон прямоугольника.

Задачи для тренировки:

1. Найдите площадь прямоугольника с длиной 7 см и шириной 5 см.

(S = 35 см²)

2. Прямоугольник имеет длину 8 см и ширину 5 см. Какова его площадь?

(S = 40 см²)

3. Найдите площадь прямоугольника, если его длина равна 12 см, а ширина — 6 см.

(S = 72 см²)

4. Дан прямоугольник с длиной 9 см и шириной 3 см. Вычислите его площадь.

(S = 27 см²)

5. Прямоугольник имеет длину 15 см и ширину 10 см. Найдите его площадь.

(S = 150 см²)

2. Квадрат

Квадрат — это особый вид прямоугольника, у которого все стороны равны. Площадь квадрата вычисляется умножением длины его стороны на саму себя: 

S_квадрат = a ∙ a = a², где a — длина стороны квадрата.

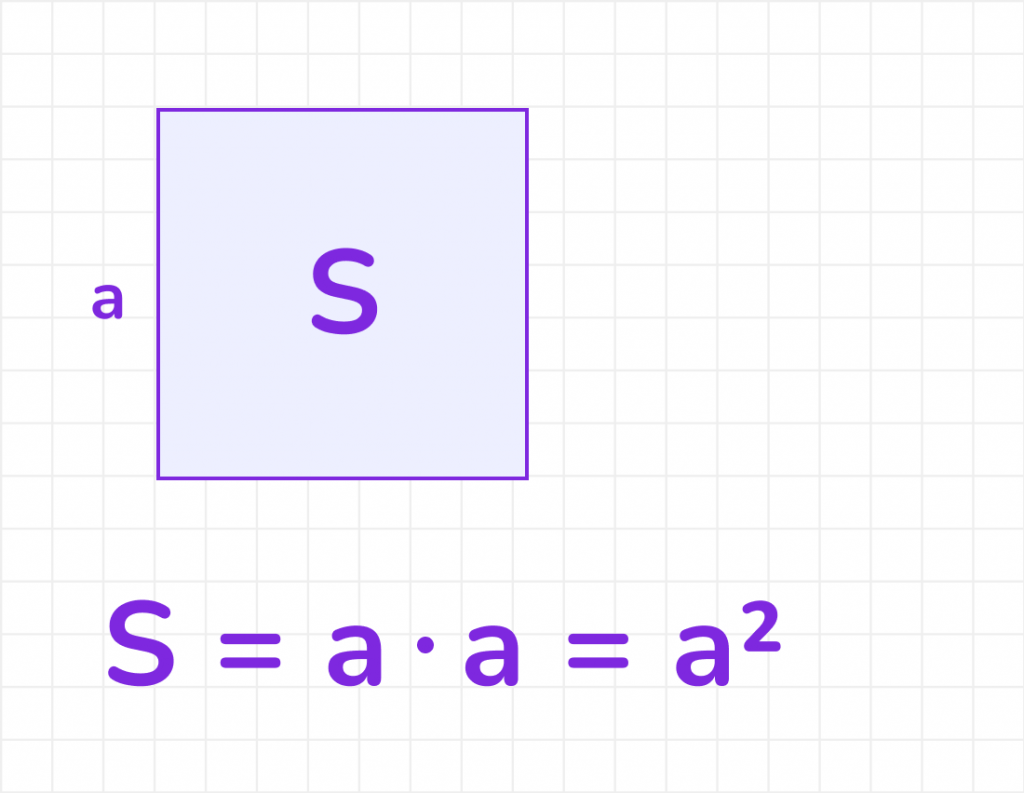
Задачи для тренировки:

1. Найдите площадь квадрата со стороной 5 см. 

(S = 25 см²)

2. Квадрат имеет сторону 7 см. Какова его площадь? 

(S = 49 см²)

3. Вычислите площадь квадрата со стороной 10 см. 

(S = 100 см²)

4. Найдите площадь квадрата, если его сторона равна 12 см. 

(S = 144 см²)

5. Квадрат со стороной 3 см. Какова его площадь?

(S = 9 см²)

3. Прямоугольный треугольник

Прямоугольный треугольник имеет один прямой угол. Площадь прямоугольного треугольника можно найти, умножив длины двух сторон, образующих прямой угол, и разделив результат на два: S_прямоугольный треугольник = (a ∙ b) : 2, где a и b — длины катетов треугольника.

Задачи для тренировки:

1. Найдите площадь прямоугольного треугольника с катетами 5 см и 12 см.

(S = 30 см²)

2. Прямоугольный треугольник имеет катеты 8 см и 15 см. Какова его площадь?

(S = 60 см²)

3. Вычислите площадь прямоугольного треугольника с катетами 7 см и 24 см.

(S = 84 см²)

4. Найдите площадь прямоугольного треугольника, если его катеты равны 9 см и 12 см.

(S = 54 см²)

5. Дан прямоугольный треугольник с катетами 6 см и 10 см. Какова его площадь?

(S = 30 см²)

Решение задач на нахождение площади

Рассмотрим несколько примеров задач на нахождение площади.

Пример 1: Найдите площадь прямоугольника с длиной 5 см и шириной 3 см. 

Решение: S = 5 см ∙ 3 см = 15 см².

Пример 2: Найдите площадь квадрата со стороной 4 см. 

Решение: S = 4 см ∙ 4 см = 16 см².

Пример 3: Найдите площадь прямоугольного треугольника с катетами 6 см и 8 см. 

Решение: S = (6 см ∙ 8 см) : 2 = 24 см².

Задачи для тренировки:

1. Найдите площадь прямоугольника с длиной 8 см и шириной 2 см.

(S = 16 см²)

2. Квадрат имеет сторону 9 см. Какова его площадь?

(S = 81 см²)

3. Вычислите площадь прямоугольного треугольника с катетами 5 см и 6 см.

(S = 15 см²)

4. Найдите площадь прямоугольника с длиной 10 см и шириной 4 см.

(S = 40 см²)

5. Прямоугольный треугольник имеет катеты 7 см и 8 см. Какова его площадь?

(S = 28 см²)

Площадь сложных фигур

Иногда фигуры бывают сложными и состоят из нескольких простых фигур. В таких случаях можно разделить сложную фигуру на простые части, найти площадь каждой части, а затем сложить их площади. Это позволяет вычислить площадь сложных фигур,  ограниченных линиями.

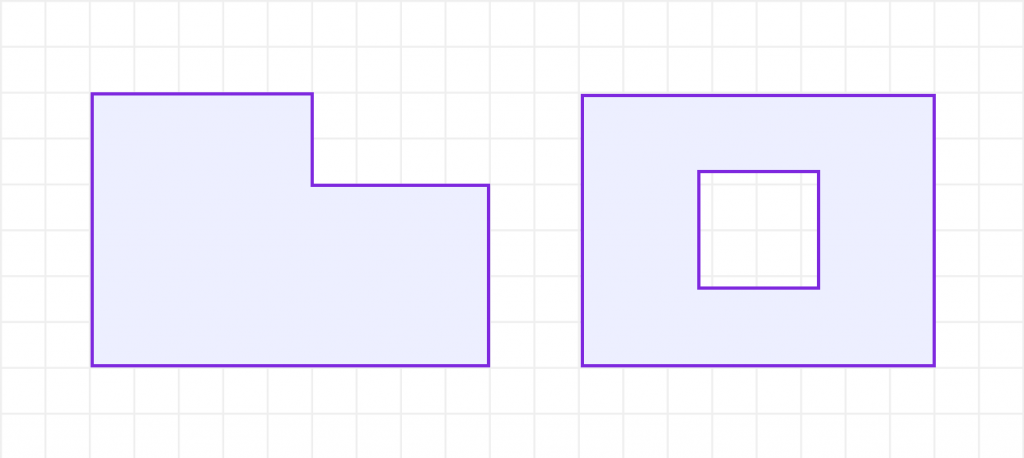
Решение задач на нахождение площади сложных фигур

Пример 1: Найдите площадь фигуры, состоящей из прямоугольника размером 5 см на 3 см и квадрата со стороной 2 см, присоединённого к одной из сторон прямоугольника.

Сначала найдём площадь прямоугольника: 

S_прямоугольник = 5 см ∙ 3 см = 15 см².

Теперь найдём площадь квадрата: 

S_квадрат = 2 см ∙ 2 см = 4 см².

Сложим площади: 

S_общая = 15 см² + 4 см² = 19 см².

Пример 2: Найдите площадь изображённой фигуры.

Сначала разделим фигуру на две простые: 

Найдём площадь первой фигуры: 

S_1 = 4 см ∙ 5 см = 20 см².

Найдём стороны второй фигуры: 

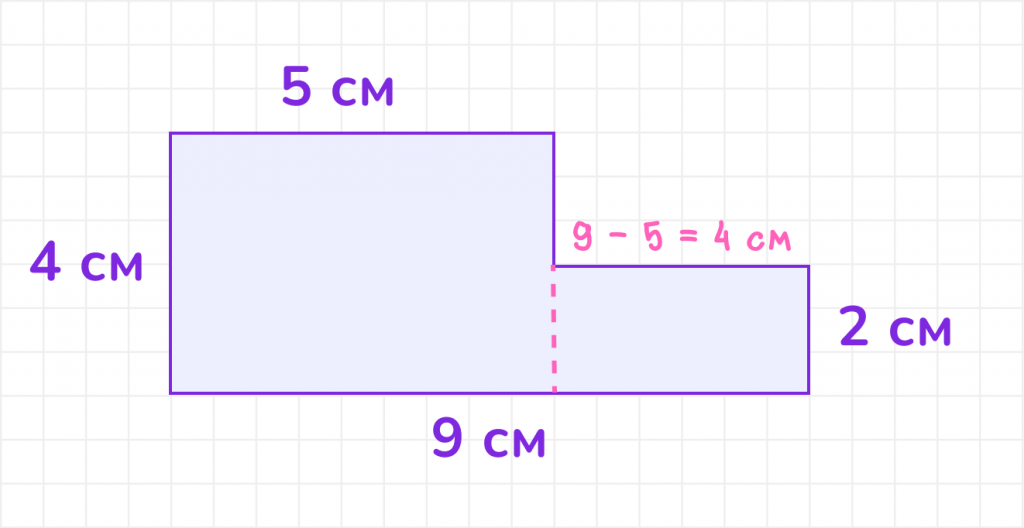
Теперь найдём площадь второй фигуры: 

S_2 = 4 см ∙ 2 см = 8 см².

Сложим площади: 

S_общая = 20 см² + 8 см² = 28 см².

Задачи для тренировки:

1. Фигура состоит из квадрата со стороной 4 см и прямоугольного треугольника с катетами 3 см и 4 см. Найдите её площадь. 

(S = 22 см²)

2. Найдите площадь фигуры, состоящей из двух квадратов со сторонами 2 см и 3 см, присоединённых друг к другу.

(S = 13 см²)

3. Фигура состоит из прямоугольника с длиной 10 см и шириной 5 см и квадрата со стороной 2 см. Найдите её площадь.

(S = 54 см²)

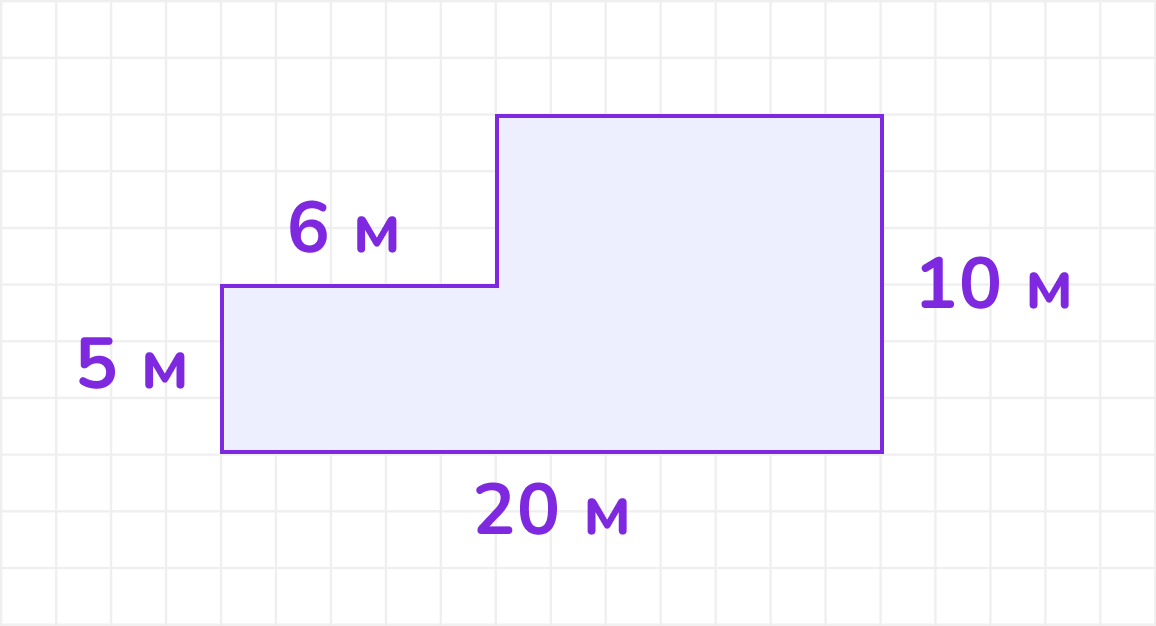
4. Вычислите площадь изображённой фигуры.

(S = 170 м²)

Итак, нам удалось узнать:

1. Что такое площадь и как она обозначается.
2. Какие единицы измерения площади существуют.
3. Как вычислить площадь различных фигур: прямоугольника, квадрата, прямоугольного треугольника.
4. Как находить площадь сложных фигур, разделяя их на простые части.

Если ребёнок испытывает трудности в нахождении площади фигур, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия.

Популярные статьи по математике:

1. Как найти периметр и площадь прямоугольника и квадрата
2. Как найти площадь треугольника
3. Длина окружности и площадь круга