Как найти периметр треугольника

В начальных классах школьники начинают изучать основные геометрические фигуры и их свойства. Одним из важных понятий в геометрии является периметр. На уроках математики, начиная с 1 класса, ученики знакомятся с этим понятием, узнают, что такое периметр и как его вычислить. В этой статье мы подробно разберём, что такое периметр треугольника, как его найти и какие формулы для этого использовать. 

Что такое периметр

Периметр — это сумма длин всех сторон геометрической фигуры. Для треугольника это означает, что нужно сложить длины всех его сторон. Периметр измеряется в тех же единицах, в которых измеряются стороны фигуры, например, в сантиметрах или метрах. Представьте себе забор вокруг сада. Чтобы узнать, сколько метров забора вам понадобится, нужно измерить длину каждой стороны сада и сложить эти длины. Это и будет периметр.

Определение периметра фигуры

Периметр фигуры — это общая длина её границы. Если мы возьмём любую геометрическую фигуру, например, квадрат, прямоугольник или треугольник, то для нахождения её периметра нужно сложить длины всех сторон. Периметр важен для понимания размера и формы фигуры. Например, если мы хотим окаймить клумбу бордюром, то для определения количества материала нам нужно знать периметр клумбы.

Единицы измерения периметра

Периметр измеряется в единицах длины. Самыми распространёнными единицами измерения являются миллиметры (мм), сантиметры (см), метры (м) и километры (км). В задачах чаще всего используют сантиметры и метры. Например, длина карандаша может быть измерена в сантиметрах, а длина футбольного поля — в метрах. Важно выбирать правильные единицы измерения, чтобы результаты были точными и понятными.

Формула нахождения периметра треугольника

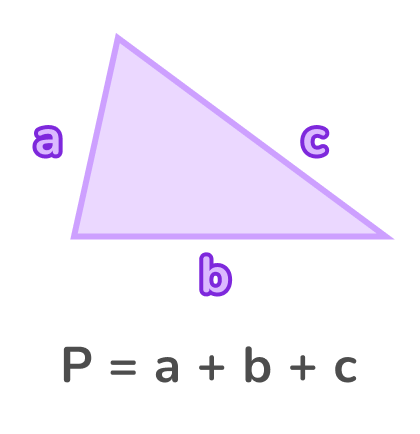
Для нахождения периметра треугольника нужно сложить длины всех его сторон. Обозначим стороны треугольника буквами a, b и c. Тогда формула для нахождения периметра треугольника будет выглядеть так:

P = a + b + c

где P — периметр треугольника, a, b, c — длины его сторон. Эта формула проста и легко запоминается. Рассмотрим эту формулу на примерах.

1️⃣ Периметр разностороннего треугольника

Разносторонний треугольник — это треугольник, у которого все стороны имеют разные длины. Для нахождения периметра разностороннего треугольника нужно сложить длины всех его сторон. Например, если стороны равны 3 см, 4 см и 5 см, то периметр будет равен:

P = 3 см + 4 см + 5 см = 12 см.

В данном случае мы просто сложили все стороны и получили периметр.

2️⃣ Периметр равнобедренного треугольника

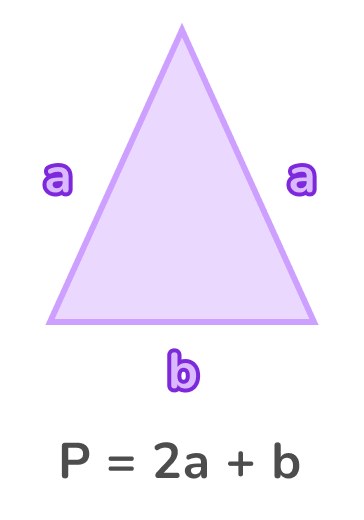
Равнобедренный треугольник — это треугольник, у которого две стороны равны. Обозначим длину равных сторон буквой a, а длину третьей стороны — буквой b. Тогда формула для нахождения периметра равнобедренного треугольника будет выглядеть так:

P = 2a + b.

Например, если длины равных сторон равны 5 см, а длина основания равна 6 см, то периметр равнобедренного треугольника будет равен:

P = 2 ∙ 5 см + 6 см = 10 см + 6 см = 16 см.

В этом примере мы умножили длину одной из равных сторон на два, чтобы учесть обе стороны, а затем добавили длину основания.

3️⃣ Периметр равностороннего треугольника

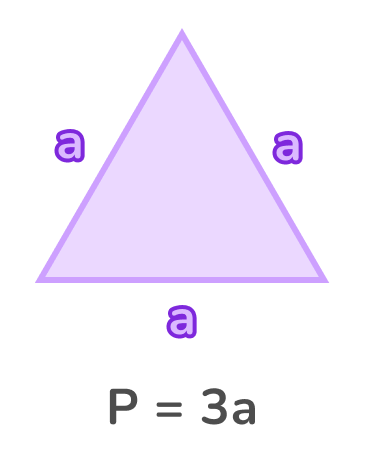
Равносторонний треугольник — это треугольник, у которого все стороны равны. Обозначим длину стороны равностороннего треугольника буквой a. Тогда формула для нахождения периметра равностороннего треугольника будет выглядеть так: P = 3a.

Например, если длина стороны равностороннего треугольника равна 4 см, то периметр равностороннего треугольника будет равен:

P = 3 ∙ 4 см = 12 см.

Здесь мы просто умножаем длину одной стороны на три, так как все стороны равны.

Решение задач на нахождение периметра треугольников

Для лучшего понимания рассмотрим несколько примеров задач на нахождение периметра треугольников.

➤ Пример 1: Разносторонний треугольник

Найдите периметр треугольника, если длины его сторон равны 5 см, 7 см и 9 см.

Решение: Используем формулу для разностороннего треугольника P = a + b + c.

P = 5 см + 7 см + 9 см = 21 см.

Ответ: Периметр треугольника равен 21 см.

➤ Пример 2: Равнобедренный треугольник

Найдите периметр равнобедренного треугольника, если длины его равных сторон равны 8 см, а длина основания равна 6 см.

Решение: Используем формулу для равнобедренного треугольника P = 2a + b.

P = 2 ∙ 8 см + 6 см = 16 см + 6 см = 22 см.

Ответ: Периметр равнобедренного треугольника равен 22 см.

➤ Пример 3: Равносторонний треугольник

Найдите периметр равностороннего треугольника, если длина его стороны равна 5 см.

Решение: Используем формулу для равностороннего треугольника P = 3a.

P = 3 ∙ 5 см = 15 см.

Ответ: Периметр равностороннего треугольника равен 15 см.

Задачи для тренировки

➜ Задача 1. Найдите периметр треугольника, если его стороны равны 6 см, 8 см и 10 см.

Решение: Для нахождения периметра треугольника используем общую формулу P = a + b + c.

P= 6 см + 8 см + 10 см = 24 см.

Ответ: периметр треугольника равен 24 см.

➜ Задача 2. Периметр равнобедренного треугольника равен 20 см. Найдите длины его равных сторон, если длина основания равна 8 см.

Решение: Пусть длины равных сторон равны a. Тогда используем формулу для периметра равнобедренного треугольника P = 2a + b.

20 = 2a + 8.

Решаем уравнение:

2a = 20 − 8;

2a = 12;

a = 6.

Ответ: длины равных сторон равны 6 см.

➜ Задача 3. Найдите периметр равностороннего треугольника, если длина его стороны равна 7 см.

Решение: Используем формулу для равностороннего треугольника P = 3a.

P = 3 ∙ 7 см = 21 см.

Ответ: периметр равностороннего треугольника равен 21 см.

➜ Задача 4. Найдите периметр треугольникa, если его стороны равны 7 см, 24 см и 25 см.

Решение: Для нахождения периметра используем формулу

P = a + b + c.

P = 7 см + 24 см + 25 см = 56 см.

Ответ: периметр треугольника равен 56 см.

➜ Задача 5. Периметр равностороннего треугольника равен 33 см. Найдите длину его стороны.

Решение: Используем формулу для периметра равностороннего треугольника P=3a.

33 = 3a.

Решаем уравнение:

a = 33 : 3;

a = 11 см.

Ответ: длина стороны равностороннего треугольника равна 11 см.

Изучение периметра треугольников важно для понимания основных геометрических понятий и навыков. Решение задач на нахождение периметра помогает ученикам закрепить полученные знания и применять их на практике. 

Итак, нам удалось узнать:

1. Что такое периметр и как его определить.
2. Какие единицы измерения используются для периметра.
3. Kак найти периметр разностороннего треугольника.
4. Как найти периметр равнобедренного треугольника.
5. Kак найти периметр равностороннего треугольника.
6. Как решать задачи на нахождение периметра треугольников.

Если ребёнок испытывает трудности в нахождении периметра треугольников, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия 💜

Популярные статьи:

1. Как найти периметр и площадь прямоугольника и квадрата
2. Как найти время, скорость, расстояние
3. Таблица умножения: как выучить легко и быстро