Квадратные уравнения: алгоритмы решения
Квадратные уравнения — это уравнения вида aх2+bx+c=0, где коэффициенты a, b,c — это некоторые числа, причём a ≠ 0.
Решить квадратное уравнение — это значит найти все его корни или, напротив, установить, что корней нет.
Есть два самых распространённых способа решения таких уравнений: первый — с помощью формулы корней, второй — с помощью теоремы Виета. В статье мы рассмотрим оба варианта, чтобы вы могли выбрать более удобный для вас.
Основные понятия квадратных уравнений
Чтобы при изучении темы не возникало сложностей с пониманием определений, давайте рассмотрим основные понятия квадратных уравнений.
- Приведённое квадратное уравнение — это уравнение, в котором коэффициент а=1.
- Неприведённое квадратное уравнение — это уравнение, в котором коэффициент а≠1.
- Полное квадратное уравнение — это уравнение, в котором все коэффициенты отличны от нуля.
- Неполное квадратное уравнение — это уравнение, в котором хотя бы один коэффициент равен нулю.
Решение квадратных уравнений с помощью формулы корней
Также для удобства решения существуют свойства коэффициентов квадратного уравнения, а именно:
1. если сумма коэффициентов квадратного уравнения равна 0 (a + b + c = 0), то:
2. если сумма коэффициентов а и с равна коэффициенту b (а + с = b), то:
Способы решения неполных квадратных уравнений
Решение квадратных уравнений с помощью теоремы Виета
На практике теорема Виета чаще всего применяется для решения приведённых квадратных уравнений.
Важное условие для применения теоремы Виета — это уравнение должно иметь корни, то есть — D≥0.
Для приведённого квадратного уравнения х2+px+q=0, согласно теореме Виета, верно следующее:
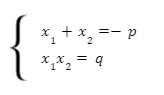
Рассмотрим алгоритм решения приведенных квадратных уравнений с помощью теоремы Виета:
Итак, теперь вы знаете, как решать квадратные уравнения двумя способами: с помощью формулы корней и теоремы Виета. Потренируйтесь самостоятельно, чтобы закрепить информацию. Или приходите на занятия в нашу онлайн-школу! Разберём любые темы, которые вызывают у вас сложности 💜
105
79
60
Контроль качества занятий 
Интерактивная платформа 
Норм
Есть вода, есть бесполезные частности, по сути запоминать столько всего ребёнку будет тяжело
Не знала свойства коэффициентов квадратного уравнения, теперь знаю
Лучшее объяснение, что я когда-либо видел
Замечательно. Вспомнила всё решение квадратного уравнения, могу теперь объяснить сыну.