
Основные геометрические фигуры
Геометрия — предмет, который появляется в расписании школьников только в 7-м классе. Но первое знакомство с миром форм начинается уже в начальной школе. Какие геометрические фигуры нас окружают? Каковы их отличительные особенности? А также чем геометрические фигуры отличаются от геометрических тел? На эти и другие вопросы ищите ответы в статье.

Базовые геометрические фигуры
Самая простая, можно сказать изначальная, геометрическая фигура — точка. Точки обозначают заглавными латинскими буквами. Они служат строительным материалом для других геометрических фигур.

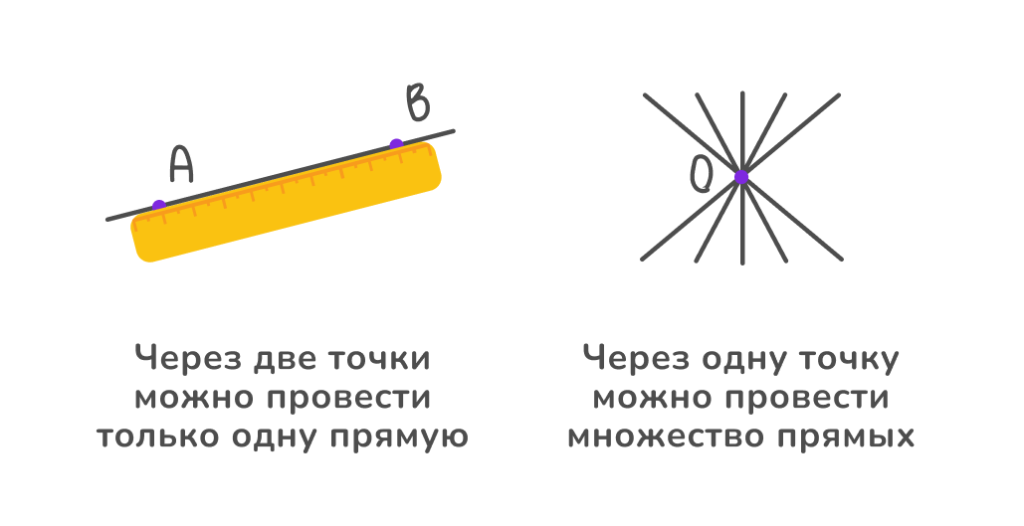
Линия, не имеющая ни начала, ни конца, простирающаяся бесконечно в двух противоположных направлениях называется прямая. Прямые обозначают строчными латинскими буквами.
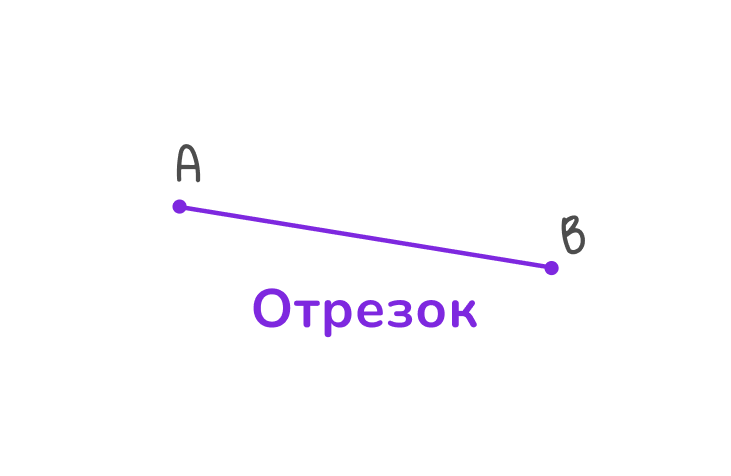
Отрезок — это часть прямой, ограниченная двумя точками, которые являются его началом и концом. Отрезок имеет длину, которую можно измерить.
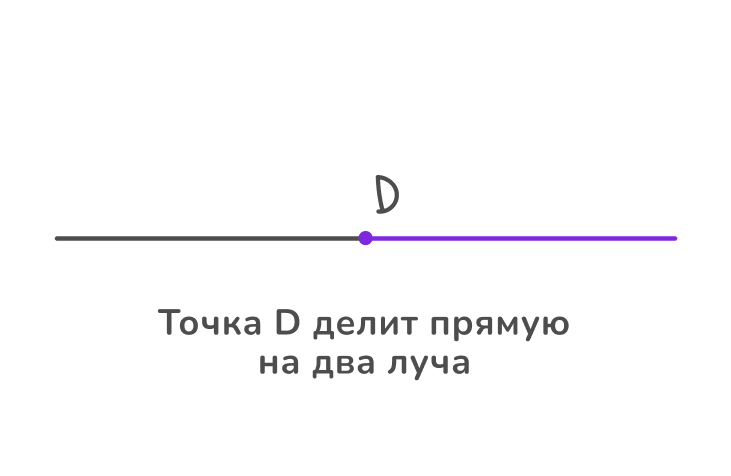
Если на прямой поставить только одну точку, то она разделит линию на два луча. Луч имеет начало, но не имеет конца, поэтому может быть бесконечно продолжен только в одну сторону.
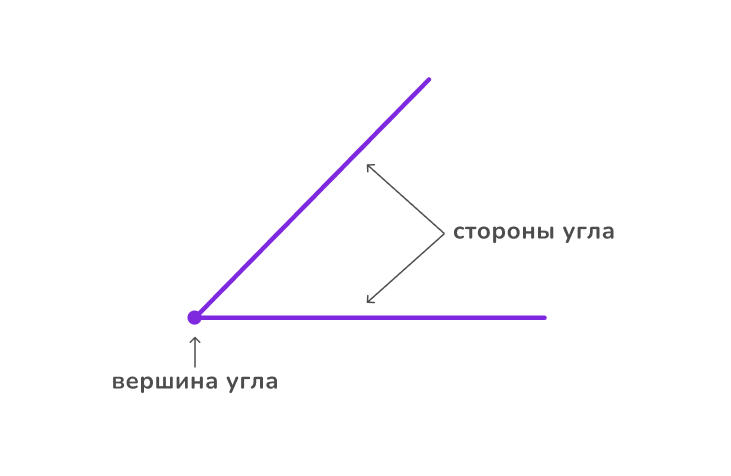
Когда из одной точки исходят два луча, то они образуют угол. При этом точку называют вершиной угла, а лучи — его сторонами.
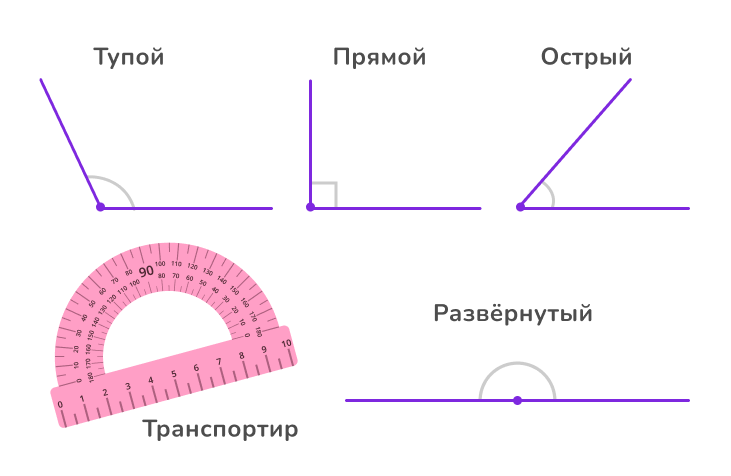
Углы измеряются в градусах с помощью специального инструмента — транспортира. В зависимости от численной меры угла они подразделяются на прямые (90°), тупые (более 90°) и острые (менее 90°). Отдельным видом углов считаются развёрнутые (угол 180°).
Прямоугольник и квадрат
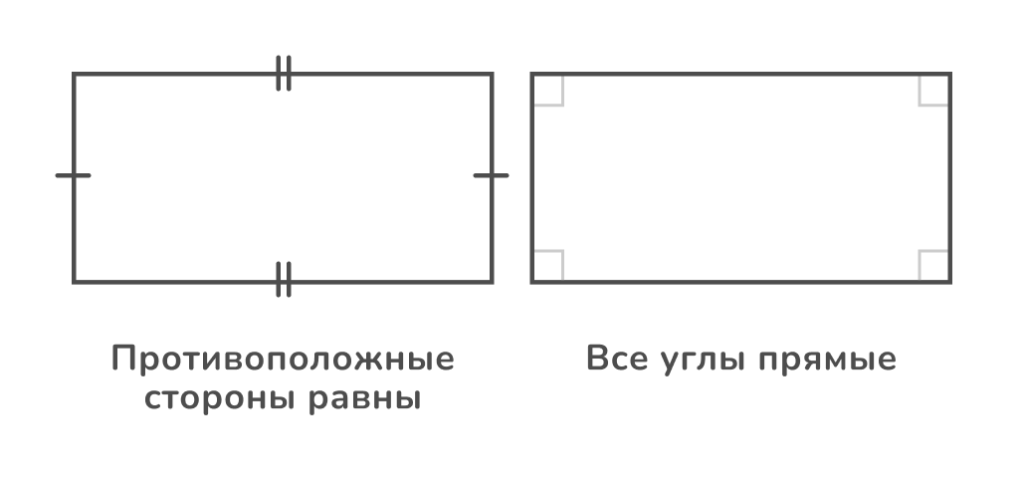
Четырёхугольник, у которого все четыре угла прямые, — прямоугольник. У прямоугольника противоположные стороны равны и параллельны.
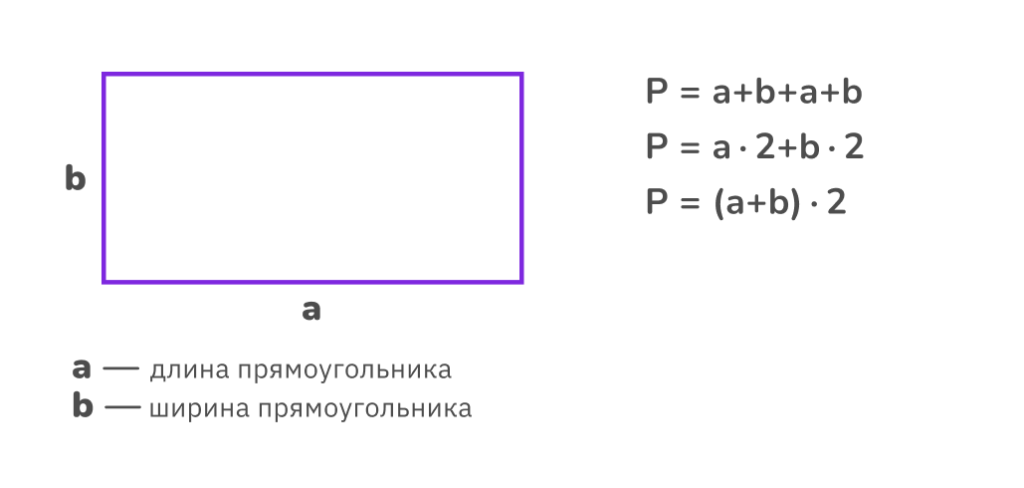
Чтобы вычислить периметр прямоугольника, можно воспользоваться одной из формул:
Для нахождения площади прямоугольника необходимо длину умножить на ширину:

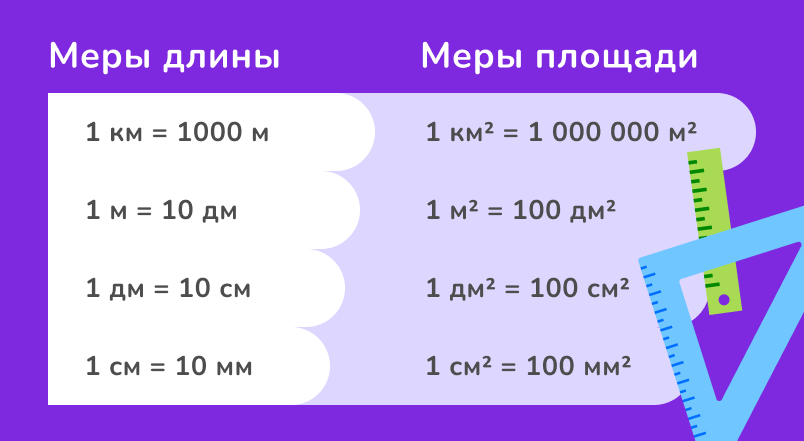
Если перимерт измеряется в сантиметрах, миллиметрах, дециметрах, километрах, то площадь в квадратных сантиметрах, квадратных миллиметрах, квадратных дециметрах, а также квадратных километрах.
Квадрат — прямоугольник, у которого все стороны равны. У квадрата также все углы прямые, а противоположные стороны параллельны.
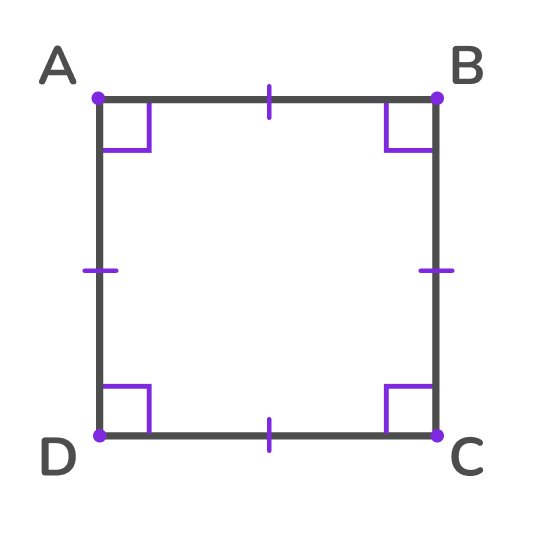
Благодаря равенству всех сторон периметр и площадь квадрата легко вычисляются.
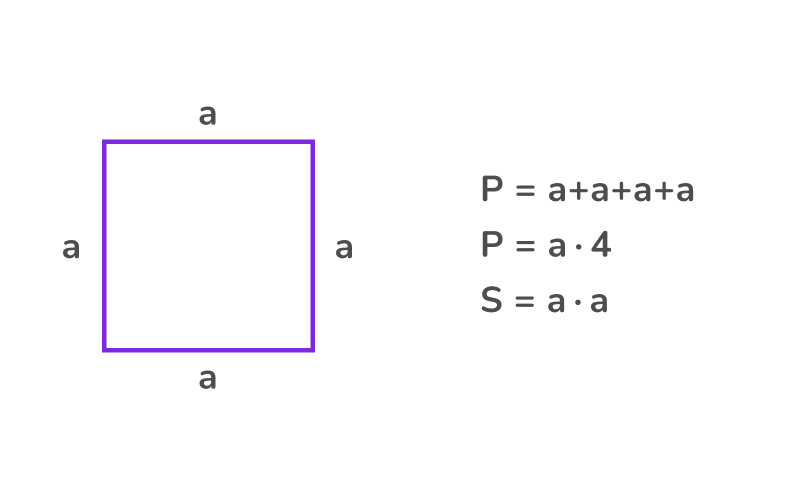
💡
В повседневной жизни нам часто приходится сталкиваться с предметами квадратной и прямоугольной формы, поэтому очень важно уметь вычислять их периметр и площадь. Тогда ответить на многие вопросы не составит труда.
Например, сколько ткани потребуется, чтобы сшить наволочку на подушку? Какую площадь занимает дверной проём? Какова длина и ширина забора вокруг земельного участка?

Треугольник
Геометрическая фигура, у которой три стороны и три вершины, — треугольник. Это простейший многоугольник.
В зависимости от соотношения длин сторон треугольники подразделяются на равносторонние, равнобедренные (две из трёх сторон равны по длине) и разносторонние. А также существует классификация треугольников по углам: остроугольные (все углы менее 90°), прямоугольные (один из углов 90°), тупоугольные (один из углов более 90°).
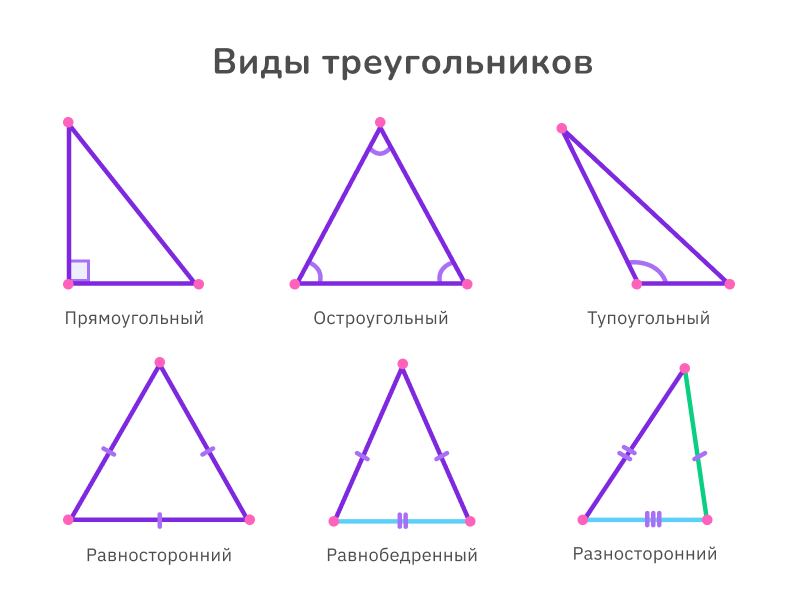
Треугольник — загадочная фигура, которая имеет множество интересных свойств. Например, в остроугольном треугольнике все углы равны 60°, а сумма всех углов любого треугольника равна 180°.
Для вычисления периметра треугольника нужно сложить длину всех его сторон:
Р = а + b + c.
В случае, если треугольник равносторонний, стоит воспользоваться формулой с умножением:
Р = a ⋅ 3.
🤍
Подробнее про периметр и площадь треугольника читайте в статьях ⤵
Круг и окружность
Окружность — это граница, замкнутая кривая линия, все точки которой находятся на одинаковом расстоянии от одной фиксированной точки — центра. Начертить окружности можно с помощью циркуля.
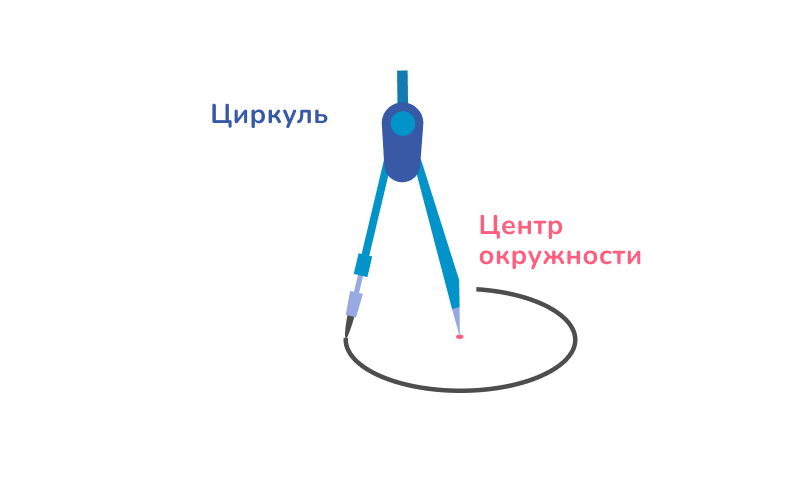
Отрезок, соединяющий любую точку окружности с центром, называется радиус. Его принято обозначать буквой R. Все радиусы равны между собой, так как по определению все точки окружности равноудалены от центра.
Отрезок, который соединяет две точки окружности и проходит через её центр, называется диаметр. Он обозначается буквой D. Чтобы узнать диаметр окружности, нужно сложить длину двух радиусов.
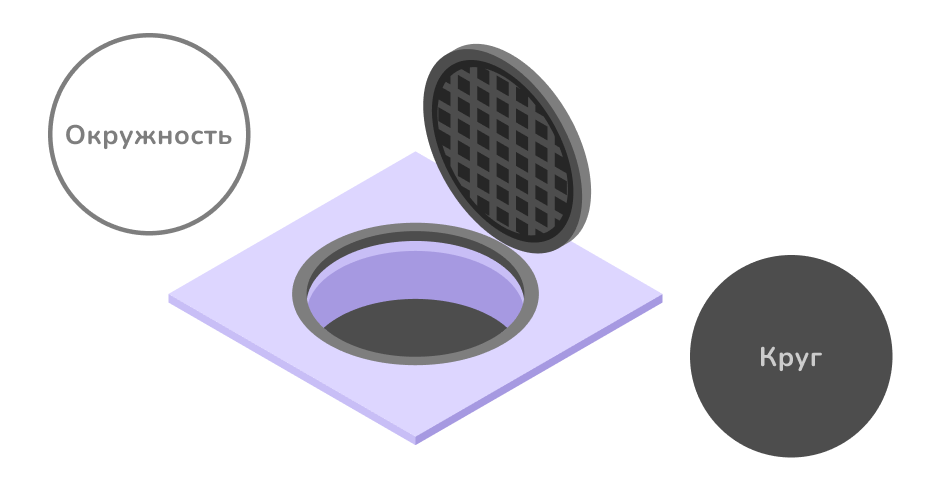
Часть плоскости, ограниченная окружностью, — круг. Он включает в себя саму окружность (границу) и все точки внутри неё. Круг обладает уникальной симметрией, как не поверни — он одинаков со всех сторон.
💡
Это свойство используют даже в бытовых целях. Например, круглые крышки люков и колодцев. Они сделаны именно такой формы, чтобы не провалиться независимо от того, как их повернуть.Тогда как квадратная, прямоугольная или овальная крышка может соскользнуть внутрь, если её вставить в отверстие по диагонали.
🤍
Правила вычисления площади круга и длины окружности не изучают в начальной школе. О них рассказываем в статье ⤵
Геометрические фигуры и геометрические тела
Все рассмотренные выше геометрические фигуры существуют в двухмерном измерении (2D). Они имеют длину и ширину, но не имеют толщины/высоты, т. е. они плоские.
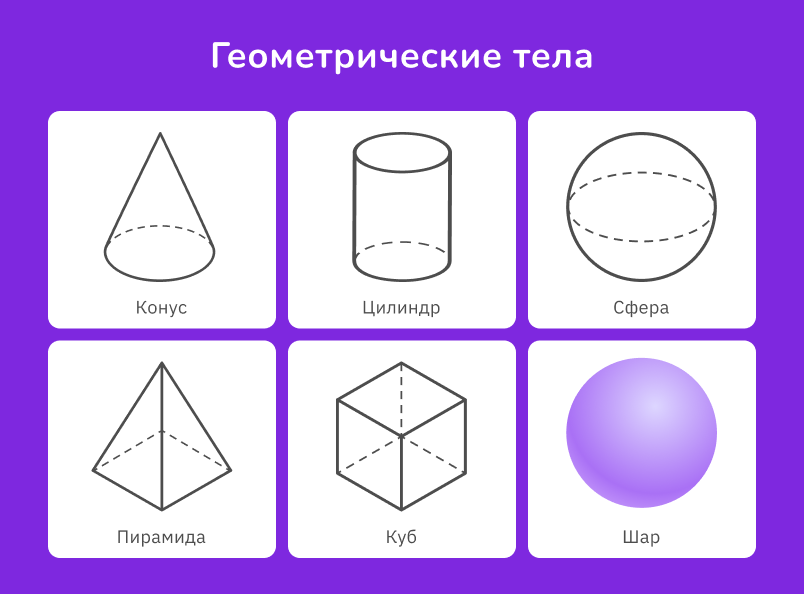
Объёмные фигуры, которые существуют в 3D измерении и имеют три характеристики: длину, ширину и высоту (толщину, глубину), называются геометрическими телами. Это реальные объекты, занимающие объём в пространстве. К ним относятся куб, шар, сфера, пирамида, цилиндр, а также конус.
💡
Геометрические фигуры составляют грани геометрических тел. Например, грань куба — квадрат, а грань пирамиды — треугольник.
Итак, нам удалось узнать, что:
- Точка — базовая геометрическая фигура, у которой нет характеристики размера.
- Прямая состоит из множества точек, но через две точки можно провести только одну прямую.
- Углы бывают прямые, острые,тупые и развёрнутые.
- У прямоугольника все углы прямые, а противоположные стороны равны. Прямоугольник, у которого все стороны равны, называется квадрат.
- Треугольник имеет три стороны и три вершины. Треугольники классифицируются по длине сторон и углам.
- Окружность — это замкнутая линия, точки которой равноудалены от её центра. Круг же — это часть плоскости, ограниченная окружностью. Если окружность — это забор, то круг — земля, которая находится внутри.
- Геометрические тела имеют объём, т. е. длину, ширину и высоту, тогда как у геометрических фигур есть только длина и ширина.
Если ребёнок испытывает затруднения в различении геометрических фигур, путается в их классификации и формулах вычисления периметра и площади, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия по математике.
Вводный урок по форме ниже — бесплатный!
 18
18
 3
3
 2
2








Комментарии 0