
Как найти дискриминант квадратного уравнения
В 8-м классе учащиеся начинают изучать квадратные уравнения и методы их решения. Одним из ключевых понятий в этой теме является диcкриминант. Понимание того, как находить дискриминант квадратного уравнения, помогает определить количество и тип корней уравнения, а также решить уравнение различными методами.
Понятие квадратного уравнения
Квадратное уравнение имеет форму:
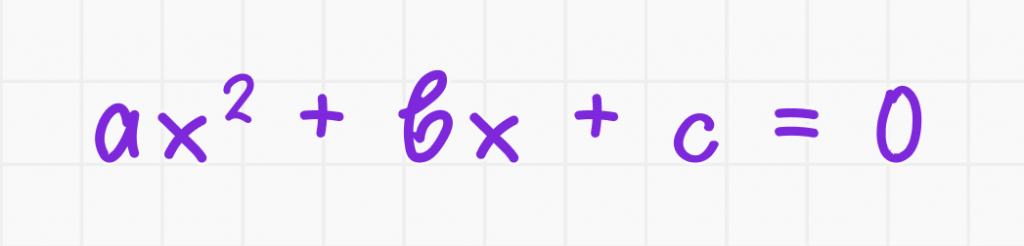
где a, b и c — коэффициенты, a ≠ 0. Это уравнение называется квадратным, поскольку наивысшая степень переменной x равна 2.
Понятие дискриминанта
Дискриминант квадратного уравнения — это числовая характеристика, которая помогает определить свойства его корней. Обозначается буквой D и вычисляется по следующей формуле:

Свойства
1. Если D > 0: у уравнения два различных действительных корня.
2. Eсли D = 0: у уравнения два одинаковых действительных корня (или один корень с кратностью 2).
3. Eсли D < 0: у уравнения нет действительных корней.
Как решать квадратные уравнения через дискриминант
Для решения квадратного уравнения используется следующая формула корней:
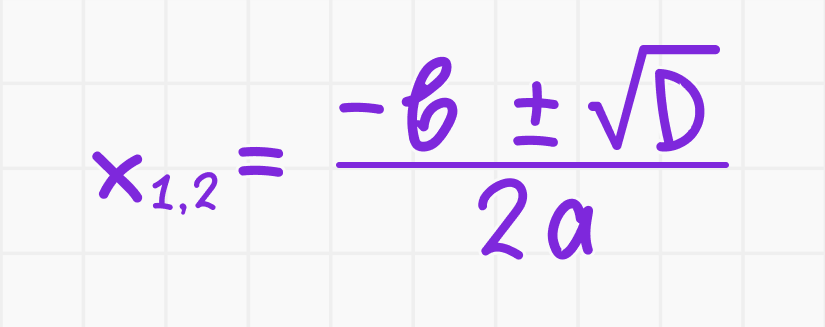
где ± означает, что существуют два возможных значения для корней, если дискриминант положительный.
Алгоритм решения квадратного уравнения через дискpиминант
1. Вычислите диcкриминант D:

2. Определите количество и тип корней в зависимости от знака диcкриминанта:
— Если D > 0, уравнение имеет два различных корня.
— Eсли D = 0, уравнение имеет один корень.
— Если D < 0, уравнение не имеет действительных корней.
3. Найдите корни уравнения с помощью формулы:
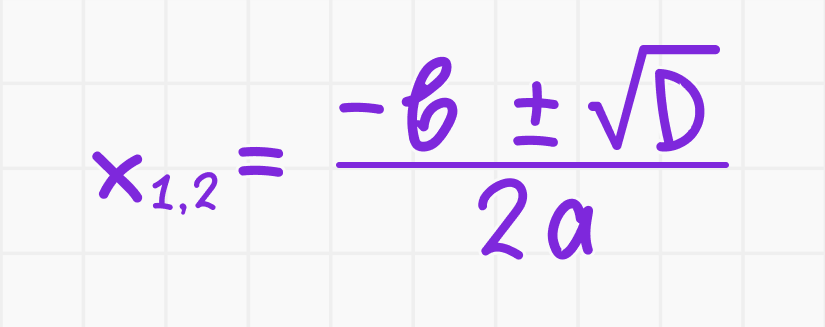

Понятие чётного дискриминанта
Если дискpиминант является квадратом целого числа (например, 1, 4, 9, 16 и т. д.), то он называется чётным. Это означает, что корни квадратного уравнения будут действительными числами, и уравнение можно решить с использованием корней квадратных чисел.
Как решать квадратные уравнения через чётный диcкpиминант
Процесс решения через чётный диcкриминант аналогичен общему случаю, но с тем, что D является квадратом какого-либо числа. Это упрощает вычисление корней, так как √D будет целым числом.
Алгоритм решения квадратного уравнения через чётный диcкриминант
1. Вычислите дискриминант D:

2. Проверьте, является ли D квадратом целого числа. Если да, то:
— Найдите корень из диcкриминанта: √D.
— Используйте формулу для нахождения корней уравнения:
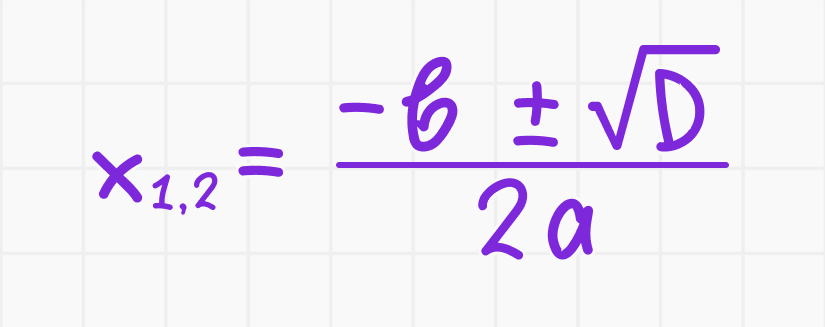
3. Запишите корни уравнения.
Решение квадратных уравнений через дискриминант
Рассмотрим пример.
1. Решите квадратное уравнение
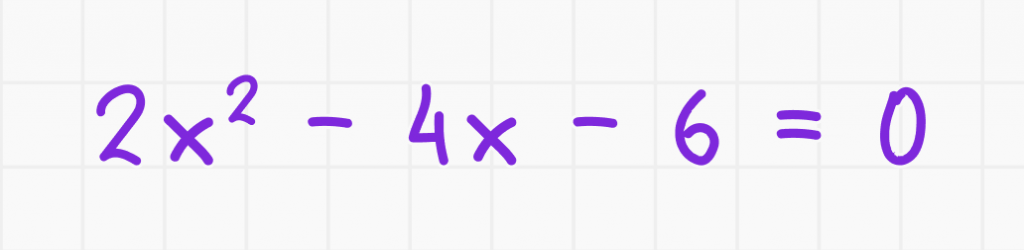
2. Найдите диcкриминант:

3. Определите корни:
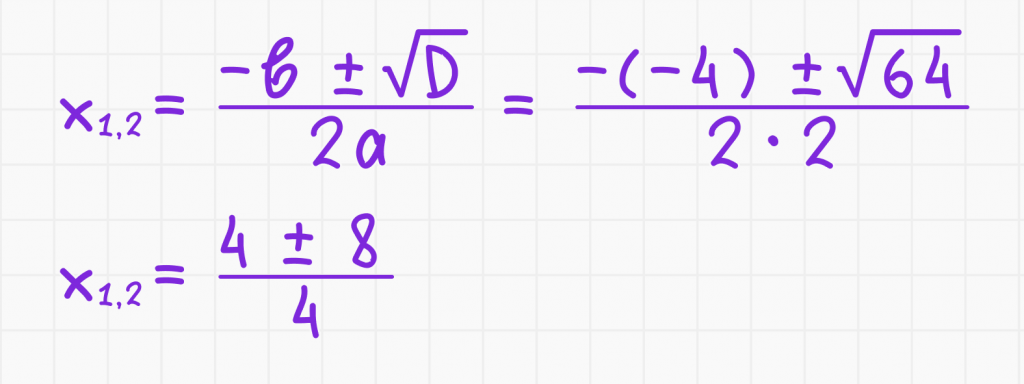
Корни будут:
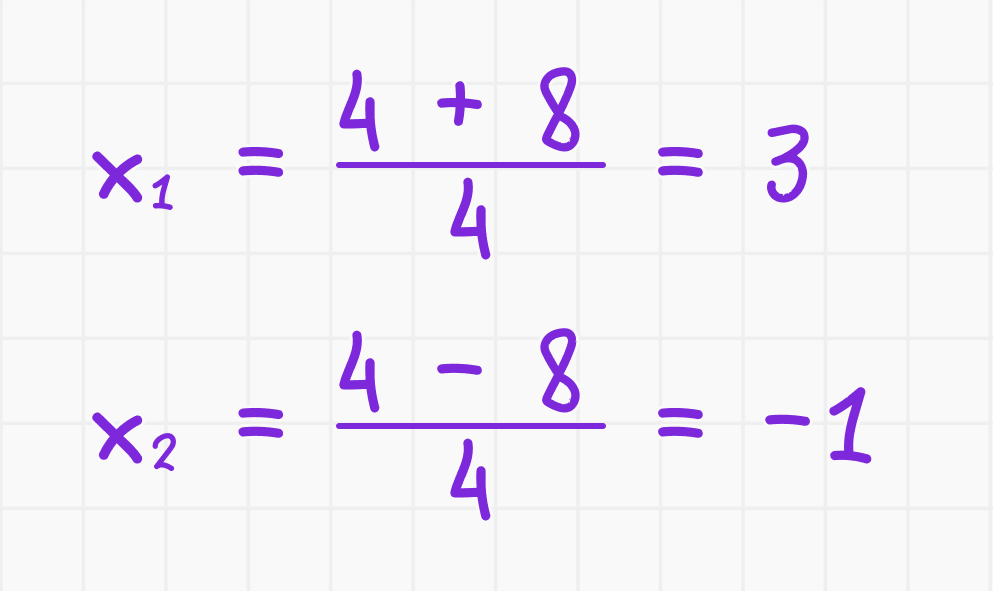
Диcкриминант квадратного уравнения играет ключевую роль в определении количества и типа корней. Знание того, как его вычислять и интерпретировать, позволяет эффективно решать квадратные уравнения и находить их корни. Овладение методами работы с диcкриминантом помогает в решении различных задач алгебры и в математике в целом.
Если ребёнок испытывает трудности в решении квадратных уравнений через дискриминант, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия.
Записаться на первый бесплатный урок можно по форме ниже 💜
Популярные статьи
 24
24
 7
7
 4
4








Комментарии 0