Тригонометрическая окружность: как пользоваться

Тригонометрическая окружность — это окружность с центром в начале координат и радиусом 1. А также её называют «числовая окружность» или «единичная окружность». В статье разберёмся, как ей пользоваться и зачем. 

Косинус и синус тригонометрической окружности

Таким образом, косинусом угла называется абсцисса точки на тригонометрической окружности, соответствующей этому углу. А синусом угла называется ордината точки на тригонометрической окружности, соответствующей этому углу.

Напомним, что абсцисса точки — это её координата на оси Х, а ордината точки — это её координата на оси Y.

Тригонометрическая окружность: основные точки

Рассмотрим основные точки на окружности. Напомним, что радианная мера — это мера измерения угла, где 1 радиан равен 180°. Соответственно, 0 радиан будет в точке 0°, радиан будет в точке 180°.

Аналогичным образом вычислим радианную меру углов для табличных значений. Будем учитывать, что точки верхней полуокружности принято записывать только через положительное направление движения по окружности. То есть против часовой стрелки. А точки нижней полуокружности — через отрицательное направление движения. То есть по часовой стрелке.

Получим следующие точки:

Ищем точку на окружности

Как же найти нужную точку на окружности?

Первый способ: значение угла в радианах необходимо перевести в градусную меру. Далее найти точку на окружности с учётом её периодичности — 360°.

Второй способ: искать в радианах. К примеру, найти точку 83. Это означает, что нужно отложить от начала 8 секторов, равных сектору с углом 3 или 60 градусов.

Выглядеть это будет следующим образом:

Ищем синус и косинус угла по окружности

Научимся определять синус и косинус угла по числовой окружности. Чтобы найти значение синуса или косинуса, необходимо от точки, соответствующей углу, опустить перпендикуляр на вертикальную ось для нахождения синуса и на горизонтальную ось для нахождения косинуса.

Для углов, отмеченных ранее, значения синуса и косинуса будут следующими: 

Немного изучив окружность, можно найти закономерность в значениях и со временем научиться их определять только по окружности. Тогда табличные данные уже будут не нужны.

Давай потренируемся: найдём синус и косинус угла 76.

По окружности найдём значения:

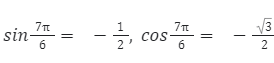
Стоит отметить, что этот способ подходит только для табличных значений.

Читайте также: Как делить в столбик: пошаговый алгоритм