Что такое квадратный корень

Квадратный корень — это одно из фундаментальных понятий математики, которое изучается в 8-м классе. Оно играет важную роль не только в школьной программе, но и в реальной жизни, например, при решении задач в физике, химии, экономике и других науках.

В этой статье мы разберём определение квадратного корня, его свойства, а также научимся выполнять различные операции с корнями: умножение, деление, возведение в степень, вынесение множителя и многое другое. 

Определение квадратного корня

📎 Квадратный корень из числа a — это число b, которое при возведении в квадрат даёт a.

b² = a

Однако важно помнить, что арифметический квадратный корень всегда является положительным числом.

Например:

Разница между квадратным корнем и арифметическим квадратным уравнением

📎 Квадратный корень — это математическая операция, которая позволяет найти число, квадрат которого равен заданному числу.

Пример:

Арифметическое квадратное уравнение — это уравнение вида x² = a, где a — заданное число. Решения такого уравнения могут быть как положительными, так и отрицательными.
Пример: x² = 9   ⇒   x = 3 или x = −3.

Запись иррациональных чисел с помощью квадратного корня

📎 Иррациональные числа — это числа, которые нельзя представить в виде обыкновенной дроби. Их часто записывают с помощью квадратного корня. Например:

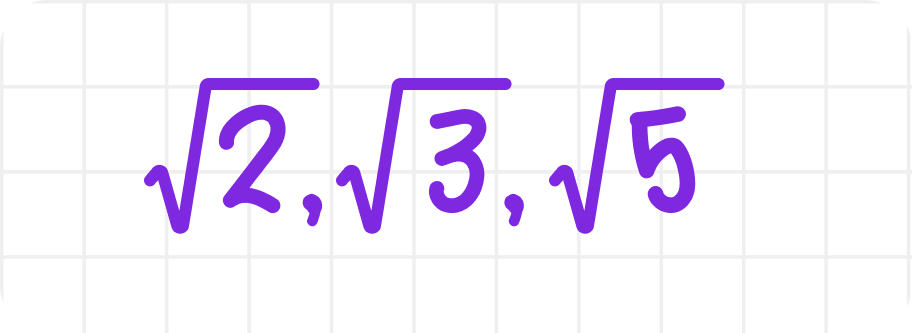
Эти числа называются иррациональными, потому что их десятичное представление бесконечно и непериодично. Например:

Извлечение квадратных корней

📎 Извлечение квадратного корня — это процесс нахождения числа, квадрат которого равен заданному числу. Если число является полным квадратом (например, 1, 4, 9, 16 и т. д.), то корень извлекается точно. Если число не является полным квадратом, то результат записывается в виде иррационального числа или приближённого значения.

Примеры извлечения корней ⤵︎

1. Полные квадраты:

2. Числа, которые не являются полными квадратами:

Методы извлечения корней ⤵︎

1. Использование таблицы квадратов
Таблица квадратов помогает быстро находить корни из чисел, которые являются полными квадратами. Например:

2. Разложение на множители

Для больших чисел можно использовать метод разложения на множители. Например:

3. Приближённое вычисление

Если число не является полным квадратом, можно найти приближённое значение корня. Например:

Свойства арифметического квадратного корня

1. Умножение арифметических корней

Корень из произведения двух чисел равен произведению корней этих чисел:

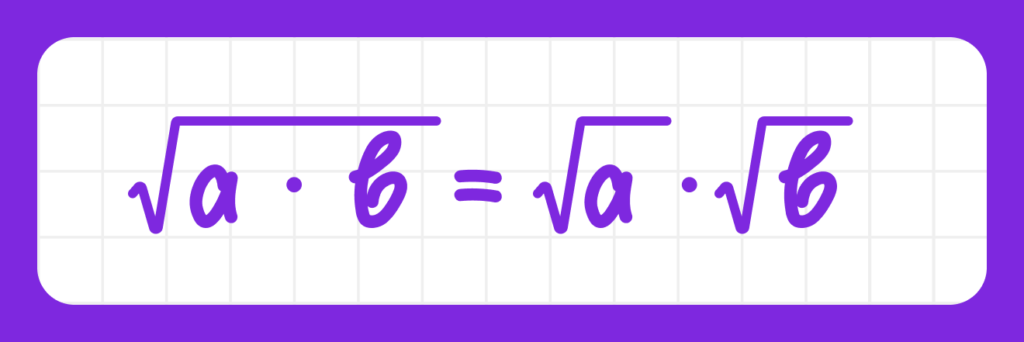
Примеры:

2. Деление арифметических корней

Корень из частного двух чисел равен частному корней этих чисел:

Примеры:

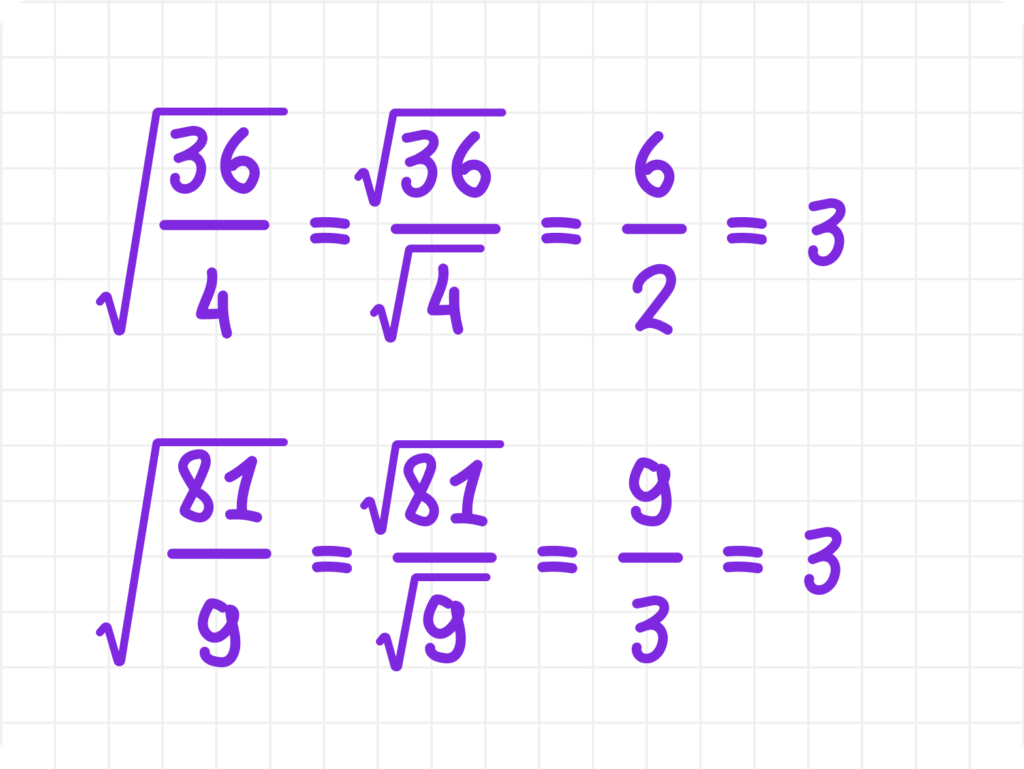
3. Возведение арифметических корней в степень и извлечение корня из степени

Корень, возведённый в степень, равен корню из числа, возведённого в ту же степень:

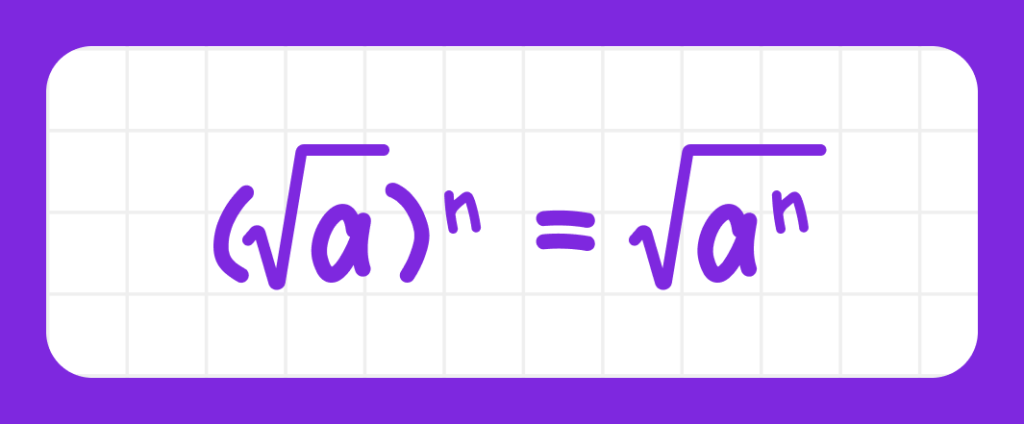
Примеры:

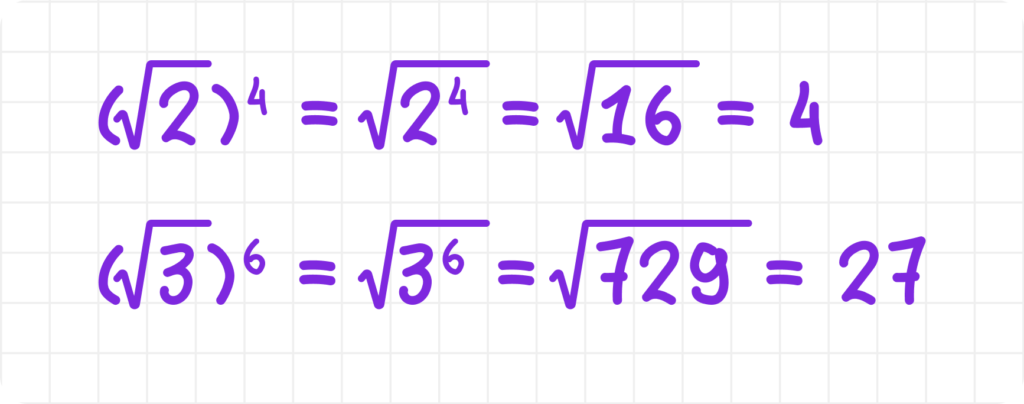
Корень из квадрата числа равен модулю этого числа:

Примеры:

4. Вынесение множителя из-под знака корня

Если под корнем есть множители, которые являются полными квадратами, их можно вынести:

Примеры:

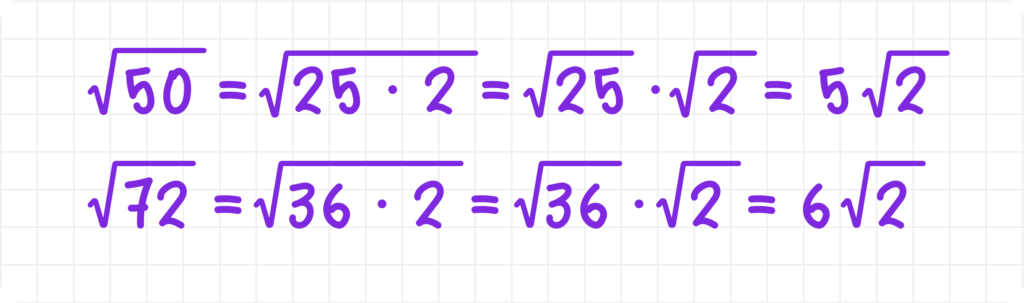
5. Внесение множителя под знак корня

Если перед корнем стоит множитель, его можно внести под знак корня, возведя его в квадрат:

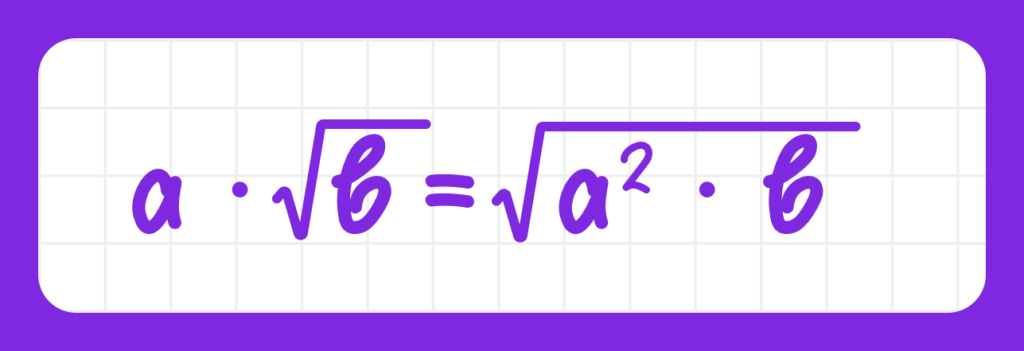
Примеры:

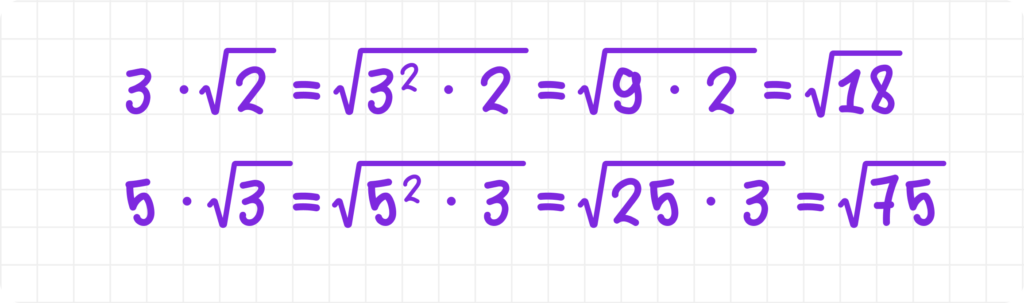
Сравнение квадратных корней

Чтобы сравнить два квадратных корня, нужно сравнить их подкоренные выражения. Если подкоренное выражение одного корня больше, то и сам корень больше:

Примеры:

Извлечение квадратного корня из большого числа

Извлечение квадратного корня из большого числа может показаться сложной задачей, но с использованием правильных методов это становится доступным. Рассмотрим несколько способов, которые помогут упростить процесс.

1. Метод разложения на множители

Если число можно разложить на произведение множителей, среди которых есть полные квадраты, то корень извлекается поэтапно:

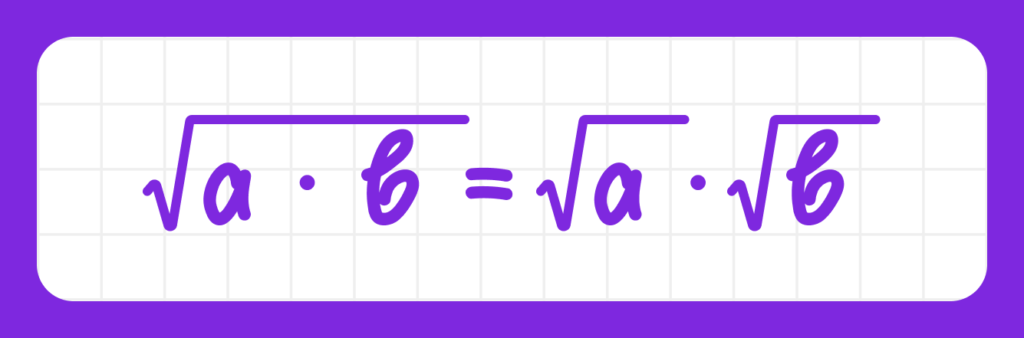
Примеры:

2. Использование таблицы квадратов

📎 Таблица квадратов — это удобный инструмент для быстрого нахождения корней из чисел, которые являются полными квадратами. Если число входит в таблицу, корень извлекается точно.

Примеры:

Таблица квадратов от 0 до 100 ⤵︎

3. Приближённое вычисление

Если число не является полным квадратом, то корень можно найти приближённо. Для этого подбираются ближайшие полные квадраты и выполняется оценка.

Примеры:

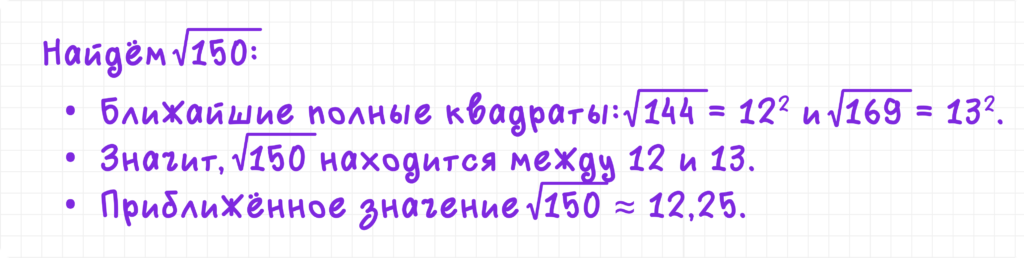
Решение примеров с квадратными корнями

1. Упростите выражение:

Решение ⤵︎

Разложим каждое подкоренное выражение на множители, выделяя полные квадраты:

Подставим упрощённые значения в выражение:

2. Найдите значение выражения:

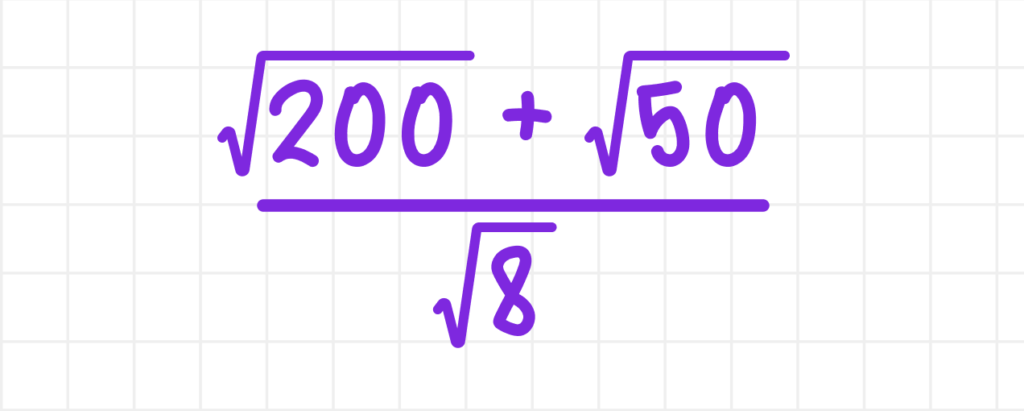
Решение ⤵︎

Упростим корни в числителе, выделяя полные квадраты:

Подставим упрощённые значения в числитель:

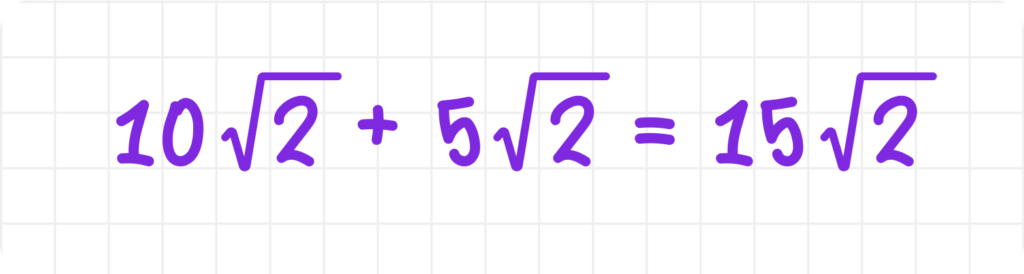
Упростим знаменатель:

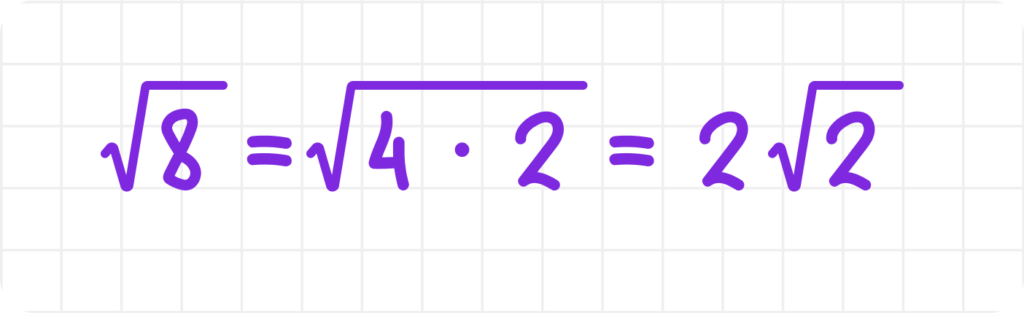
Разделим числитель на знаменатель:

3. Упростите выражение:

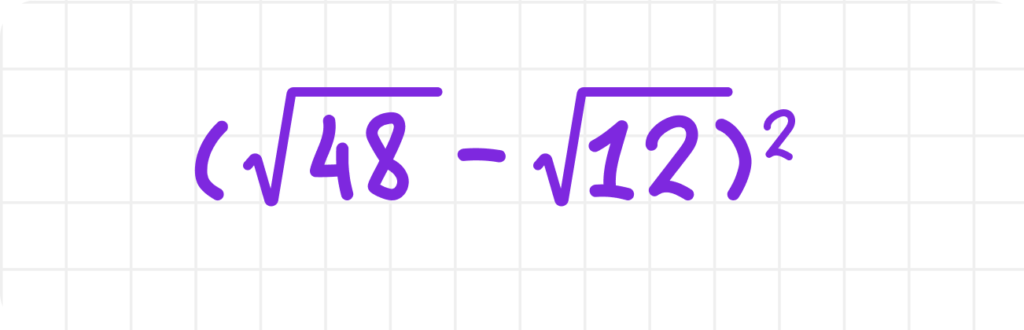
Решение ⤵︎

Раскроем квадрат разности по формуле:

Вычислим каждый член:

Упростим произведение под корнем:

Подставим значения в выражение:

48 − 2 ⋅ 24 + 12 = 48 − 48 + 12 = 12.

Ответ: 12.

---

Мы разобрали, что такое квадратный корень, его свойства и способы работы с ним. Эти знания помогут вам решать задачи, связанные с квадратными корнями, и лучше понимать математические концепции.

Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к нашим репетиторам!