Как исследовать функции

Исследовать поведение функции по построенному графику не так сложно. А вот можно ли исследовать функцию аналитически, без графика? Можно! И сейчас мы покажем, как это сделать.

Аналитическое исследование функции

Пример

Рассмотрим подробнее каждый из пунктов сразу на примере.

Пусть дана функция:

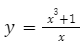
1. Область определения — это все допустимые значения х.

Так как в данной функции есть переменная в знаменателе, укажем, что он не равен нулю: x ≠ 0. Тогда х может принимать значения D = (-∞; 0) ∪ (0; +∞).

2. Используем непрерывность с помощью пределов. Выше мы нашли, что x ≠ 0.

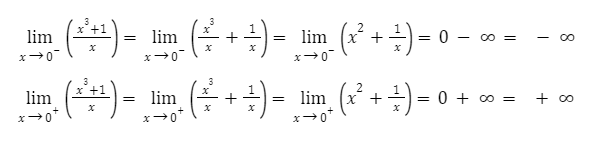
Следовательно, функция имеет разрыв в точке x = 0.

3. Чётность функции определяется свойством: f (-x) = f (x), нечётность  функции определяется свойством: f (-x) = -f (x).

В нашем случае функция не симметрична, поэтому можем утверждать, что является ни чётной, ни нечётной.

4. Нули функции — это точки пересечения графика с ОХ. То есть значения x функции, при которых у = 0.

Найдём для нашего примера:

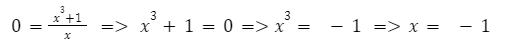
График пересекает ось ОХ в точке (-1; 0).

5. Монотонность исследуется с помощью производной. 

Рассмотрим второй вариант, найдём производную данной функции:

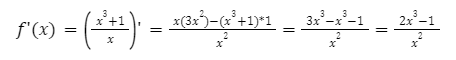
Приравняем её к 0 и найдём корни:

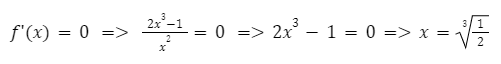
При помощи интервалов определим промежутки возрастания и убывания:

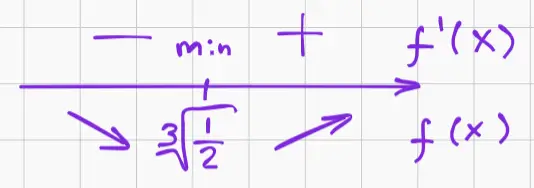
Таким образом, функция убывает на промежутке:

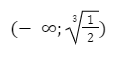
и возрастает на промежутке:

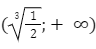
Данная точка:

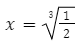
является точкой минимума, а точек максимума у данной фyнкции не будет.

6. Исследуем асимптоты, используя пределы:

Исследуем вертикальную асимптоту. Выше мы нашли, что x ≠ 0.

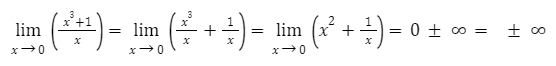
Следовательно, x = 0 является вертикальной асимптотой.

Исследуем горизонтальную асимптоту:

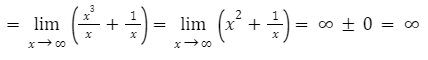
Горизонтальной асимптоты нет.

Исследуем наклонные асимптоты:

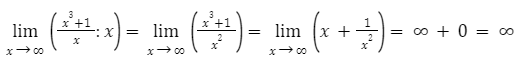
Наклонных асимптот нет.

По полученным данным схематично построим график:

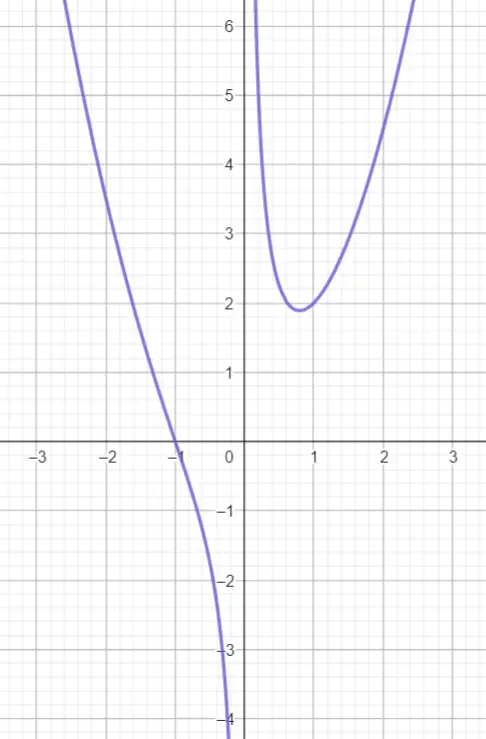
7. Область значений — все возможные значения у, которые может принимать заданная функция.

В данном примере ограничений сверху или снизу нет, следовательно: E = (-∞; +∞).

Итак, мы исследовали функцию без построения, только аналитически, и уже по полученному словесному описанию можем построить график или приблизительный макет. Именно поэтому важно уметь исследовать фyнкции. Мы разобрали теорию на простом примере, но с этими знаниями вы сможете исследовать любую функцию.

📌 Читайте также: Как найти периметр и площадь прямоугольника и квадрата