Действия над векторами

Для начала вспомним, что такое вектор и какие виды векторов существуют. А потом разберём, какие действия можно производить над векторами.

Что такое вектор

Вектор — это отрезок, для которого определено начало и конец. То есть отрезок, имеющий направление.

Векторы бывают коллинеарные — лежащие на параллельных прямых или на одной прямой, и неколлинеарные. Коллинеарные векторы могут быть сонаправлены (в одном направлении) и противоположно направлены (в разных направлениях).

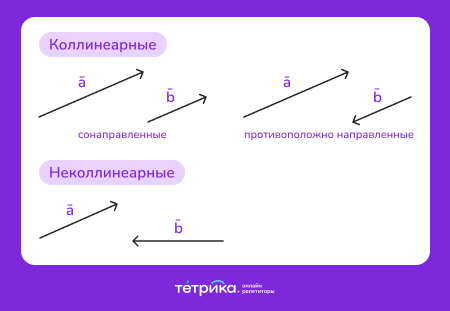
Далее подробнее поговорим о том, какие действия можно производить над векторами.

Сложение векторов 

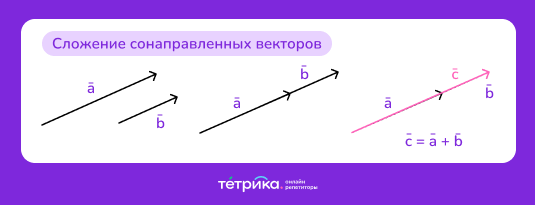
Сложение векторов производится по разным правилам. Если векторы коллинеарны и сонаправлены, тогда располагаем их таким образом, чтобы начало второго вектора совпадало с концом первого. Тогда результирующий вектор будет направлен прямо вдоль складываемых векторов. То есть его начало будет совпадать с началом первого, а конец — с концом второго.

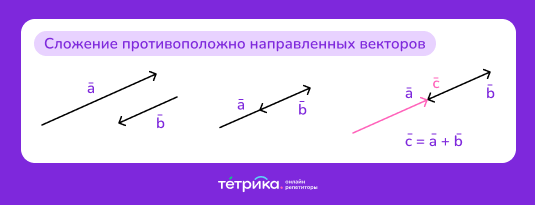
Если же векторы коллинеарны и противоположно направлены, тогда располагаем их по тому же правилу, что и в случае с сонаправленными. Только теперь начало результирующего вектора будет совпадать с началом большего из них, а конец — с концом меньшего.

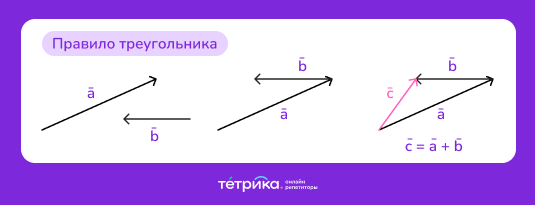
Сложение неколлинеарных векторов можно выполнить по правилу треугольника. Первым шагом делаем то же самое: располагаем векторы так, чтобы начало второго совпадало с концом первого из них (определение первого и второго не столь важно). И проводим результирующий вектор, начало которого совпадает с началом первого, а конец — с концом второго (здесь порядок векторов менять нельзя). 

Другой способ — правило параллелограмма. Чтобы сложить два вектора по правилу параллелограмма, необходимо расположить их так, чтобы начала векторов совпадали. После — достраиваем до параллелограмма, проводя параллельные и равные отрезки, и затем проводим результирующий вектор (диагональ параллелограмма, выходящая из этой же точки, что и векторы).

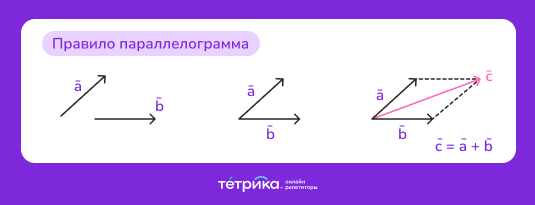
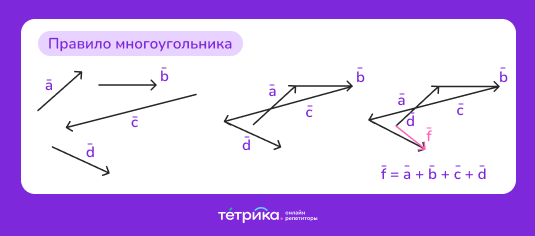
А если же необходимо сложить несколько векторов, то сделать это можно по правилу многоугольника. Для этого векторы поочерёдно располагаем таким образом, чтобы начало последующего вектора совпадало с концом предыдущего. Получим последовательность векторов. Результирующий вектор имеет начало в начале первого вектора, а конец — в конце последнего вектора.

Вычитание векторов

Разность двух векторов a и b — это вектор, сумма которого с вектором b даёт вектор a. Соединяем начала векторов, тогда начало вектора разности совпадёт с концом вычитаемого вектора, а конец — с концом уменьшаемого.  При построении это будет выглядеть так:

Умножение вектора на число

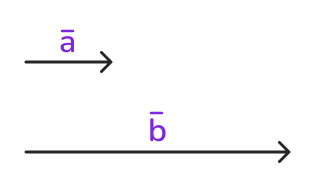
Вектор b — есть произведение вектора a на число k. Тогда b=a * k,  и при этом:

1. Векторы a и b сонаправлены, если k положительно: b=a * 3

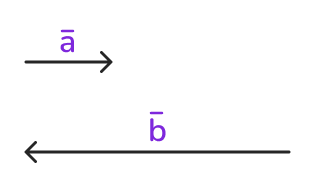
2. Векторы a и b противоположно направлены, если k отрицательно: b=a * (-3)

Читайте также: Как найти площадь треугольника