Уравнения с модулем: как решать

Напомним, что модуль — это неотрицательное число, обозначающее расстояние между началом координат и подмодульным выражением. И при возникновении модуля в уравнении необходимо уметь правильно его раскрыть. В этой статье мы как раз и научимся правильно решать уравнения с модулем.

Как решать уравнения с модулем без переменной внутри

Если модуль внутри себя содержит только число, то раскрывается он следующим образом:

| k | = k

| -k | = k

k — положительное число.

Например: x + |-4| = 0 => x + 4 = 0 => x= -4

Kак решать уравнения с модулем с переменной внутри

Как правило, сложности появляются при возникновении неизвестной переменной под знаком модуля, потому что переменная может принимать любые значения, следовательно, невозможно определить исход.

Например: | 4x — 1 | = 7

В таком случае раскрытие модуля производится так:

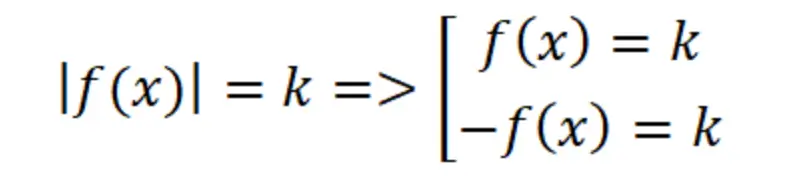
Иными словами, одно уравнение превращается в два, но уже без модуля, решение которых мы легко можем найти.

Посмотрим на примере:

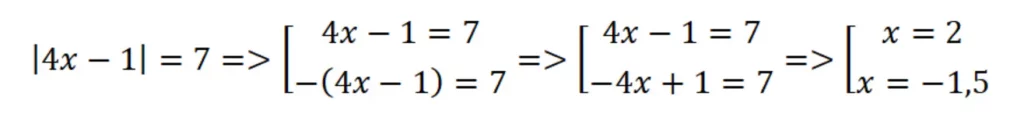
Получили два корня, при подстановке которых получим верное уравнение.

Дополнительно рассмотрим ситуацию, когда модуль приравнивается к некой функции, содержащей переменную.

Уравнение с модулем будет следующее: |x| = 3x — 5. 

Здесь необходимо предусмотреть условие, что модуль неотрицателен, следовательно, не может равняться отрицательному значению:

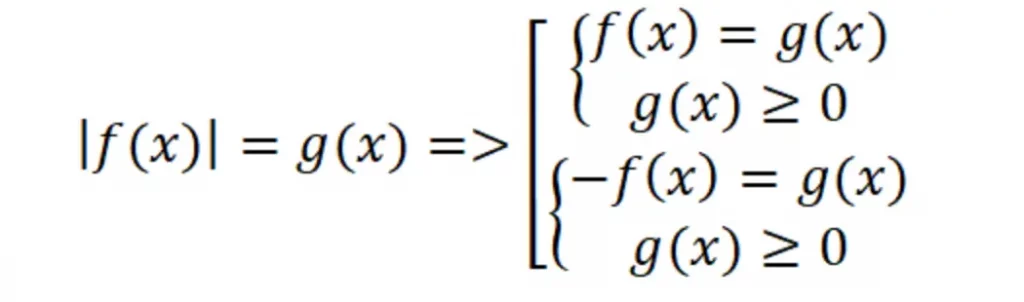
На нашем примере:

А значит подойдёт только корень x = 2,5.

🖇️ Читайте также: Как научиться быстро решать уравнения