Как решать задачи с процентами

Проценты — это способ выразить долю или часть числа в виде части от ста. Понимание процентов важно не только для школьной математики в 5–9-х классах, но и для решения практических задач в повседневной жизни, таких как вычисление скидок, налогов, процентов по кредитам и инвестициям. В этой статье мы подробно рассмотрим, как решать задачи с процентами, используя различные методы и формулы.

Основные понятия

Для решения задач с процентами нужно знать несколько ключевых понятий:

1. Процент — это часть целого, выраженная в сотых долях. 1 процент (1%) равен 1/100 (или 0,01) от целого.

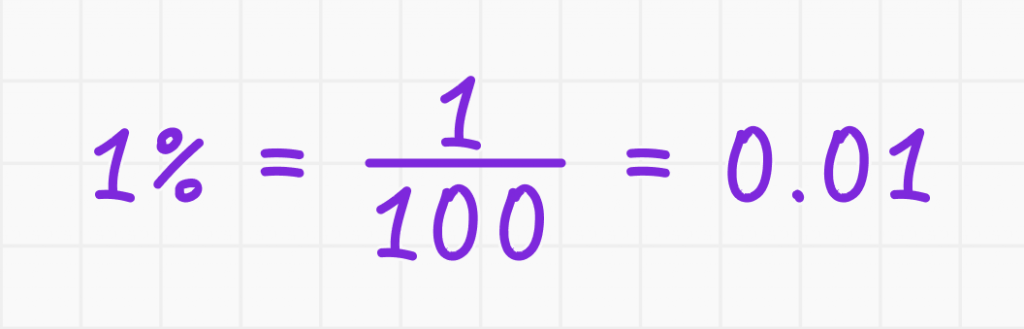
1. Процентное отношение — это отношение одного числа к другому, выраженное в процентах.
2. Процентное увеличение или уменьшение — изменение величины на определённый процент.

Виды задач на проценты

Задачи с процентами можно разделить на несколько типов. Рассмотрим каждый из них с примерами:

1. Нахождение процента от числа

В этой задаче нужно вычислить, сколько процентов от заданного числа составляют другие величины.

Пример 1:

Как найти 25% от числа 80?

1. Определите значение процента: 25%.
2. Преобразуйте значение процента в дробь: 

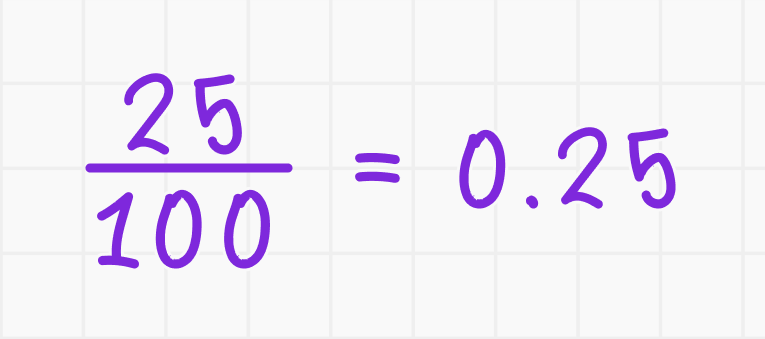
3. Умножьте на число: 0,25 ∙ 80 = 20.

Ответ: 25% от числа 80 — это 20.

Пример 2:

Сколько составляет 10% от 1 500 рублей?

1. Преобразуйте процент в дробь: 

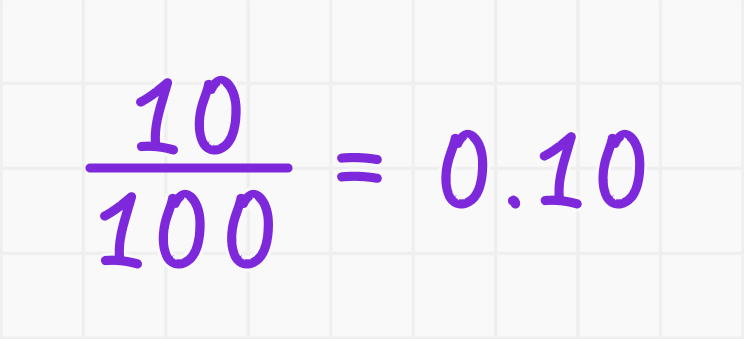
2. Умножьте: 0,10 ∙ 1 500 = 150.

Ответ: 10% от 1 500 рублей — это 150 рублей.

2. Нахождение числа по его проценту

В этой задаче нужно определить исходное число, если известен его процент.

Пример 1:

Если 30% числа равно 45, какое это число?

1. Определите значение процента: 30%.
2. Используйте формулу: 

Ответ: исходное число равно 150.

Пример 2:

Если 75% числа составляет 90, как найти это число?

1. Преобразуйте процент в дробь: 75% = 0,75.
2. Используйте формулу: 

Ответ: исходное число равно 120.

3. Нахождение процентного соотношения двух чисел

Для этой задачи нужно вычислить, какой процент одно число составляет от другого.

Пример 1:

Какой процент составляет число 50 от числа 200?

1. Используйте формулу: 

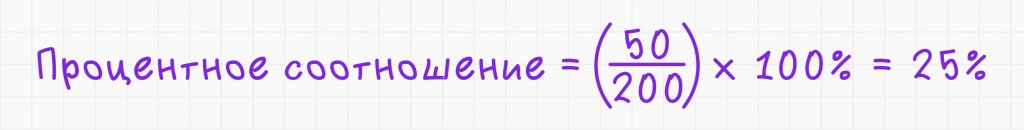
Ответ: число 50 составляет 25% от числа 200.

Пример 2:

Какой процент составляет число 30 составляет от 120?

1. Используйте формулу: 

Ответ: число 30 составляет 25% от числа 120.

4. Увеличение или уменьшение числа на процент

В этой задаче нужно определить новое значение числа после его увеличения или уменьшения на заданный процент.

Пример 1 (увеличение):

Какое число получится, если увеличить 200 на 15%?

1. Используйте формулу: 

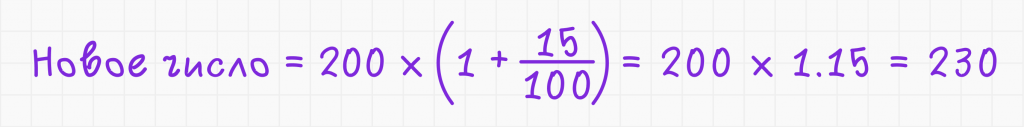
Ответ: число 230.

Пример 2 (уменьшение):

Какое число получится, если уменьшить 200 на 10%?

1. Используйте формулу:

Ответ: число 180.

Простые и сложные проценты

Проценты — это важная часть финансовых расчётов, и понимание разницы между простыми и сложными процентами может помочь вам принимать более обоснованные финансовые решения. Рассмотрим эти два типа процентов подробнее.

Простые проценты

Определение. Простые проценты вычисляются только на начальную сумму (основную сумму) за каждый период времени. Это означает, что процент начисляется на исходную сумму, а не на уже начисленные проценты.

Формула простых процентов:

I = P ∙ r ∙ t,

где:

1. I — сумма процентов;
2. P — начальная сумма (основная сумма);
3. r — годовая процентная ставка (в десятичном виде);
4. t — время в годах.

Пример задачи:

Вы вложили 10 000 рублей под 5% годовых простых процентов на 3 года. Сколько процентов вы получите за это время?

Решение:

1. Определим сумму процентов по формуле простых процентов:
I = P ∙ r ∙ t = 10 000 ∙ 0,05 ∙ 3 = 1 500 рублей.

За 3 года вы получите 1 500 рублей в виде процентов.

Ответ: сумма процентов составит 1 500 рублей.

Сложные проценты

Определение. Сложные проценты начисляются не только на начальную сумму, но и на ранее начисленные проценты. Это означает, что проценты рассчитываются на каждый новый период, учитывая ранее начисленные проценты, что приводит к эффекту «процентов на проценты».

Формула сложных процентов:

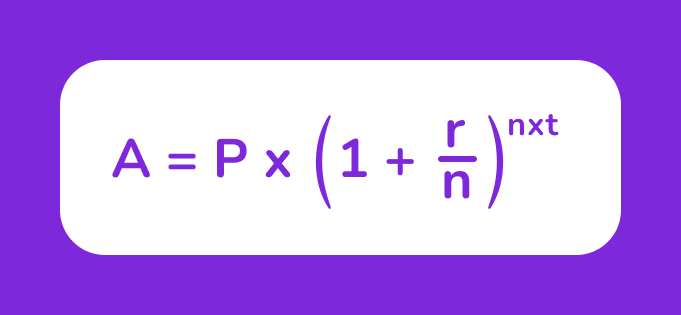
где:

1. A — конечная сумма (основная сумма плюс проценты);
2. P — начальная сумма (основная сумма);
3. r — годовая процентная ставка (в десятичном виде);
4. n — количество начислений процентов в год;
5. t — время в годах.

Пример задачи:

Вы вложили 10 000 рублей под 5% годовых сложных процентов, которые начисляются ежемесячно, на 3 года. Какова будет конечная сумма через 3 года?

Решение:

1. Преобразуем годовую процентную ставку в месячную и количество начислений в год: r = 0,05, n = 12 (ежемесячное начисление).
2. Подставьте значения в формулу:

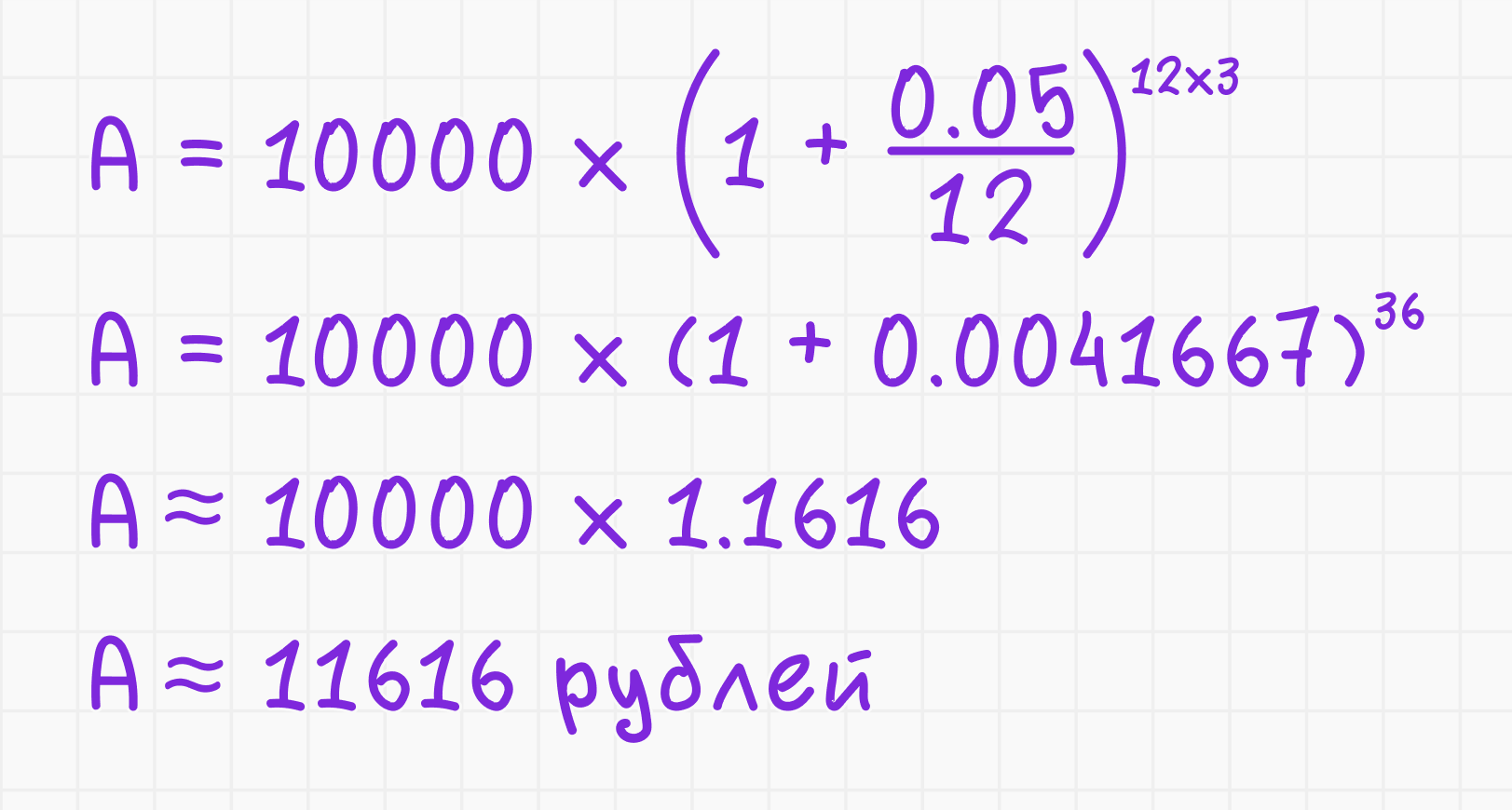
Конечная сумма через 3 года составит примерно 11 616 рублей.

Ответ: конечная сумма через 3 года составит 11 616 рублей.

Решение задач с помощью составления пропорции

Пропорция — это равенство двух дробей, которое используется для нахождения процентов и сравнения величин.

Пример 1:

В магазине была скидка 20% на товар, который стоил 1 200 рублей. Какова новая цена товара?

1. Составим пропорцию: 

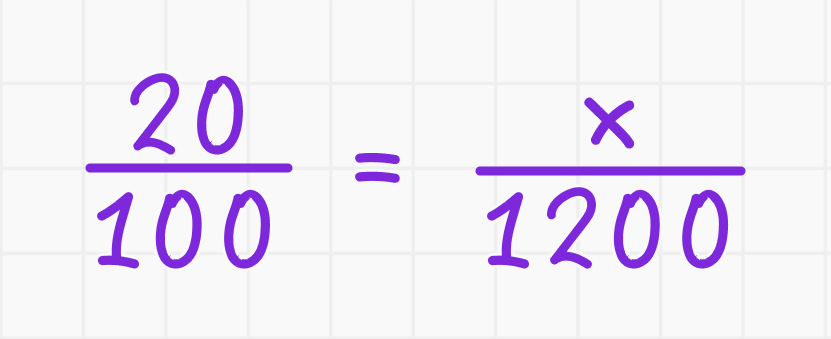
2. Решим пропорцию: 

3. Вычисляем новую цену: 1 200 — 240 = 960 рублей.

Ответ: новая цена товара составит 960 рублей.

Пример 2:

Если процентная ставка по депозиту составляет 8%, а сумма вклада равна 2 500 рублей, сколько процентов составит накопленная сумма за один год?

1. Используйте формулу:

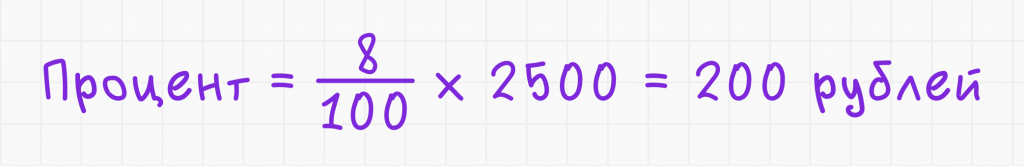
Ответ: проценты за один год составят 200 рублей.

Решение задач с помощью соотношения чисел

Для решения задач с помощью соотношения чисел, нужно определить процентное соотношение между числами и использовать это для вычисления неизвестных величин.

Пример 1:

Если число А составляет 30% от числа В, и число В равно 80, найдите число А.

1. Используйте формулу: 

Ответ: число А равно 24.

Пример 2:

Число B составляет 45% от числа C, и число C равно 200. Найдите число B.

1. Используйте формулу: 

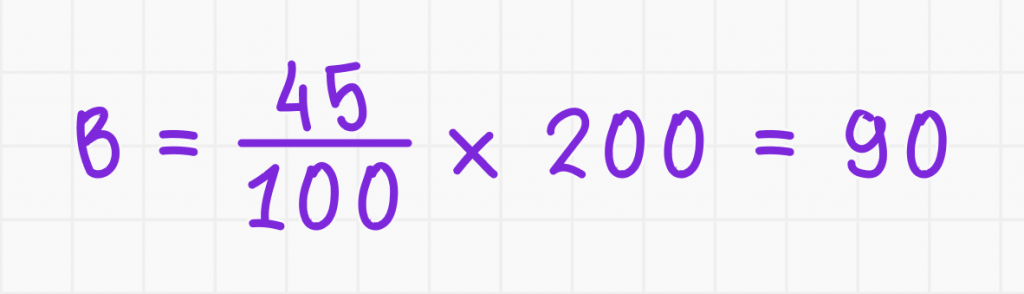
Ответ: число B равно 90.

Практика решения задач на проценты

Задача 1. В магазине была скидка 25% на товар, который стоил 1 200 рублей. Какова новая цена товара?
Решение:

1. Сначала найдём скидку: 25% ∙ 1200 = 25/100 ∙ 1200 = 300 рублей.
2. Новая цена: 1 200 — 300 = 900 рублей.

Ответ: новая цена товара составляет 900 рублей.

Задача 2. Вы получили 15% прибыли от инвестиций в 5 000 рублей. Какова сумма прибыли?
Решение:

1. Используем формулу:

Ответ: сумма прибыли составляет 750 рублей.

Задача 3. Расходы выросли на 12% и составляют теперь 5 600 рублей. Каковы были исходные расходы?
Решение:

1. Найдём исходные расходы:

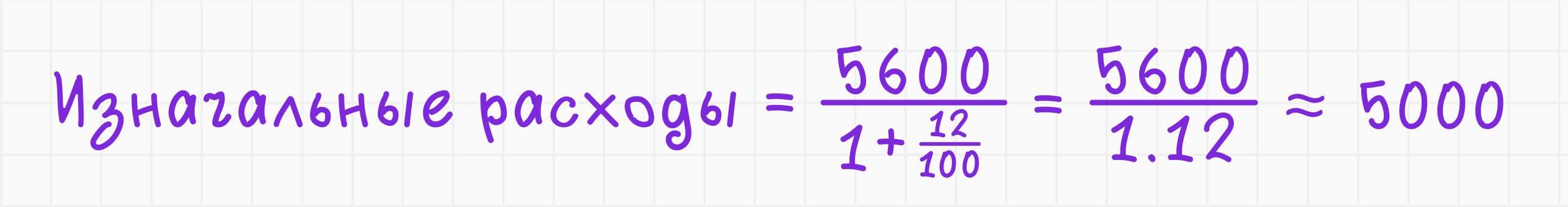
Ответ: изначальные расходы составляли 5 000 рублей.

Задача 4. Зарплата увеличилась на 8% и составила 43 200 рублей. Какая была зарплата до увеличения?
Решение:

1. Найдём исходную зарплату:

Ответ: изначальная зарплата составляла 40 000 рублей.

Задача 5. Какой процент числа 240 составляет 72?
Решение:

1. Используем формулу:

Ответ: 72 составляет 30% от 240.

Задача 6. Цена товара увеличилась с 2 500 рублей до 3 000 рублей. На сколько процентов увеличилась цена?
Решение:

1. Определим изменение цены: 

Изменение = Новая цена — Старая цена = 3 000 — 2 500 = 500 рублей

1. Найдём процентное увеличение:

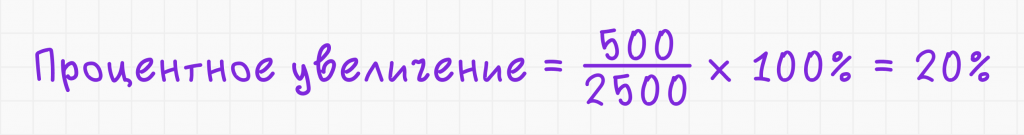
Ответ: цена увеличилась на 20%.

---

Задачи с процентами могут показаться сложными, но знание основных понятий и формул помогает их легко решать. Использование пропорций, соотношений чисел и формул для простых и сложных процентов позволит вам эффективно решать задачи и применять эти знания в реальной жизни. 

Если ребёнок испытывает трудности в решении задач на проценты, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия 🌸

Первый урок с опытным репетитором — бесплатно, записывайтесь по форме ниже ⇘