Вписанная и описанная окружность

Вписанная и описанная окружность играют важную роль в геометри, так как они устанавливают связь между многоугольниками и их геометрическими характеристиками. Эти понятия изучаются в 8-м классе и помогают решать задачи на вычисление площадей, углов и других параметров фигур.

Оба типа окружностей широко применяются в задачах геометрии, особенно при работе с треугольниками и четырёхугольниками, так как позволяют находить взаимосвязи между элементами фигур и использовать универсальные формулы для расчётов. В статье изучим их подробнее.

Вписанная окружность 

📎 Вписанная окружность — это окружность, которая касается всех сторон многоугольника. Центр такой окружности называется инцентром , а радиус — радиусом вписанной окружности.

Многоугольник, в который можно вписать окружность, называется описанным многоугольником.

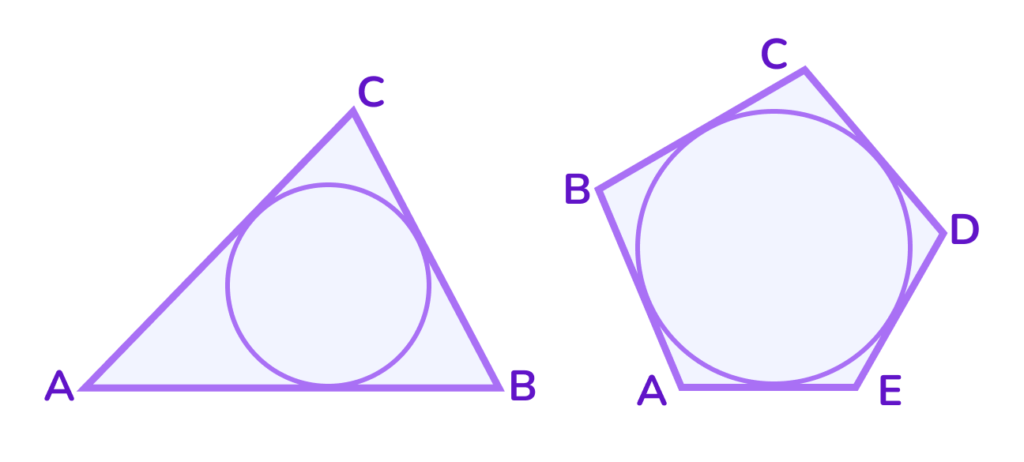
Окружность может быть вписана не в любой многоугольник. Для этого необходимо выполнение определённых условий ⤵︎

1) В треугольник окружность может быть вписана всегда, независимо от его типа (остроугольный, тупоугольный или прямоугольный).

2) В четырёхугольник окружность можно вписать только при условии, что суммы длин его противоположных сторон равны. Примеры таких четырёхугольников: ромб, квадрат и некоторые другие.

3) В правильные многоугольники (например, правильный треугольник, квадрат, пятиугольник) окружность также всегда можно вписать.

Свойства и формулы для вписанной окружности 

📌 Свойства вписанной окружности и треугольника

1. В любой треугольник можно вписать окружность, и только одну. Это одно из важнейших свойств треугольников: для любого треугольника существует единственная окружность, которая касается всех его сторон.

2. Центр вписанной окружности (инцентр) совпадает с точкой пересечения биссектрис углов треугольника.

3. Окружность касается каждой стороны треугольника в одной точке. Отрезки касательных, проведённых из одной вершины треугольника к точкам касания, равны между собой.

4. Радиус вписанной окружности перпендикулярен стороне треугольника в точке касания.

📌 Формулы вписанной окружности и треугольника

1. Радиус вписанной окружности через площадь и полупериметр треугольника:

r = S / p, где:

1. r — радиус вписанной окружности;
2. S — площадь треугольника;
3. p — полупериметр (p = (a + b + c) / 2).

2. Радиус вписанной окружности для прямоугольного треугольника:

r = (a + b — c) / 2

где a и b — катеты, c — гипотенуза.

3. Радиус вписанной окружности для равностороннего треугольника:

r = a / (2 ⋅ √3)

где a — сторона треугольника.

4. Площадь треугольника через радиус вписанной окружности:

S = r ⋅ p, где:

1. S — площадь треугольника;
2. r — радиус вписанной окружности;
3. p — полупериметр.

5. Отрезки касательных для треугольника:

x = p — a, y = p — b, z = p — c, где:

1. x, y, z — длины отрезков касательных;
2. p — полупериметр;
3. a, b, c — стороны треугольника.

📌 Формулы вписанной окружности и четырёхугольника

1. Окружность можно вписать в четырёхугольник, если суммы длин его противоположных сторон равны:

a + c = b + d

где a, b, c, d — длины сторон четырёхугольника.

2. Радиус вписанной окружности через площадь и полупериметр:

r = S / p, где:

1. r — радиус вписанной окружности;
2. S — площадь четырёхугольника;
3. p — полупериметр (p = (a + b + c + d) / 2).

3. Радиус вписанной окружности для квадрата:

r = a / 2,

где a — сторона квадрата.

4. Радиус вписанной окружности для ромба:

r = h / 2,

где h — высота ромба.

5. Площадь четырёхугольника через радиус вписанной окружности:

S = r · p, где:

1. S — площадь четырёхугольника;
2. r — радиус вписанной окружности;
3. p — полупериметр (p = (a + b + c + d) / 2).

📌 Свойства вписанной окружности и n-угольника

1. Окружность можно вписать в правильный n-угольник, так как все его стороны равны, и суммы длин противоположных сторон также равны.

2. Центр вписанной окружности совпадает с центром правильного n-угольника, который является точкой пересечения биссектрис всех его углов.

3. Вписанная окружность касается каждой стороны правильного n-угольника в её середине.

📌 Формулы вписанной окружности и n-угольника

1. Сторона правильного n-угольника связана с радиусом вписанной окружности следующей формулой:

a = 2 · r · tg(180° / n), где:

1. a — длина стороны n-угольника;
2. r — радиус вписанной окружности;
3. n — количество сторон многоугольника.

2. Радиус вписанной окружности можно вычислить через площадь S и полупериметр p правильного n-угольника:

r = S / p, где:

1. p = (n · a) / 2 — полупериметр;
2. a — длина стороны n-угольника.

3. Для правильного n-угольника радиус вписанной окружности можно выразить через длину стороны a:

r = a / (2 · tg(180° / n)).

Частные случаи для правильных многоугольников:

— Для правильного треугольника (n = 3):

r = a / (2 · √3).

— Для правильного четырёхугольника (квадрата, n = 4):

r = a / 2.

— Для правильного шестиугольника (n = 6):

r = (a · √3) / 2.

4. Площадь правильного n-угольника можно вычислить по формуле:

S = n · r² · tg(180° / n), где:

1. S — площадь n-угольника;
2. r — радиус вписанной окружности;
3. n — количество сторон.

Описанная окружность

📎 Описанная окружность — это окружность, содержащая все вершины n-угольника, т. е. все вершины многоугольника лежат на окружности.

Вписанный многоугольник — это многоугольник, около которого описана окружность.

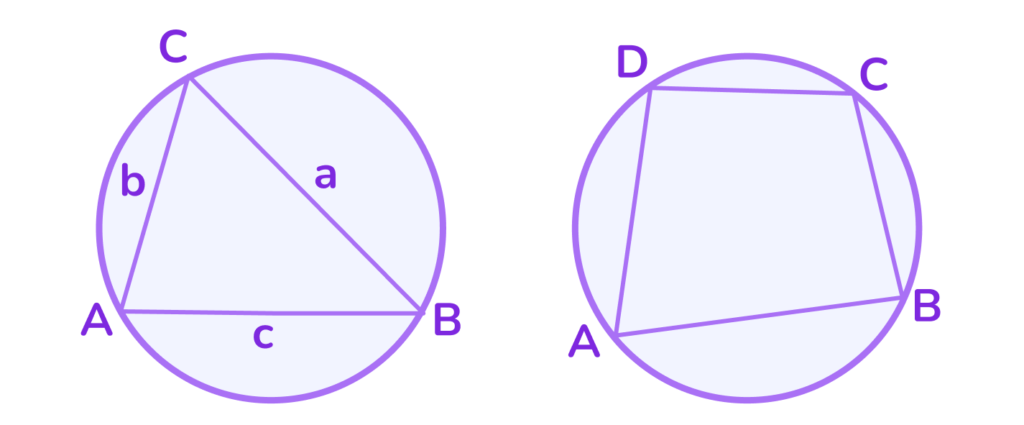
Окружность можно описать около ⤵︎

1. Треугольника: окружность можно описать около любого треугольника.

2. Четырёхугольника: окружность можно описать около четырёхугольника только в том случае, если сумма его противоположных углов равна 180°.

3. Правильного n-угольника: окружность можно описать около любого правильного многоугольника (все стороны и углы равны).

Свойства и формулы для описанной окружности 

📌 Свойства описанной окружности и треугольника

1. Окружность можно описать около любого треугольника , независимо от его типа (остроугольный, тупоугольный или прямоугольный).

2. Центр описанной окружности находится на пересечении серединных перпендикуляров к сторонам треугольника.

— Для остроугольного треугольника центр лежит внутри треугольника.

— Для тупоугольного треугольника центр лежит вне треугольника.

— А для прямоугольного треугольника центр совпадает с серединой гипотенузы.

3. Расстояние от центра описанной окружности до каждой вершины треугольника одинаково и равно радиусу окружности (R).

📌 Формулы описанной окружности и треугольника

1. Теорема синусов. Радиус описанной окружности связан со сторонами и углами треугольника через теорему синусов:

a / sin(A) = b / sin(B) = c / sin(C) = 2 · R, где:

1. a, b, c — стороны треугольника;
2. ∠A, ∠B, ∠C — противолежащие углы;
3. R — радиус описанной окружности.

2. Радиус описанной окружности можно вычислить через стороны и площадь треугольника:

R = (a · b · c) / (4 · S), где:

1. a, b, c — стороны треугольника;
2. S — площадь треугольника.

3. Для прямоугольного треугольника радиус описанной окружности равен половине гипотенузы:

R = c / 2

где c — гипотенуза.

📌 Свойства описанной окружности и четырёхугольника

1. Окружность можно описать около четырёхугольника только в том случае, если суммы его противоположных углов равны 180°:

∠A + ∠C = ∠B + ∠D = 180°.

2. Окружность можно описать около прямоугольника и квадрата, так как их противоположные углы равны 90° и их сумма составляет 180°.

3. Окружность можно описать около равнобедренной трапеции, так как её углы при основании равны, и сумма противоположных углов равна 180°.

4. Центр описанной окружности находится на пересечении серединных перпендикуляров к сторонам четырёхугольника.

5. Расстояние от центра описанной окружности до каждой вершины четырёхугольника одинаково и равно радиусу окружности (R).

📌 Формулы описанной окружности и четырёхугольника

1. Площадь четырёхугольника, около которого описана окружность, можно вычислить по формуле:

S = √((p-a) · (p-b) · (p-c) · (p-d)), где:

1. S — площадь четырёхугольника;
2. a, b, c, d — длины сторон;
3. p = (a + b +c + d) / 2 — полупериметр.

2. Частные случаи для правильных четырёхугольников:

— Для квадрата:
Радиус описанной окружности равен половине диагонали квадрата:

R = d / 2

где d — диагональ квадрата.

— Для прямоугольника:
Радиус описанной окружности также равен половине диагонали прямоугольника:

R = √(a² + b²) / 2

где a и b — стороны прямоугольника.

📌 Свойства описанной окружности и n-угольника

1. Окружность можно описать около правильного n-угольника, так как все его вершины лежат на окружности.

2. Центр описанной окружности совпадает с центром правильного n-угольника, который является точкой пересечения серединных перпендикуляров к его сторонам.

3. Расстояние от центра описанной окружности до каждой вершины n-угольника одинаково и равно радиусу окружности (R).

📌 Формулы описанной окружности и n-угольника

1. Сторона правильного n-угольника связана с радиусом описанной окружности следующей формулой:

a = 2 · R · sin(180° / n), где:

1. a — длина стороны n -угольника;
2. R — радиус описанной окружности;
3. n — количество сторон.

2. Для правильного n-угольника радиус описанной окружности можно выразить через длину стороны a:

R = a / (2 · sin(180° / n)).

3. Площадь правильного n-угольника можно вычислить по формуле:

S = (n · R² · sin(360° / n)) / 2, где:

1. S — площадь n-угольника;
2. R — радиус описанной окружности;
3. n — количество сторон.

4. Частные случаи для правильных многоугольников:

— Для правильного треугольника (n=3):

R = a / √3.

— Для квадрата (n=4):

R = a / √2.

— Для правильного шестиугольника (n=6):

R = a.

Вписанная и описанная окружность: памятка с формулами

Вписанная и описанная окружность — важные понятия геометрии, которые помогают устанавливать связь между многоугольниками и окружностями. Мы рассмотрели их основные свойства, условия существования и формулы для вычисления радиусов, площадей и других параметров.

Эти знания позволяют решать задачи на нахождение характеристик треугольников, четырёхугольников и правильных многоугольников, а также углубляют понимание взаимосвязи между различными геометрическими фигурами. Вписанная и описанная окружность.

Если возникают трудности с пониманием темы «Вписанная и описанная окружность», воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы.

Первый урок по форме ниже — бесплатный 💜