Теорема Фалеса

Теорема Фалеса — одна из фундаментальных теорем в геометрии, которая открывает путь к пониманию подобия фигур и пропорциональных соотношений. Эта теорема носит имя Фалеса Милетского, древнегреческого философа и математика, жившего в VI веке до нашей эры. Исторические свидетельства указывают, что Фалес использовал свои геометрические знания для решения практических задач — согласно легенде, он рассчитал высоту пирамиды Хеопса в Египте, измеряя длину её тени и сравнивая с тенью от палки известной высоты.

Значение теоремы Фалеса о пропорциональных отрезках выходит далеко за рамки школьного курса геометрии. Она находит применение в архитектуре, строительстве, навигации и даже искусстве. Например, в навигации существует правило: если суда движутся с постоянной скоростью и сохраняют курс друг на друга, то столкновение неизбежно — это прямое следствие теоремы Фалеса.

Изучение этой теоремы начинается в 8-м классе, и для учащихся её освоение создаёт основу для понимания последующих тем геометрии, особенно теории подобия треугольников. В статье мы подробно разберём саму теорему, её доказательство, специфику применения и решим несколько задач для закрепления материала.

Теорема Фалеса и её доказательство

Теорема Фалеса звучит так: если параллельные прямые пересекают две данные прямые и отсекают на одной из них равные отрезки, то они отсекают равные отрезки и на другой данной прямой.

Доказательство →

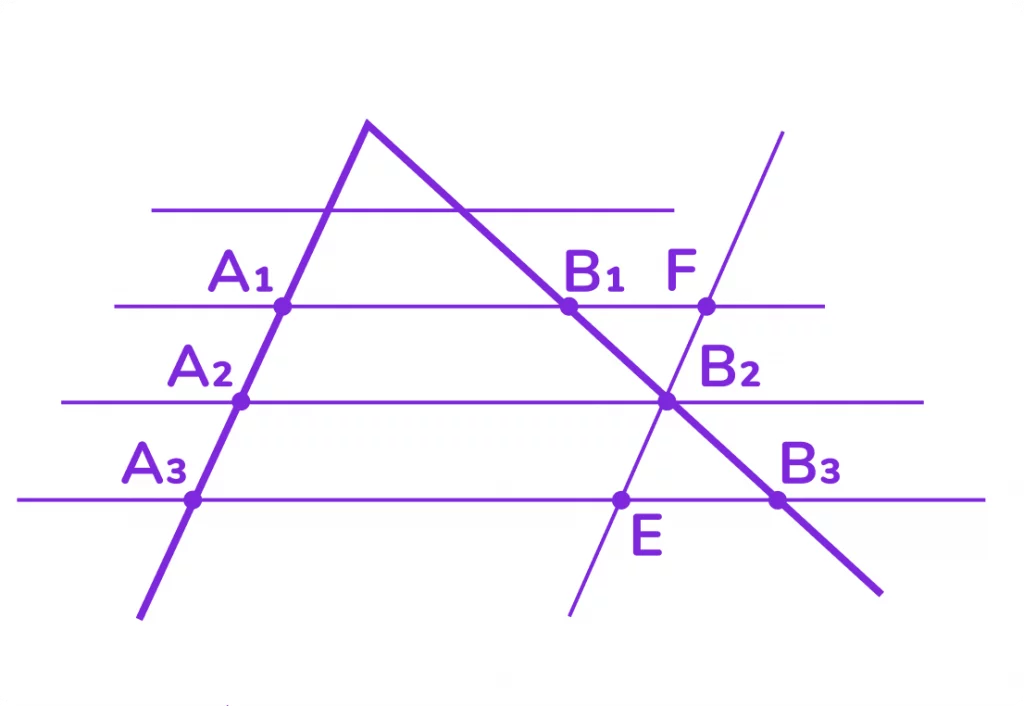
Пусть A₁, A₂, A₃ — точки пересечения параллельных прямых с одной из сторон угла и A₂ лежит между A₁ и A₃ (Рис. 1). Пусть B₁, B₂, B₃ — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A₁A₂ = A₂A₃, то B₁B₂ = B₂B₃.

Проведём через точку B₂ прямую EF, параллельную прямой A₁A₃. По свойству параллелограмма A₁A₂ = FB₂, A₂A₃ = B₂E. И так как A₁A₂ = A₂A₃, то FB₂ = B₂E.

Треугольники B₂BF и B₂B₃E равны по второму признаку равенства треугольников (у них B₂F = B₂E по доказанному; углы при вершине B₂ равны, как вертикальные, а углы B₂FB₁ и B₂EB₃ равны как внутренние накрест лежащие при параллельных A₁B₁ и A₃B₃ и секущей EF).

Из равенства треугольников следует равенство сторон: B₁ B₂ =B₂ B₃ . 

Теорема доказана.

Замечание об обратном утверждении

Важно понимать, что обратное утверждение не всегда является верным.

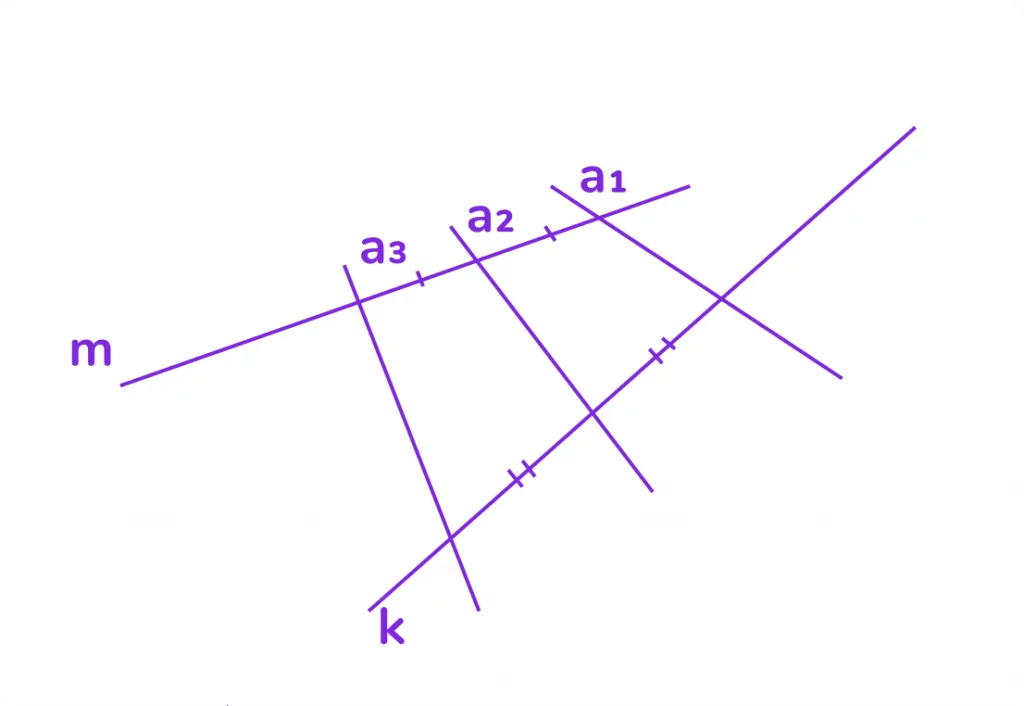
Нельзя в общем случае утверждать, что если некоторые прямые пересекают две данные прямые и отсекают на каждой из них равные отрезки, то исходные прямые между собой параллельны. На рисунке 2 можно увидеть, что прямые отсекают равные отрезки, но параллельными не являются.

Пример решения задачи

Задача 1. Разделите данный отрезок AB на n равных частей.

Решение: 

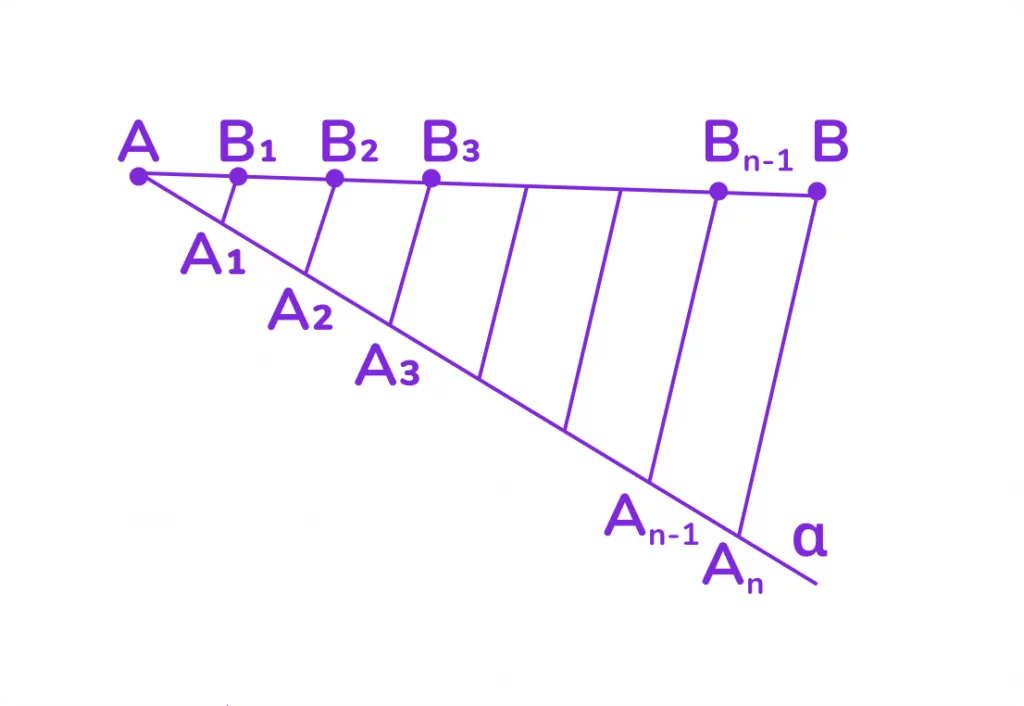
Проведём из точки A полупрямую a, не лежащую на прямой AB. Отложим на полупрямой a равные отрезки: AA₁, A₁A₂, A₂A₃, …, A_n-1A_n. (Рис. 3).

Соединим точки A_n и B. Проведём через точки A₁, A₂, … , A_n-1 прямые, параллельные прямой A_nB. Они пересекают отрезок AB в точках B₁, B₂, …, B_n-1, которые
делят отрезок AB на n равных отрезков (по теореме Фалеса).

📝 Задание для самопроверки

А теперь попробуйте решить задание по этой теме самостоятельно!

Задание 1. 

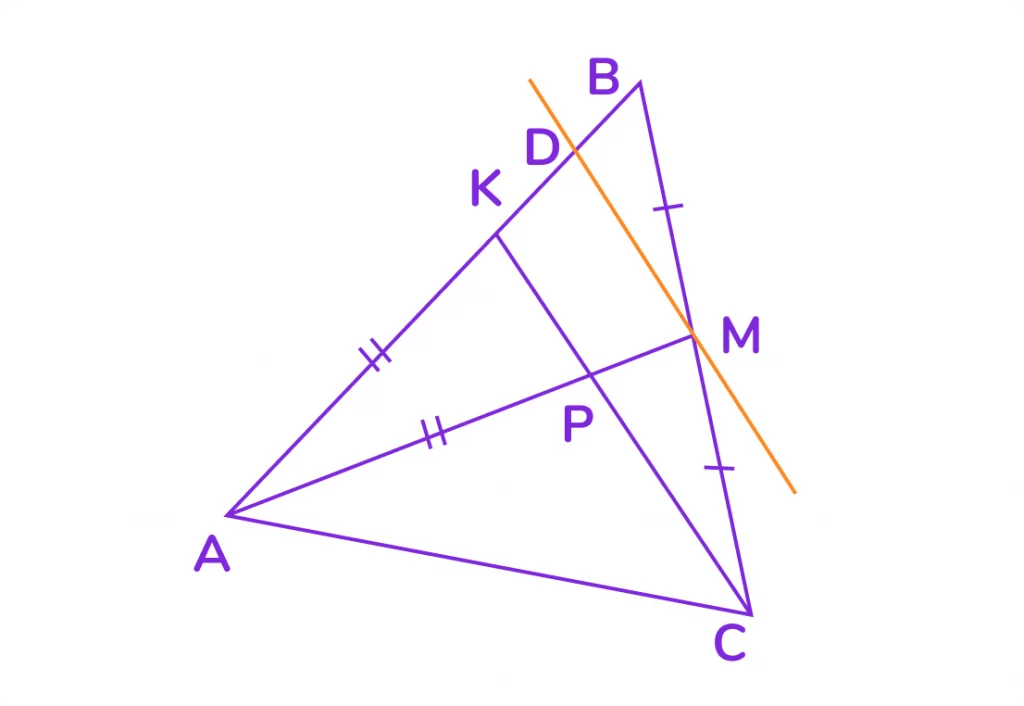
На стороне AB треугольника ABC отмечена точка K. Отрезок CK пересекает медиану AM треугольника в точке P. Оказалось, что AK = AP. Найдите отношение BK : PM .

Решение:

1. Проведём через точку M прямую, параллельную CK, которая пересечёт AB в точке D.

2. По теореме Фалеса: BD = KD (так как BM = MC, DM || KC).

3. Рассмотрим подобные треугольники APK и AMD (подобны по двум углам). Так как AK = AP, то треугольник APK равнобедренный, значит, и треугольник AMD — равнобедренный (AD = AM). Следовательно, KD = PM.

4. Таким образом, BK : PM = 2 : 1

Ответ: BK : PM = 2 : 1

Подведём итоги

Теорема Фалеса изучается в курсе геометрии 8-го класса и является мощным инструментом для решения разнообразных задач. Её роль в математике трудно переоценить ⤵

1. Историческое значение. Теорема одна из первых установила строгие количественные соотношения в геометрии.

2. Образовательное значение. Она формирует мост между элементарной геометрией и теорией подобия, открывая путь к более сложным разделам математики.

3. Практическое применение. От архитектуры и строительства до навигации и дизайна — теорема Фалеса находит многочисленные применения в реальной жизни.

4. Развитие логического мышления. Доказательство теоремы и решение связанных с ней задач развивает логическое и пространственное мышление.

Как заметил один из современных педагогов: «Понимание теоремы Фалеса — это ключ к пониманию подобия, а понимание подобия — это ключ к пониманию геометрии в целом». Освоение этой теоремы откроет перед учащимися новые возможности для решения сложных геометрических проблем.