Таблицы истинности

Таблицы истинности — это математический инструмент для анализа логических выражений. Они позволяют определить значение сложного высказывания при всех возможных комбинациях исходных данных.

🕰️ Историческая справка: основы логики заложил Джордж Буль (1815–1864) в работе «Исследование законов мысли». Его труды положили начало булевой алгебре — фундаменту цифровых технологий.

Значение таблиц истинности в современном мире сложно переоценить. Они широко  используются в проектировании процессоров, написании программ, создании искусственного интеллекта и баз данных.

Основные понятия и логические операции

Логическое высказывание — утверждение, которое может быть истинным (1) или ложным (0).

Например, про следующие утверждения мы можем точно сказать истинны они или нет. Так утверждение «2 + 2 = 4» — истинно, значит это логическое высказывание. Выражение «Земля плоская» — ложно, значит это утверждение также является логическим высказыванием.

Логические переменные — символы, обозначающие высказывания (A, B, C).

Простые высказывания содержат одну мысль, составные объединяют несколько простых через логические операции.

1️⃣ Базовые логические операции

Логическое И (конъюнкция)

Это базовая логическая операция, которая возвращает значение «истина» только тогда, когда оба исходных высказывания истинны. Во всех остальных случаях результат будет «ложь».

Обозначения: ∧, AND, &

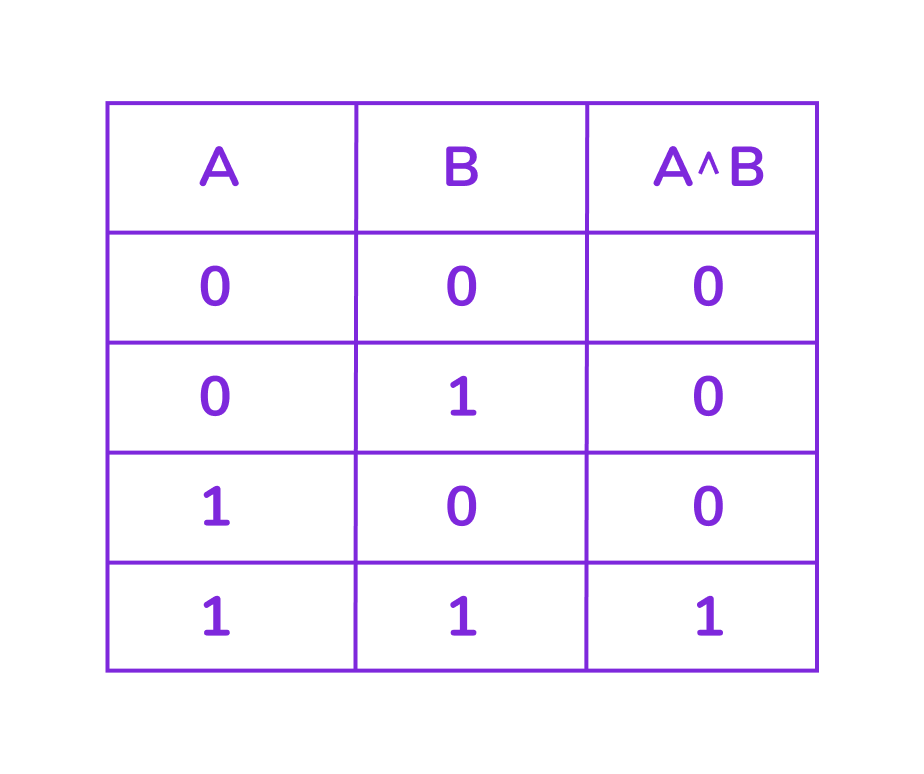
Пример: «Идёт дождь И я дома» — истинно только при одновременном выполнении условий.

Логическое ИЛИ (дизъюнкция)

Это логическая операция, которая возвращает значение «истина», когда хотя бы одно из исходных высказываний истинно. Результат будет «ложь», только если все высказывания ложны.

Обозначения: ∨, OR, |

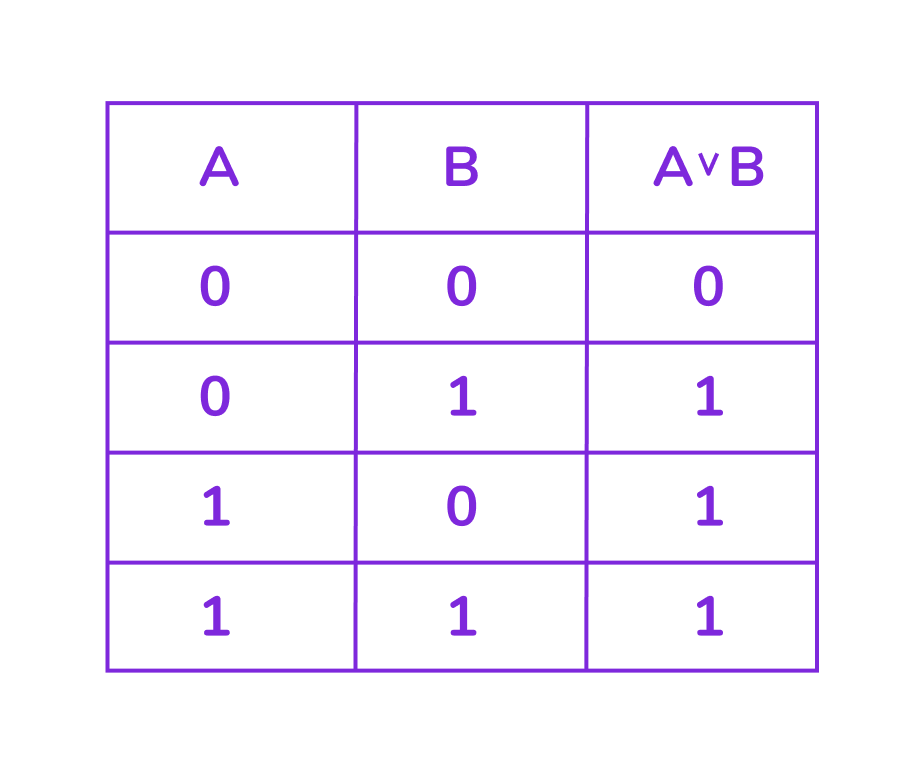
Пример: «Я пойду в кино ИЛИ в театр» — истинно при выполнении хотя бы одного условия.

Логическое НЕ (отрицание)

Это логическая операция, которая инвертирует значение высказывания. Если исходное высказывание истинно, отрицание делает его ложным, и наоборот.

Обозначения: ¬, NOT, !

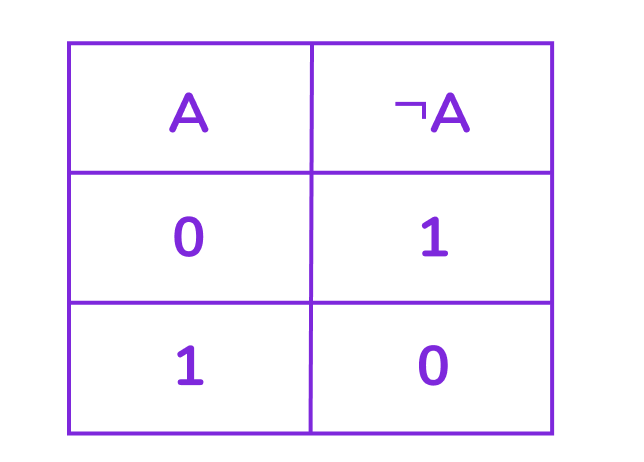
Пример: «НЕ сегодня понедельник» — истинно во все дни, кроме понедельника.

2️⃣ Дополнительные операции

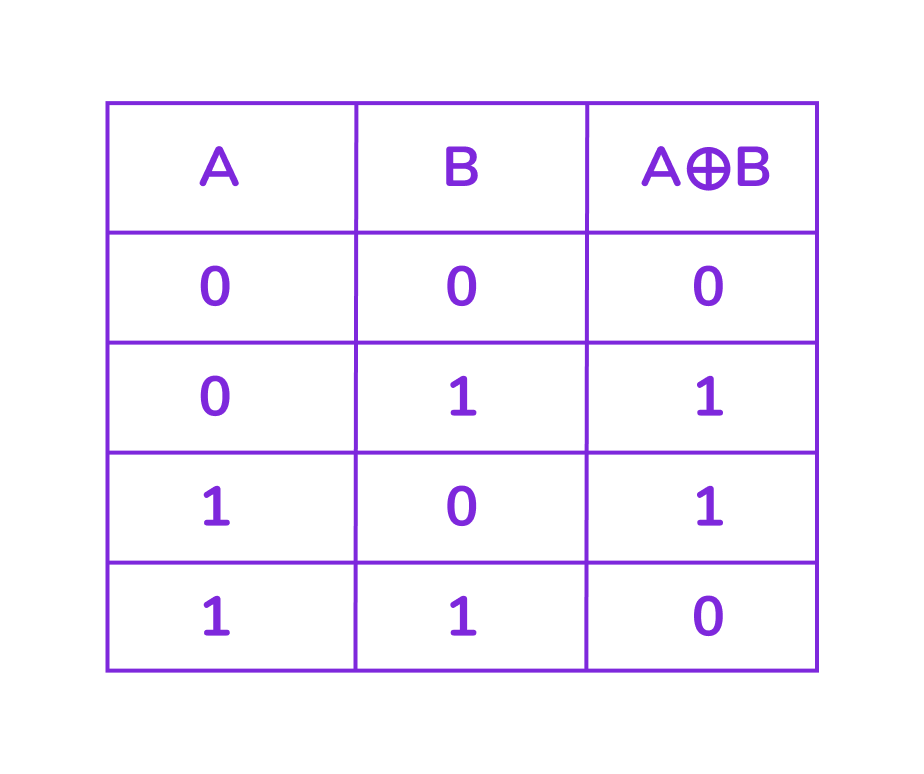
Исключающее ИЛИ (XOR)

Это логическая операция, которая возвращает значение «истина», только когда исходные высказывания имеют разные значения. Если высказывания одинаковы (оба истинны или оба ложны), результат будет «ложь».

Обозначение: ⊕

Импликация: «Если A, то B»

Импликация ложна (0) только в одном случае: когда условие A истинно, а следствие B ложно. Во всех остальных случаях импликация истинна (1).

Обозначение:  →

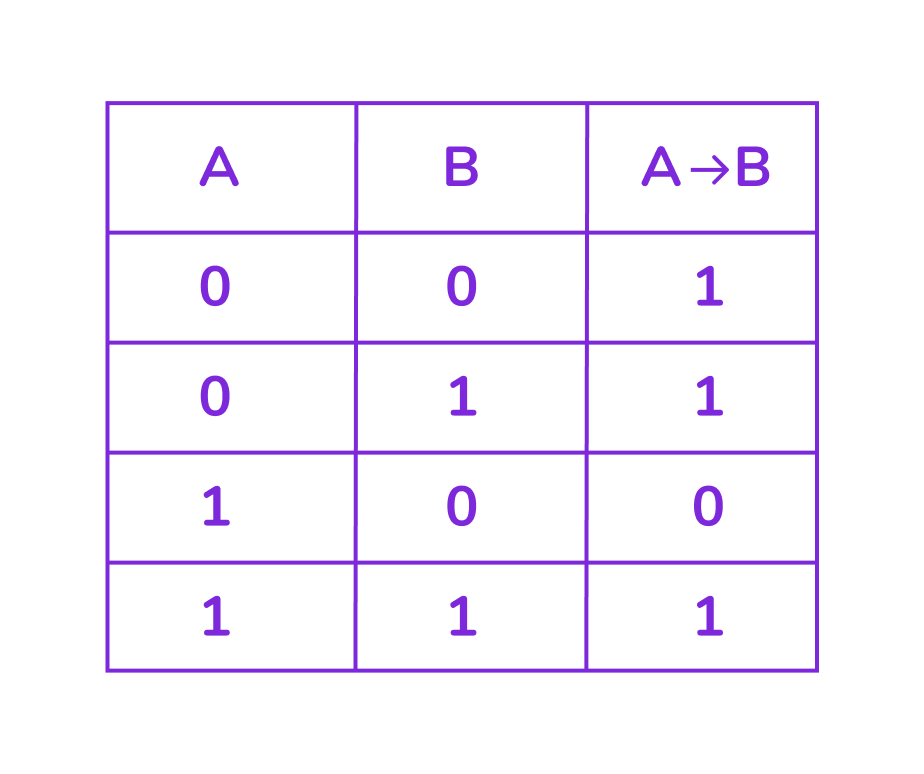
Рассмотрим примеры для понимания этой операции:

1. «Если идёт дождь (A=1), то я беру зонт (B=1)» → истинно (1).
2. «Если идёт дождь (A=1), то я беру зонт (B=0)» → ложно (0) — нарушение обещания.
3. Или «Если не идёт дождь (A=0), то я беру зонт (B=1)» → истинно (1) — я могу взять зонт для защиты от солнца.
4. «Если не идёт дождь (A=0), то я беру зонт (B=0)» → истинно (1) — логичное поведение.

Эквивалентность: «A тoгда и только тогда, когда B».

Эквивалентность истинна (1), только когда A и B равны (оба 0 или оба 1). И эквивалентность ложна (0), когда A и B разные (0 и 1, или 1 и 0).

Обозначение: ↔

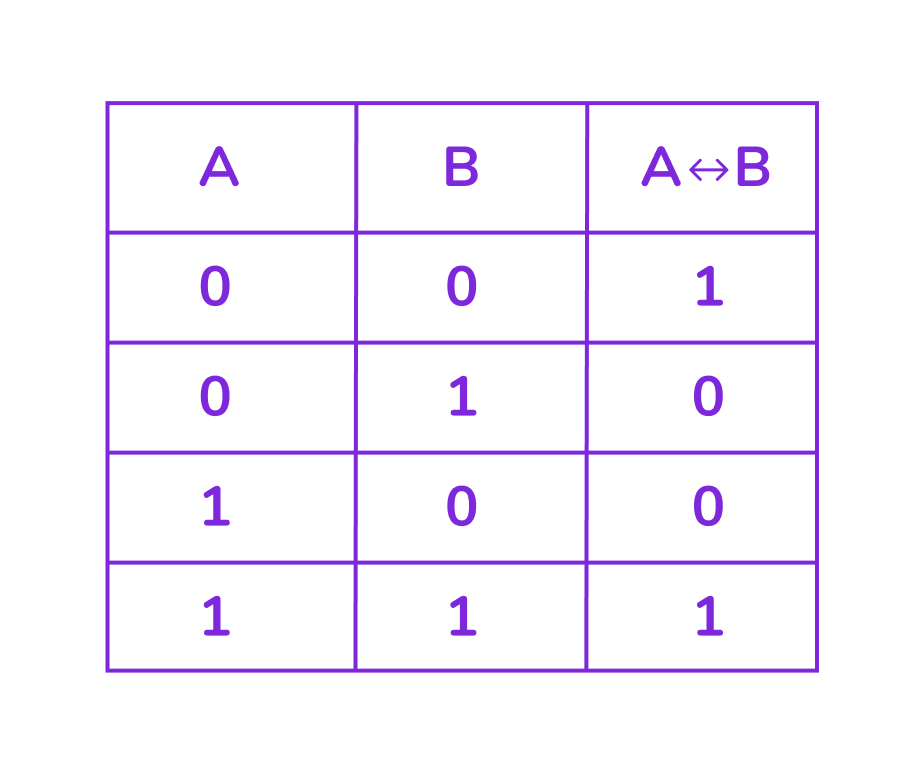
Примеры для понимания операции эквивалентность:

1. «Я пойду гулять (A=1) тогда и только тогда, когда сделаю уроки (B=1)» → истинно (1).
2. «Я пойду гулять (A=1) тогда и только тогда, когда не сделаю уроки (B=0)» → ложно (0).
3. Или «Я не пойду гулять (A=0) тогда и только тогда, когда не сделаю уроки (B=0)» → истинно (1).
4. «Я не пойду гулять (A=0) тогда и только тогда, когда сделаю уроки (B=1)» → ложно (0).

Приоритет логических операций

Логические операции важно выполнять в правильном порядке:

1. Скобки.

2. НЕ (¬).

3. И (∧).

4. ИЛИ (∨).

5. Импликация (→).

6. Эквивалентность (↔).

Построение таблиц истинности

При построении таблиц истинности важно придерживаться определённого алгоритма. Познакомимся с ним и рассмотрим его применение на примерах. 

Алгоритм построения таблицы истинности:

1️⃣ Определить количество переменных (n).

2️⃣ Вычислить количество строк: 2ⁿ.

3️⃣ Заполнить столбцы входных переменных.

4️⃣ Добавить столбцы промежуточных операций.

5️⃣ Заполнить столбец итогового выражения.

Рассмотрим пример для двух переменных. 

Пример 1. Построить таблицу истинности для выражения:  A ∧ B ∨ ¬A.

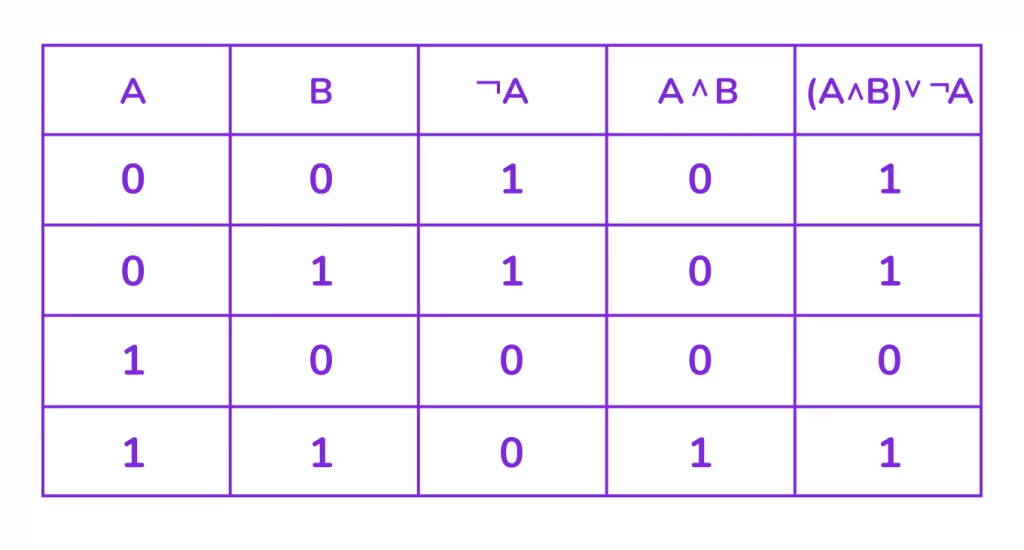
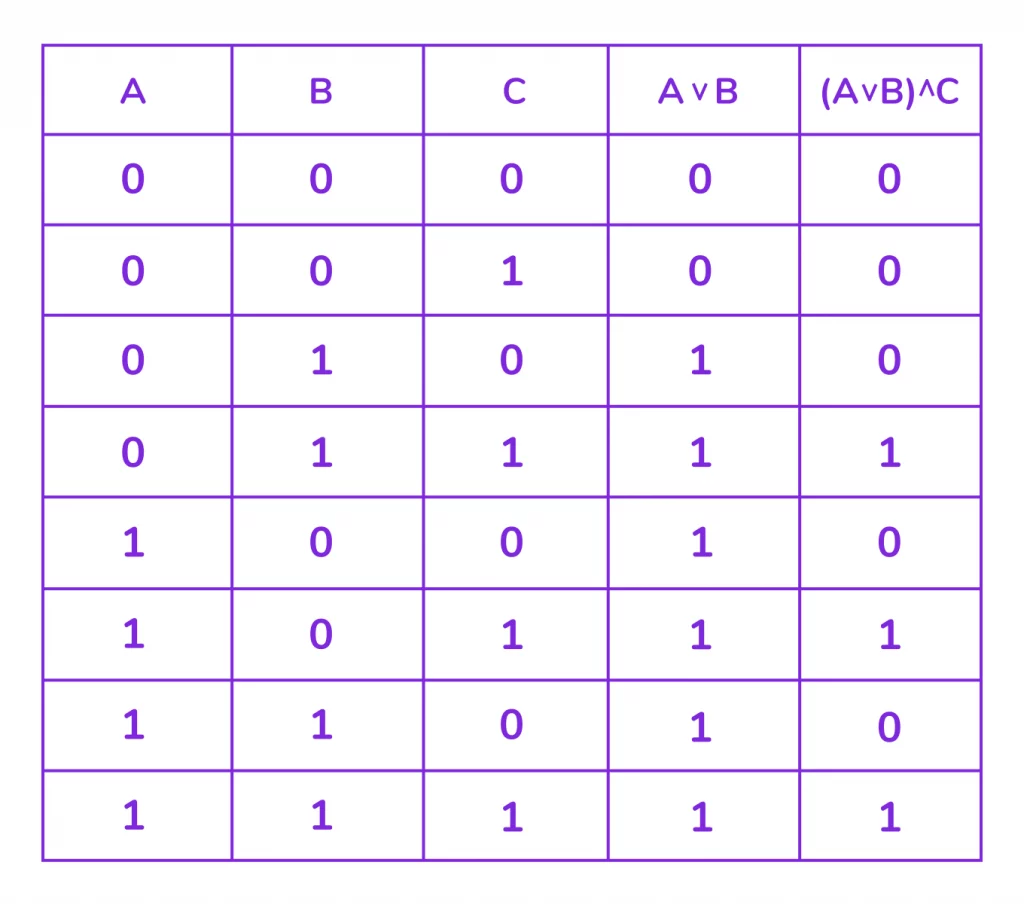
Теперь рассмотрим пример построения таблицы истинности для выражения с тремя переменными. 

Пример 2. Построить таблицу истинности для выражения:  (A ∨ B) ∧ C.

📝 Упражнение для самопроверки

Упражнение. Постройте таблицу истинности для: ¬(A ∨ B).

Решение ⤵

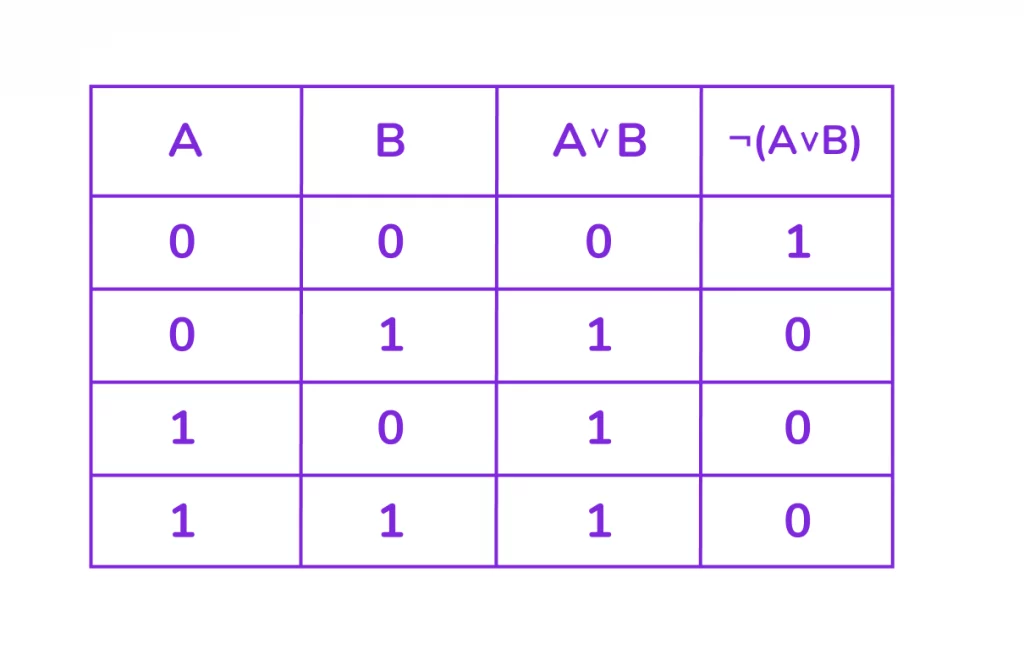
1. A ∨ B (ИЛИ) — ложно (0), только когда оба операнда ложны (0), во всех остальных случаях истинно (1).

2. ¬(A ∨ B) (НЕ) — инвертирует результат операции A ∨ B.

3. Выражение ¬(A ∨ B) истинно, только когда оба исходных высказывания A и B ложны.

Подведём итоги

Мы изучили таблицы истинности и узнали, что таблицы истинности — мощный инструмент анализа логических выражений; они основаны на строгих математических принципах; знание логических операций необходимо для программирования.

Таблицы истинности широко применяются в следующих сферах:

1. Проектирование цифровых схем.
2. Написание условий в программах.
3. Создание баз данных.
4. Разработка алгоритмов ИИ.

Полученные знания станут основой для изучения архитектуры, компьютеров, языков программирования и теории алгоритмов.