
Сумма и разность кубов
Сегодня мы разберём очень важную и полезную тему — «Сумма и разность кубов». Их изучение начинается в 7-м классе, а применение продолжается на протяжении всего курса школьной алгебры. Эти формулы помогут вам быстро и легко раскладывать сложные выражения на множители, что часто встречается в учебниках по алгебре и на контрольных работах.
После разложения многочлена на множители проще работать с выражениями, решать уравнения и упрощать задачи. В статье мы последовательно изучим формулы, рассмотрим, как они выводятся, и решим практические задания для закрепления материала.
Рассмотрим две формулы — важно понимать, как они устроены и почему работают:
- сумма кубов: выражение вида a3 + b3;
- разность кубов: выражение вида a3 − b3.

Формула суммы кубов
Рассмотрим выражение a3 + b3, разложив его на множители.
Для начала вспомним формулу для разложения разности квадратов:
x2 − y2 = (x − y)(x + y).
Сумма кубов тоже раскладывается на два множителя:
a3 + b3 = (а + b)( ? )
Теперь разберёмся, что находится в скобках вместо «?».
Если выполнить умножение двух многочленов (a + b)(a2 − аb + b2), то получится:
(а + b)(a2 − ab + b2) =
= a⋅a2 − a⋅ab + a⋅b2 + b⋅a2 − b⋅ab + b⋅b2 = a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3
Обратите внимание, что −a2b + a2b = 0 и ab2 − ab2 = 0, эти слагаемые взаимно уничтожаются.
Поэтому формула суммы кубов имеет вид:
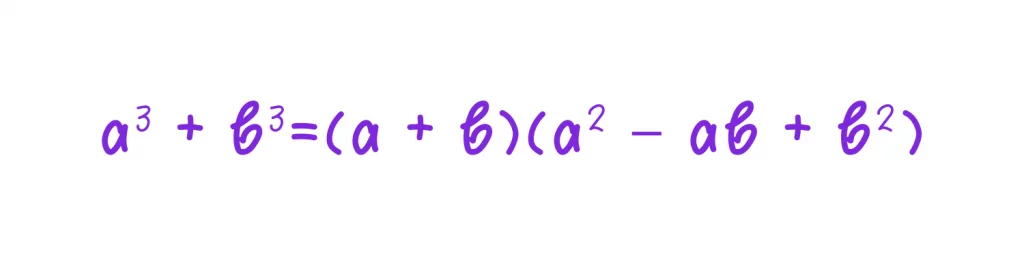
👉 Обратите внимание, что во второй скобке здесь минус и плюс, а в первой только плюс.
Задание на применение формулы суммы кубов
Посмотрим, как применяется изученная формула при решении заданий.
Задание 1. Разложить на множители выражение 64x3+27.
Решение:
- Представляем каждое слагаемое в виде куба: 64×3 = (4x)3, 27 = 33.
- Применяем формулу суммы кубов: a3 + b3 = (a + b)(a2 — ab + b2). В нашем случае: a = 4x, b = 3.
- Подставляем в формулу и упрощаем: 64×3 + 27 = (4x)3 + 33 = (4x + 3)((4x)2 — (4x)(3) + 32) = (4x + 3)(16×2 — 12x + 9).
Ответ: (4x + 3)(16x2 — 12x + 9).
Формула разности кубов
Теперь рассмотрим выражение a3 — b3.
Аналогично предыдущему разложим его на множители вида:
a3 — b3=(a — b)( ? )
Найдём «?» путём умножения двух многочленов и сравнения результата с левой частью:
(a − b)(a2 + ab + b2) = a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3.
На этот раз +a2 b−a2 b=0 и +ab2−ab2=0 взаимно уничтожаются. Таким образом получаем формулу разности кубов:
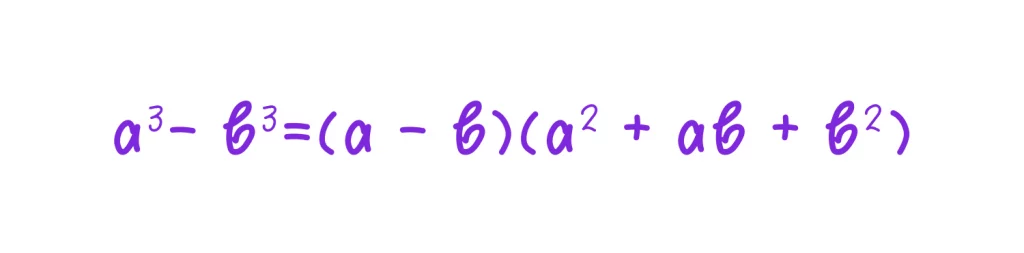
👉 Обратите внимание, что во второй скобке здесь плюсы, а в первой минус.
Задание на применение формулы разности кубов
Теперь научимся применять полученную формулу при решении заданий.
Задание 2. Разложить на множители выражение 27x3 − 8.
Решение:
- Представляем каждое слагаемое в виде куба: 27×3 = (3x)3, 8 = 23.
- Применяем формулу разности кубов: a3 — b3 = (a — b)(a2 + ab + b2). В нашем случае: a = 3x, b = 2.
- Подставляем в формулу и упрощаем: 27×3 − 8 = (3x)3 − 23 = (3x − 2)((3x)2 + (3x)(2) + 22) = (3x − 2)(9×2 + 6x + 4).
Ответ: (3x − 2)(9x2 + 6x + 4)
📝 Сумма и разность кубов: упражнение для самопроверки
А теперь попробуйте самостоятельно решить упражнение по этой теме.
Задание. Разложить на множители:
- x3 + 125;
- 64 − y3.
Решение:
1. Применяем формулу суммы кубов: a3 + b3 = (a + b)(a2 − ab + b2), где a = x, b = 5:
х3 + 53 = (x + 5)(x2 − x⋅5 + 52) = (x + 5)(x2 − 5x + 25).
2. Применяем формулу разности кубов: a3 − b3 = (a − b)(a2 + ab + b2), где a = 4, b = y:
43 − y3 = (4 − y)(42 + 4⋅y + y2) = (4 − y)(16 + 4y + y2).
Ответ:
1. (x + 5)(x2 − 5x + 25);
2. (4 − y)(16 + 4y + y2).
Подведём итоги по теме «Сумма и разность кубов»
Мы изучили две важные формулы алгебры:
- Сумма кубов: a3 + b3 = (a + b)(a2 − ab + b2),
- Разность кубов: a3 − b3 = (a − b)(a2 + ab + b2).
Они помогают быстро раскладывать выражения на множители, делают тождественные преобразования и решения уравнений более простыми.
Помните: чтобы успешно ими пользоваться, надо много практиковаться!
Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы. Первый урок — бесплатный 💜
 2
2
 3
3
 1
1








Комментарии 0