Как найти среднюю линию треугольника

Средняя линия треугольника — это важное понятие, которое изучается в 8-м классе на уроках геометрии. Она помогает лучше понять свойства треугольников и решать задачи, связанные с их сторонами и площадью. В этой статье мы разберём, что такое средняя линия треугольника, как её найти и какие у неё свойства, узнаем, как использовать теорему о средней линии для решения задач, а также научимся применять эти знания на практике.

Треугольник: понятие, виды, свойства

📎 Треугольник — это одна из самых простых и важных геометрических фигур. Он состоит из трёх точек, которые не лежат на одной прямой, и трёх отрезков, соединяющих эти точки.

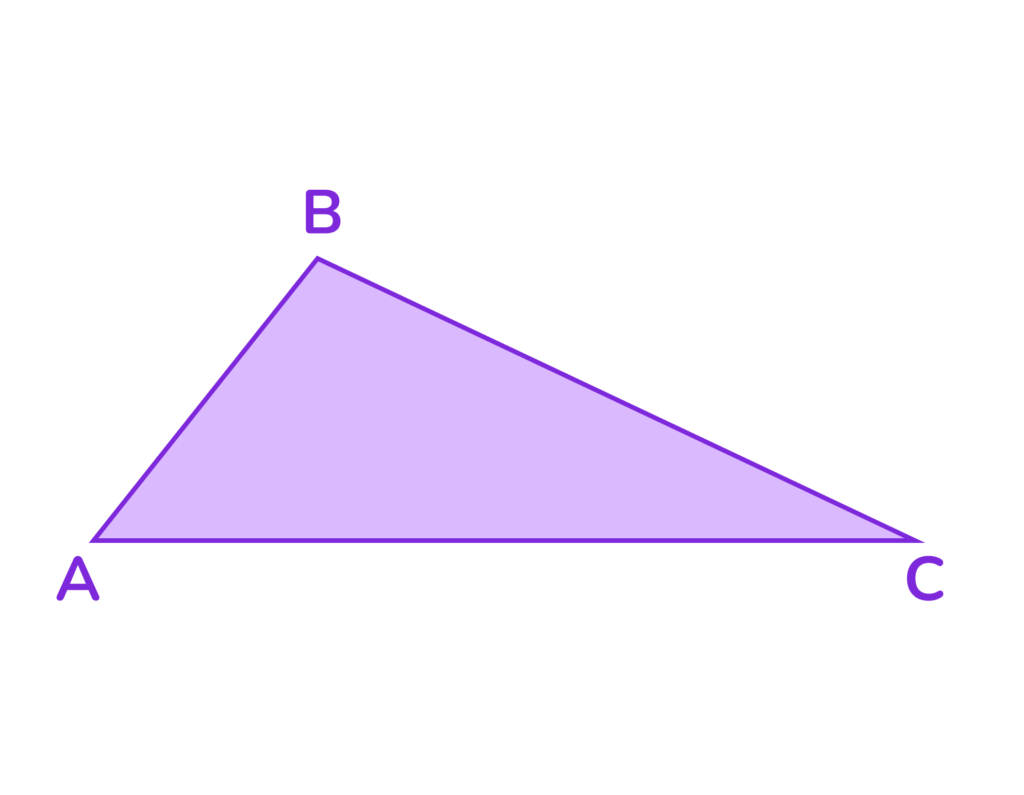
Основные элементы треугольника:

1. Вершины — три точки, которые образуют треугольник (обычно обозначаются буквами A, B, C).
2. Стороны — три отрезка, соединяющие вершины (AB, BC, AC).
3. Углы — три угла, образованные парами сторон при каждой вершине (∠A, ∠B, ∠C).

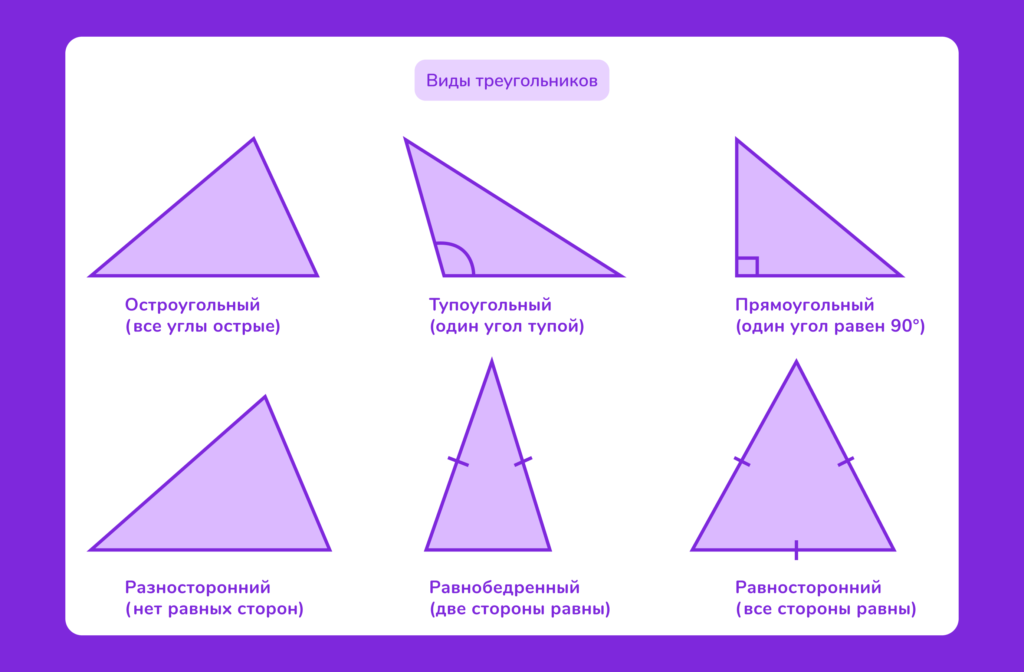
Треугольники классифицируются по сторонам и углам:

— По сторонам:

1. Разносторонний треугольник — все стороны имеют разную длину.
2. Pавнобедренный треугольник — две стороны равны.
3. Равносторонний треугольник — все три стороны равны. Равносторонний треугольник также называют правильным треугольником. У него все углы равны 60°.

— По углам:

1. Остроугольный треугольник — все углы меньше 90°.
2. Прямоугольный треугольник — один из углов равен 90°. В прямоугольном треугольнике сторона, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны — катетами.
3. Тупоугольный треугольник — один из углов больше 90°.

Свойства треугольника:

1. Сумма всех углов треугольника всегда равна 180°.
2. В треугольнике против большей стороны лежит больший угол, и наоборот.
3. Любой треугольник можно вписать в окружность (описанная окружность) и описать вокруг окружности (вписанная окружность).

Понятие средней линии треугольника

📎 Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. Она обладает важными свойствами и играет ключевую роль в геометрии треугольников.

Определение. Если в треугольнике ABC отметить середины сторон AB и BC (обозначим их как M и N соответственно), то отрезок MN называется средней линией треугольника.

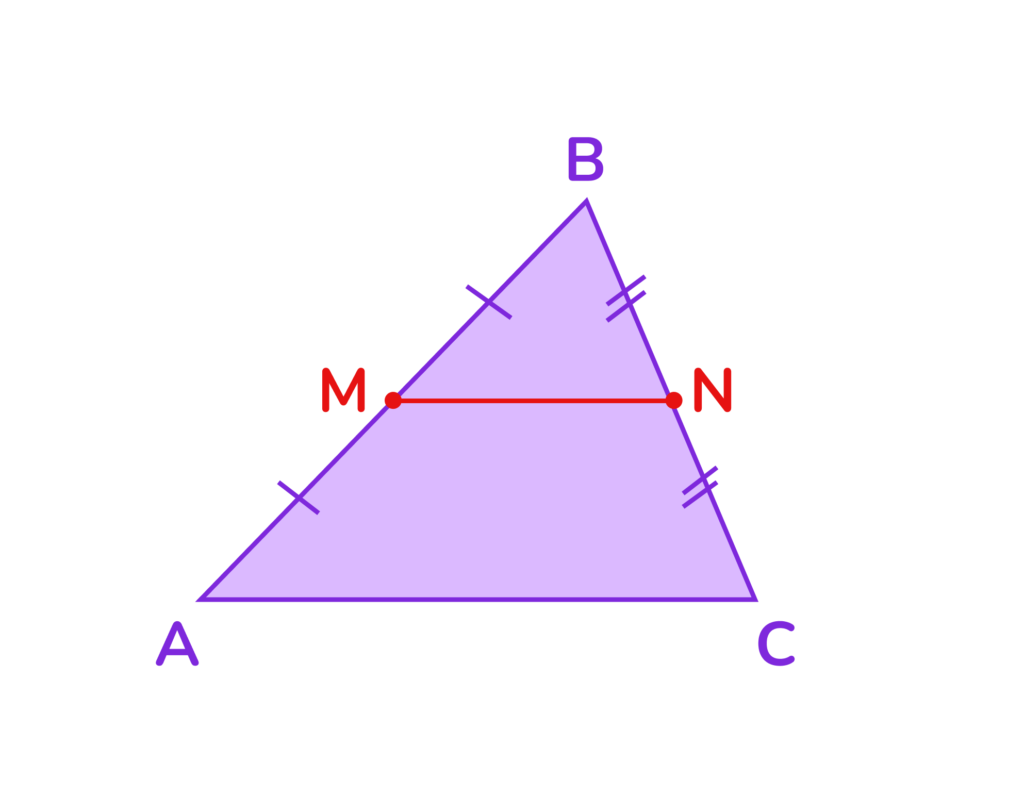
Пусть в треугольнике ABC:

1. Точка N — середина стороны BC.

Тогда отрезок MN является средней линией треугольника ABC.

Cредняя линия помогает делить треугольник на две части:

1. Меньший треугольник, подобный исходному.
2. Трапецию, образованную средней линией и одной из сторон треугольника.

Средняя линия прямоугольного треугольника

📎 Cредняя линия прямоугольного треугольника — это отрезок, который соединяет середины двух его сторон. Она обладает теми же свойствами, что и средняя линия любого другого треугольника, но имеет особенности из-за наличия прямого угла.

Определение. Если в прямоугольном треугольнике ABC с прямым углом C отметить середины катетов AC и BC (точки M и N), то отрезок MN называется средней линией прямоугольного треугольника.

Cвойства средней линии треугольника

Средняя линия треугольника обладает важными свойствами, которые помогают решать геометрические задачи. Рассмотрим их подробнее ⤵

1. Параллельность стороне треугольника
Средняя линия всегда параллельна одной из сторон треугольника. Например, если в треугольнике △ABC провести среднюю линию MN, соединяющую середины сторон AB и AC, то она будет параллельна стороне BC.

2. Длина средней линии
Длина средней линии равна половине длины той стороны, которой она параллельна. Например:

MN = ½ BC.

3. Деление треугольника на подобные части
Средняя линия отсекает треугольник, который подобен исходному треугольнику с коэффициентом подобия ½. Площадь отсечённого треугольника составляет одну четверть площади исходного треугольника.

4. Разделение треугольника на четыре равных треугольника
Три средние линии разделяют исходный треугольник на четыре равных треугольника. Центральный из них называют дополнительным треугольником.

5. Особенность прямоугольного треугольника
В прямоугольном треугольнике три средние линии разделяют его на четыре равных прямоугольных треугольника.

Теорема о средней линии треугольника

Теорема:
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Формулировка:

Если в треугольнике △ABC провести среднюю линию MN, соединяющую середины сторон AB и AC, то:

1. MN ∥ BC (средняя линия параллельна третьей стороне).
2. MN = ½ BC (длина средней линии равна половине длины третьей стороны).

Доказательство:

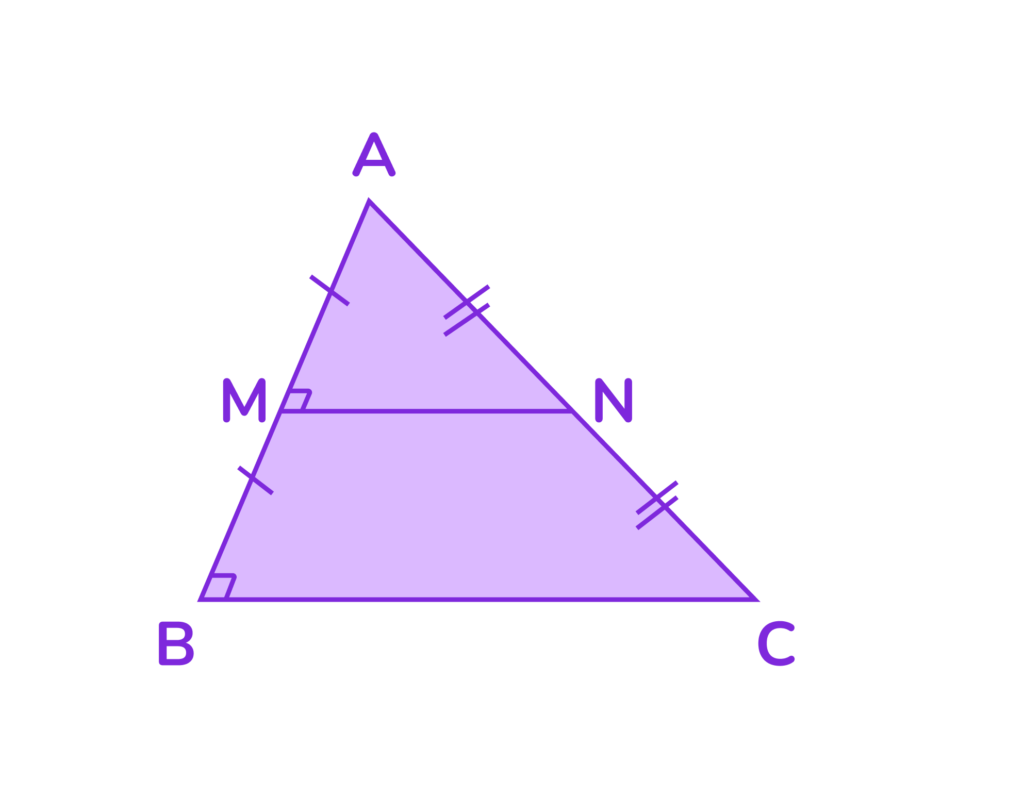
1. По условию, точки M и N — середины сторон AB и AC. Это означает:

1. AM = MB;
2. AN = NC.

2. Рассмотрим треугольники △AMN и △ABC:

1. Угол ∠A у них общий.
2. Стороны AM и AN равны половинам сторон AB и AC соответственно.

3. Из этого следует, что треугольники △AMN и △ABC подобны по второму признаку подобия (два угла одного треугольника равны двум углам другого, а соответствующие стороны пропорциональны).

4. Коэффициент подобия равен ½, так как AM = ½ AB и AN = ½ AC.

5. Из подобия треугольников следует:

1. MN ∥ BC (соответственные углы равны, значит, прямые параллельны).
2. MN = ½ BC (соотношение длин сторон определяется коэффициентом подобия).

Теорема доказана.

Средняя линия треугольника: решение задач по теме

👉 Пример 1

Условие:
В треугольнике △ABC сторона BC = 18. Проведена средняя линия MN, параллельная стороне BC. Найдите длину MN.

Решение:
По теореме о средней линии треугольника:

MN = ½ BC.

Подставляем значение BC = 18:

MN = ½ ⋅ 18 = 9.

Ответ: длина средней линии MN = 9.

👉 Пример 2

Условие:
В треугольнике △ABC стороны равны: AB = 8, BC = 7, AC = 5. Точки M, N, K — середины сторон AB, BC, AC соответственно. Найдите периметр треугольника △MNK, образованного средними линиями.

Решение:
Средние линии треугольника равны половинам соответствующих сторон:

MN = ½ AC = ½ ⋅ 5 = 2,5. 

NK = ½ AB = ½ ⋅ 8 = 4. 

MK = ½ BC = ½ ⋅ 7 = 3,5.

Периметр треугольника △MNK:

P = MN + NK + MK = 2,5 + 4 + 3,5 = 10.

Ответ: периметр треугольника △MNK = 10.

👉 Пример 3

Условие:
В прямоугольном треугольнике △ABC проведены две средние линии: MN = 3 (параллельна катету AC) и NP = 4 (параллельна катету BC). Найдите площадь треугольника △ABC.

Решение:
По теореме о средней линии:

AC = 2 ⋅ MN = 2 ⋅ 3 = 6. 

BC = 2 ⋅ NP = 2 ⋅ 4 = 8.

Площадь прямоугольного треугольника:

S = ½ ⋅ AC ⋅ BC = ½ ⋅ 6 ⋅ 8 = 24.

Ответ: площадь треугольника △ABC = 24.

Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы. Заполняйте форму ниже, чтобы записаться на бесплатный вводный урок ⤵