Средняя линия трапеции

Сегодня мы изучим одну из важнейших тем в геометрии — средняя линия трапеции и её свойство. Трапеция — это фигура, которая часто встречается в архитектуре, строительстве и технике, поэтому понимание её свойств имеет практическое значение. Разбор этой темы не только поможет успешно справляться с геометрическими задачами, но и разовьёт пространственное мышление и логику.

Определение средней линии трапеции

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.

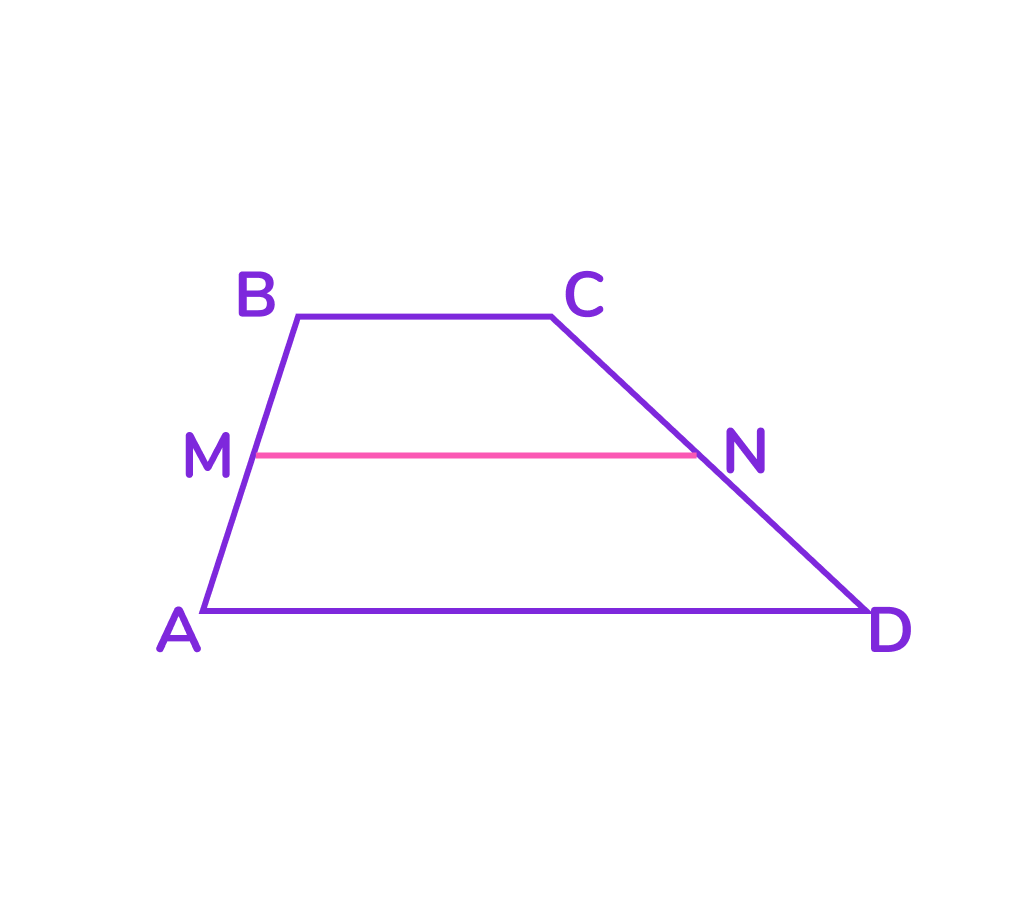
Рассмотрим трапецию ABCD с основаниями AD и BC (AD ∥ BC).

Пусть: точка M — середина боковой стороны AB; точка N — середина боковой стороны CD.

Тогда отрезок MN — средняя линия трапеции ABCD.

Свойство средней линии трапеции

Теорема: средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство →

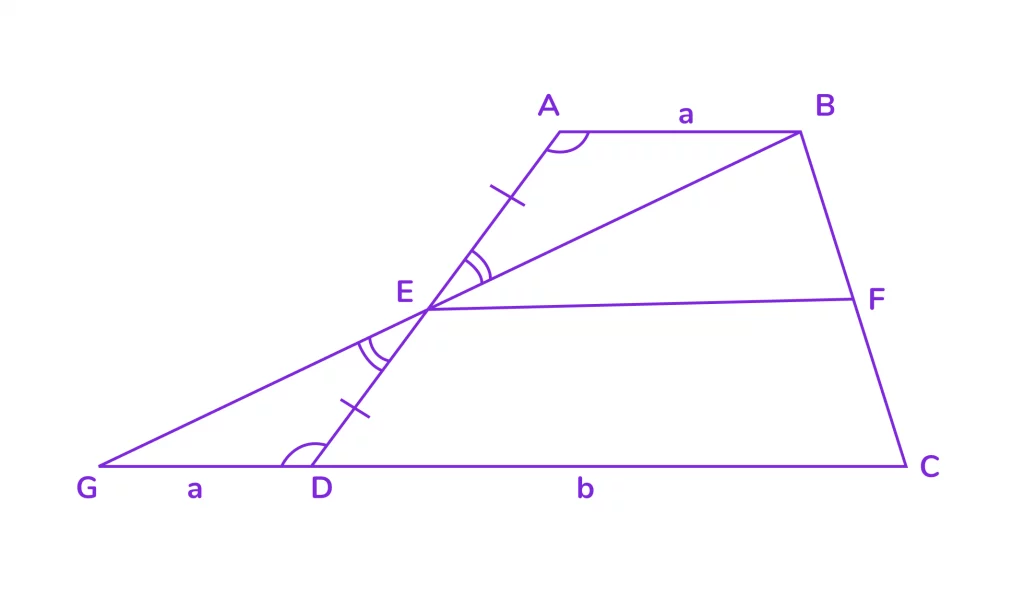
Трапеция ABCD,  её средняя линия — отрезок EF. Надо доказать, что отрезок EF параллелен основаниям трапеции CD и AB и равен половине суммы этих оснований, то есть (a + b) / 2. 

Вершину трапеции — точку B — соединим с концом средней линии — точкой E — и продолжим получившийся отрезок до пересечения с продолжением основания CD в точке G. Получились два треугольника GDE и BAE. 

В этих треугольниках углы при вершине Е равны как вертикальные; стороны DE и EA равны по построению (как половинки стороны AD); углы GDE и BAE равны как накрест лежащие при пересечении параллельных оснований трапеции секущей боковой стороной AD. Значит, треугольники равны по второму признаку.

Значит, равны и их соответственные стороны AB и GD — они обе помечены буквой a. А средняя линия трапеции — отрезок EF — теперь одновременно является средней линией треугольника GBC, и, следовательно, отрезок EF параллелен основанию GC и равен половине основания GC.

А основание GC содержит основание трапеции CD, то есть средняя линия трапеции параллельна основаниям трапеции. 

И также отрезок GC равен сумме оснований трапеции a+b, значит, средняя линия EF равна половине этого суммы оснований трапеции EF = (a + b) / 2. 

Что и требовалось доказать.

Задача с применением свойства средней линии трапеции

Задача: 

В трапеции ABCD основания AD = 14 см, BC = 8 см. Боковые стороны AB = 7 см, CD = 5 см. Найдите длину средней линии и периметр трапеции.

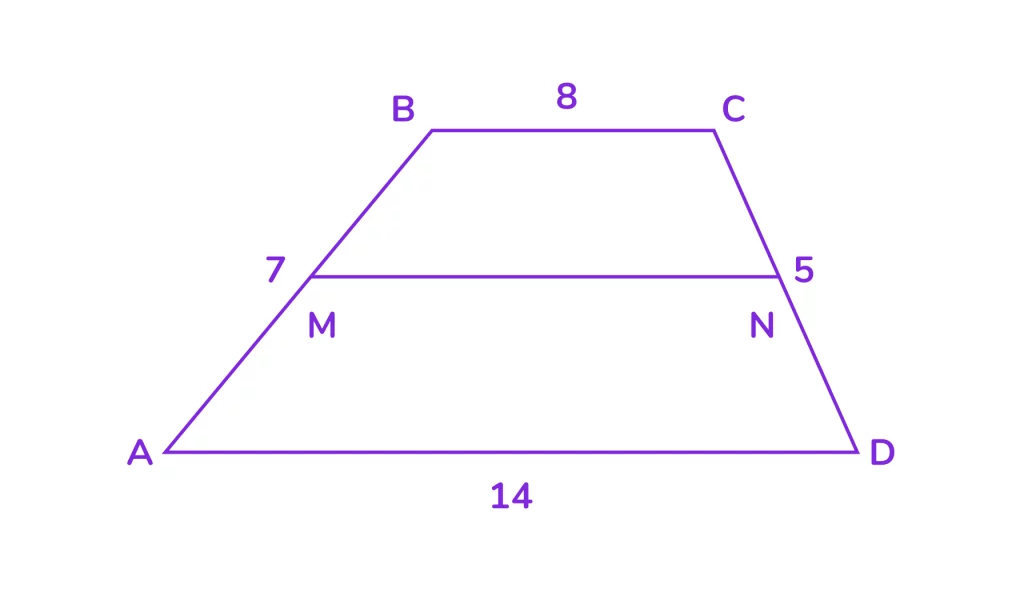
Решение:

1. Найдём длину средней линии MN.
По доказанной теореме:
MN = (AD + BC)/2 = (14 + 8)/2 = 22/2 = 11 см.

2. Найдём периметр трапеции.
Периметр — это сумма длин всех сторон:
P = AB + BC + CD + AD = 7 + 8 + 5 + 14 = 34 см.

Ответ: Длина средней линии 11 см, периметр трапеции 34 см.

📝 Задание для самопроверки

А теперь попробуйте решить задание по этой теме самостоятельно.

Задание 

В трапеции ABCD основания AD=14 см и CB=6 см. Найдите длину средней линии трапеции.

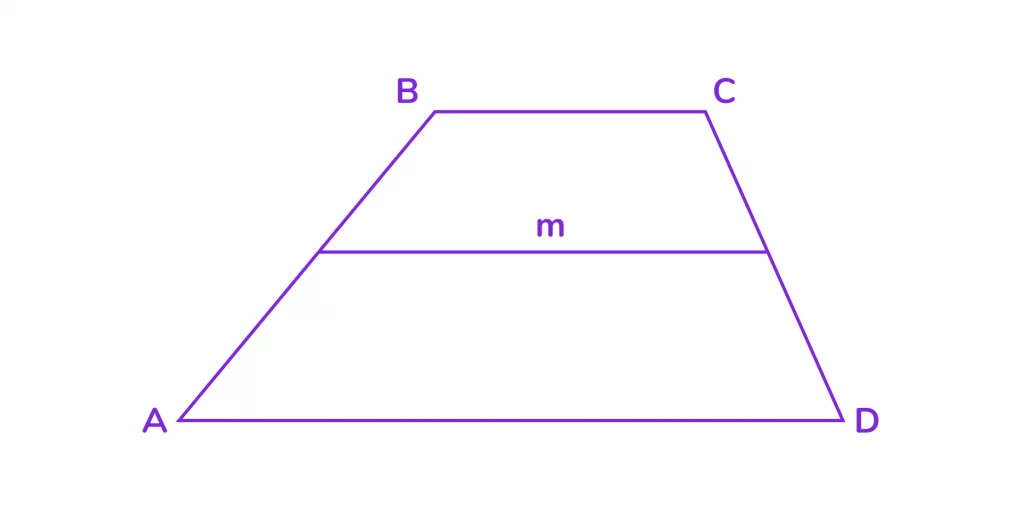
Решение: Средняя линия m=(14+6)/2=20/2=10 см.

Ответ: Средняя линия равна 10 см.

Подведём итоги

Мы изучили важное геометрическое понятие — среднюю линию трапеции — и узнали:

1. Определение. Средняя линия соединяет середины боковых сторон трапеции.
2. Основное свойство средней линии трапеции. Она параллельна основаниям и равна их полусумме.
3. Практическое применение. Использование при решении задач на вычисление длин.