Смежные и вертикальные углы

В школьной программе изучение углов начинается в 7-м классе. Углы — это важный элемент геометрии, обладающий множеством полезных свойств, которые делают его изучение необходимым для понимания геометрии в целом. В этой статье мы подробно разберём смежные и вертикальные углы, их определение и свойства, докажем основную теорему о смежных углах, а также научимся решать задачи с их использованием.

Определение смежных и вертикальных углов

Смежные углы — это два угла, у которых одна сторона общая, а две другие образуют прямую линию. Например, если на плоскости проведена прямая AB, а из точки O на этой прямой проведён луч ОС, то углы ∠AOC и ∠BOC будут смежными.

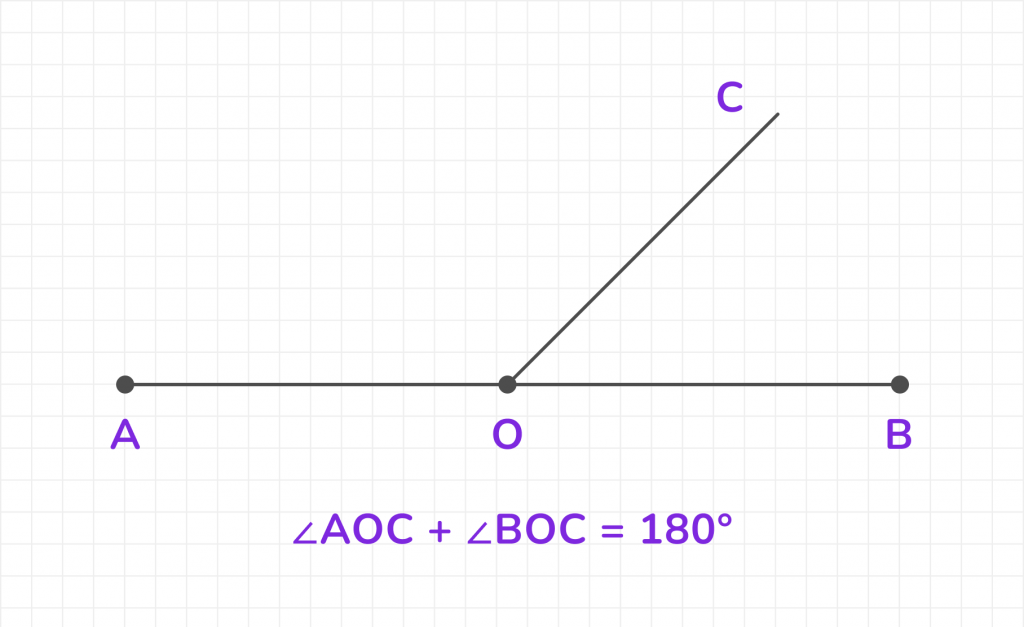
Свойства смежных углов:

1. Сумма смежных углов равна 180°. 
2. Если один из смежных углов острый (меньше 90°), то второй обязательно тупой (больше 90°).
3. Если один из смежных углов прямой (равен 90°), то второй также будет прямым.

Вертикальные углы возникают при пересечении двух прямых. Они представляют собой пары противоположно лежащих углов. Например, если прямые AB и CD пересекаются в точке O, то углы ∠AOC и ∠BOD являются вертикальными, как и углы ∠AOD и ∠BOC.

Свойства вертикальных углов:

1. Вертикальные углы равны.
2. При пересечении двух прямых образуется 4 угла, из которых 2 пары являются вертикальными.
3. Вертикальные углы могут быть острыми, тупыми или прямыми в зависимости от расположения прямых.

Теорема о смежных углах

Теорема: сумма смежных углов равна 180°.

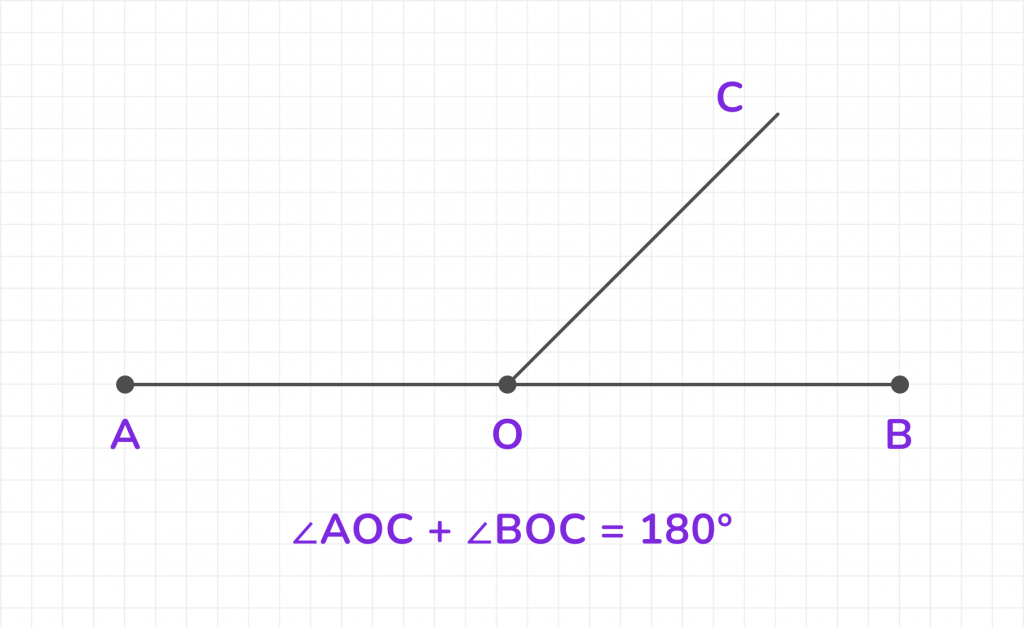
Доказательство:

1. Пусть на плоскости дана прямая AB, а из точки O на этой прямой проведён луч OC.
2. Образуются два угла: ∠AOC и ∠BOC.
3. По определению смежных углов, стороны OA и OB лежат на одной прямой, а сторона OC является общей.
4. Прямая AB представляет собой развёрнутый угол, который равен 180°.
5. Углы ∠AOC и ∠BOC вместе составляют этот развёрнутый угол.
6. Следовательно, ∠AOC + ∠BOC = 180°.

Теорема доказана.

Решение задач на смежные и вертикальные углы

Задача 1. Один из смежных углов равен 50°. Найдите второй угол.

Решение:

1. По теореме о смежных углах сумма смежных углов равна 180°.
2. Пусть первый угол равен 50°, а второй угол равен x.
3. Составляем уравнение: 50° + x = 180°.
4. Решаем уравнение: x = 180° − 50° = 130°.

Ответ: второй угол равен 130°.

Задача 2. Две прямые пересекаются в точке O. Угол ∠AOC = 70°. Найдите все остальные углы.

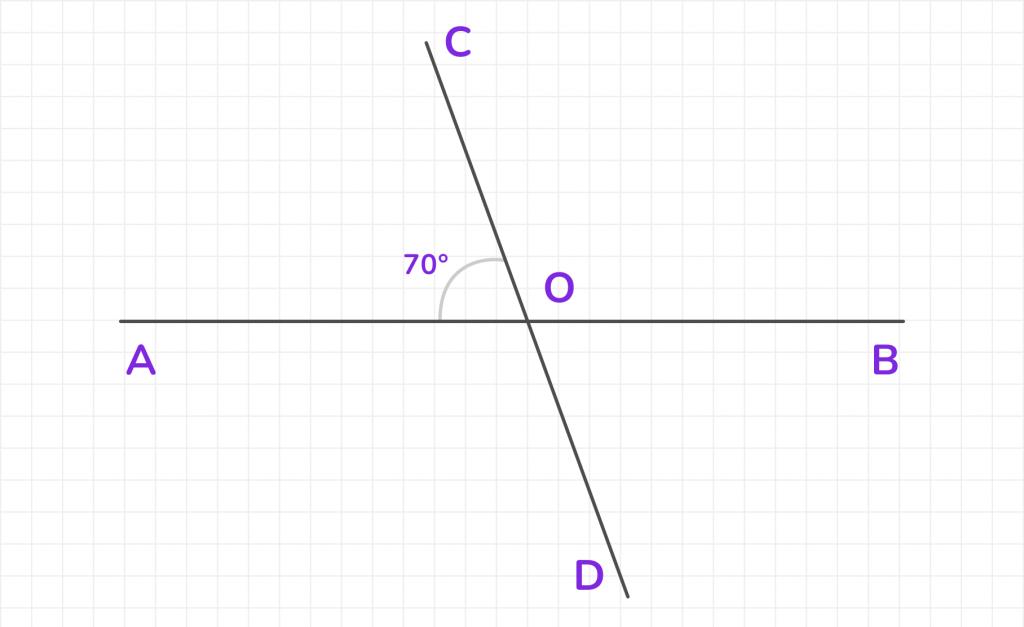
Решение:

1. При пересечении двух прямых образуется 4 угла: ∠AOC, ∠BOD, ∠AOD, ∠BOC.
2. Углы ∠AOC и ∠BOD являются вертикальными, следовательно, они равны: ∠BOD = 70°.
3. ∠AOD и ∠BOC также являются вертикальными углами и равны между собой.
4. ∠AOC и ∠AOD являются смежными углами, следовательно, их сумма равна 180°: ∠AOC + ∠AOD = 180°.
5. Подставляем известное значение: 70° + ∠AOD = 180°.
6. Находим ∠AOD = 180° − 70° = 110°.
7. Так как ∠AOD = ∠BOC, то ∠BOC = 110°.

Ответ: ∠AOC = 70°, ∠BOD = 70°, ∠AOD = 110°, ∠BOC = 110°.

Задача 3. Два вертикальных угла в сумме дают 140°. Найдите каждый угол.

Решение:

1. По свойству вертикальных углов они равны между собой.
2. Пусть каждый из вертикальных углов равен x.
3. Тогда их сумма равна: x + x = 140°.
4. Решаем уравнение: 2x = 140°, x = 70°.

Ответ: каждый из вертикальных углов равен 70°.

Задача 4. Два смежных угла равны 60° и 120°. Найдите угол между их биссектрисами.

Решение:

1. Биссектриса делит угол пополам. Следовательно, биссектриса первого угла делит его на два угла по 30°, а биссектриса второго угла делит его на два угла по 60°.
2. Угол между биссектрисами равен сумме половин каждого из углов: 30° + 60° = 90°.

Ответ: угол между биссектрисами равен 90°.

Смежные и вертикальные углы — это важные элементы геометрии, обладающие множеством полезных свойств. Изучение этих углов помогает ученикам 7-го класса лучше понять основы геометрии и подготовиться к более сложным задачам. Мы рассмотрели определения, доказали теорему о смежных углах, решили несколько задач и выяснили ключевые свойства смежных и вертикальных углов.

Если ребёнок испытывает трудности в работе со смежными и вертикальными углами, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия!