Решение систем уравнений: понятия и методы

Решение систем уравнений — это важный раздел математики, который изучается в 7–9-х классах. Системы уравнений помогают решать задачи, связанные с реальными ситуациями, например, нахождение неизвестных величин в экономике, физике и других науках. В этой статье мы разберём основные понятия, методы решения систем уравнений и научимся применять их на практике.

Основные понятия

📎 Уравнение

Уравнение — это математическое равенство, содержащее одну или несколько переменных.

Например:

1. 3 + x = 7 (уравнение с одной переменной x);
2. 2x + 3y = 6 (уравнение с двумя переменными x и y).

Решить уравнение означает найти такие значения переменных, которые обращают его в верное равенство.

📎 Система уравнений

Система уравнений — это совокупность двух или более уравнений, объединённых фигурной скобкой, для которых требуется найти значения переменных, удовлетворяющих всем уравнениям одновременно.

Пример:

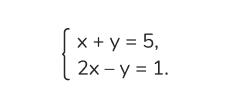
Основные характеристики:

1. Решение системы — это набор значений переменных (например, пара чисел x, y), которые при подстановке в каждое уравнение обращают его в верное равенство.

2. Система может иметь:

1. единственное решение;
2. бесконечно много решений;
3. ни одного решения.

Линейное уравнение с двумя переменными

Линейное уравнение с двумя переменными имеет вид:

ax + by = c,

где:

1. a, b, c — заданные числа (коэффициенты);
2. x и y — переменные.

Пример:
2x + 3y = 6.

Решением такого уравнения является пара чисел (x, y), которая обращает уравнение в верное равенство.

Система двух линейных уравнений с двумя переменными

Система двух линейных уравнений с двумя переменными записывается так:

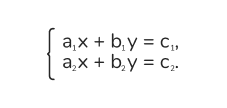
Решением системы является пара чисел (x, y), которая удовлетворяет обоим уравнениям одновременно.

Метод подстановки

Метод подстановки заключается в следующем:

1. Из одного уравнения выражаем одну переменную через другую.
2. Подставляем полученное выражение во второе уравнение.
3. Решаем уравнение с одной переменной.
4. Находим значение второй переменной.

Пример
Решить систему:

1. Из первого уравнения выразим y через x:
y = 5 — x.

2. Подставим y = 5 — x во второе уравнение:
2x — (5 — x) = 1.

3. Упростим и решим уравнение:
2x — 5 + x = 1;
3x = 6;
x = 2.

4. Найдём y:
y = 5 — x = 5 — 2 = 3.

Ответ: (x, y) = (2, 3).

Метод сложения

Метод сложения используется для устранения одной из переменных путём сложения или вычитания уравнений.

Алгоритм:

1. Умножьте одно или оба уравнения на такие числа, чтобы коэффициенты при одной из переменных стали равны по модулю.
2. Сложите или вычтите уравнения, чтобы исключить эту переменную.
3. Решите полученное уравнение с одной переменной.
4. Найдите значение второй переменной.

Пример
Решить систему:

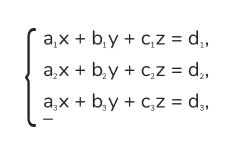
1. Коэффициенты при y уже равны по модулю (2 и -2). Сложим уравнения:
(3x + 2y) + (x — 2y) = 8 + 4;
4x = 12;
x = 3.

2. Подставим x = 3 в первое уравнение:
3 ∙ 3 + 2y = 8;
9 + 2y = 8;
2y = -1;
y = -0,5.

Ответ: (x, y) = (3, -0,5).

Система линейных уравнений с тремя переменными

Система трёх линейных уравнений с тремя переменными записывается так:

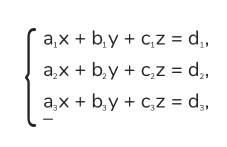
Для решения таких систем используют методы:

1. Подстановки: выражают одну переменную через другие и подставляют в остальные уравнения.
2. Сложения: исключают одну переменную, приводя систему к двум уравнениям с двумя переменными.

Пример
Решить систему:

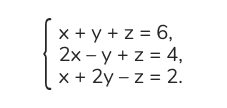
1. Сложим первое и третье уравнения:
(x + y + z) + (x + 2y — z) = 6 + 2;
2x + 3y = 8.

2. Сложим первое и второе уравнения:
(x + y + z) + (2x — y + z) = 6 + 4;
3x + 2z = 10.

3. Теперь решаем систему из двух уравнений:

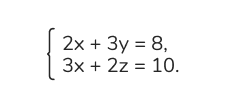
4. Выразим y из первого уравнения:
y = (8 — 2x) / 3.

5. Подставим y во второе уравнение и найдём x, z.

Ответ: (x, y, z) = (2, 2, 2).

Решение задач

📌 Задача 1

На складе хранятся яблоки и груши. Всего 150 кг фруктов. Яблок в два раза больше, чем груш. Сколько килограммов яблок и груш на складе?

Решение
Пусть x — количество груш, y — количество яблок.
Составим систему уравнений:

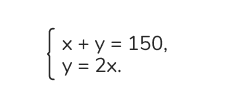
1. Подставим y = 2x в первое уравнение:
x + 2x = 150;
3x = 150;
x = 50.

2. Найдём y:
y = 2x = 2 ∙ 50 = 100.

Ответ: груш — 50 кг, яблок — 100 кг.

📌 Задача 2

Ученик купил карандаши и ручки. Всего он потратил 70 рублей, а количество предметов составило 10 штук. Карандаш стоит 5 рублей, а ручка –– 10 рублей. Сколько карандашей и ручек купил ученик?

Решение

1. Обозначим:

x — количество карандашей;

y — количество ручек.

2. Составим систему уравнений:

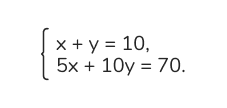
3. Из первого уравнения выразим y через x: y = 10 — x.

4. Подставим y = 10 — x во второе уравнение: 5x + 10(10 — x) = 70.

5. Упростим:

5x + 100 — 10x = 70;

-5x + 100 = 70;

-5x = -30,

x = 6.

6. Найдём y: y = 10 — x = 10 — 6 = 4.

Ответ: ученик купил 6 карандашей и 4 ручки.

Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы!