Равноускоренное движение

Равноускоренное движение — это фундаментальная концепция в курсе физики 9-го класса, которая раскрывает законы движения тел с постоянным ускорением и находит широкое применение в механике, астрономии и других научных дисциплинах. В этой статье мы разберём основные определения, формулы, графики и примеры решения задач, связанных с равноускоренным движением.

Основные определения

📎 Ускорение

Ускорение — это физическая величина, которая характеризует быстроту изменения скорости тела. Иными словами, ускорение показывает, насколько изменяется скорость тела за каждую секунду. Если тело увеличивает свою скорость, то ускорение будет положительным, а если замедляется — отрицательным.

Формула для расчёта ускорения записывается так:

a = (V — V₀) / t

где:

1. a — ускорение [м/с²];
2. V — конечная скорость тела [м/с];
3. V₀ — начальная скорость тела [м/с];
4. t — время, за которое происходит изменение скорости [с].

📎 Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение — это такое движение, при котором тело движется по прямой линии, а его скорость изменяется на одну и ту же величину за равные промежутки времени. Это означает, что ускорение остаётся постоянным на всем пути движения.

Примеры равноускоренного движения встречаются в повседневной жизни:

1. Автомобиль, который разгоняется или тормозит на прямой дороге.
2. Лыжник, скатывающийся с горы с постоянным ускорением.
3. Свободное падение тела под действием силы тяжести (например, камень, брошенный с высоты).

📎 Равномерное движение как частный случай

Если ускорение равно нулю (a = 0), то движение становится равномерным. Это означает, что тело движется с постоянной скоростью, не изменяя её ни по величине, ни по направлению. В таком случае перемещение тела можно рассчитать по формуле: 

S = V · t 

где:

1. S — перемещение тела [м];
2. V — постоянная скорость тела [м/с];
3. t — время движения [с].

График зависимости скорости от времени при равноускоренном движении

График зависимости скорости от времени при равноускоренном движении представляет собой прямую линию, так как скорость изменяется равномерно с течением времени. Уравнение этой зависимости записывается в виде:

V(t) = V₀ + a · t

где:

1. V(t) — скорость тела в момент времени t [м/с];
2. V₀ — начальная скорость тела [м/с];
3. a — ускорение [м/с²];
4. t — время [с].

График начинается с точки, соответствующей начальной скорости V₀. Если начальная скорость равна нулю (V₀ = 0), то график начинается из начала координат.

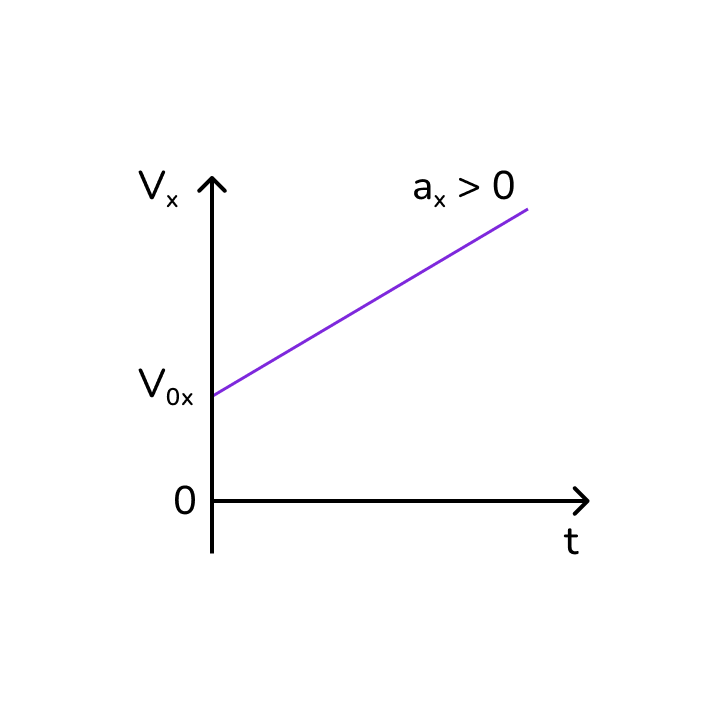
Угол наклона прямой к оси времени зависит от величины ускорения a. Чем больше ускорение, тем круче поднимается (или опускается) график:

1. При положительном ускорении (a > 0) график возрастает.
2. А при отрицательном ускорении (a < 0) — убывает.

Пример ⤵︎

Пусть тело начинает движение с начальной скоростью V₀ = 5 м/с и движется с ускорением a = 2 м/с². Зависимость скорости от времени будет описываться формулой:

V(t) = 5 + 2 · t

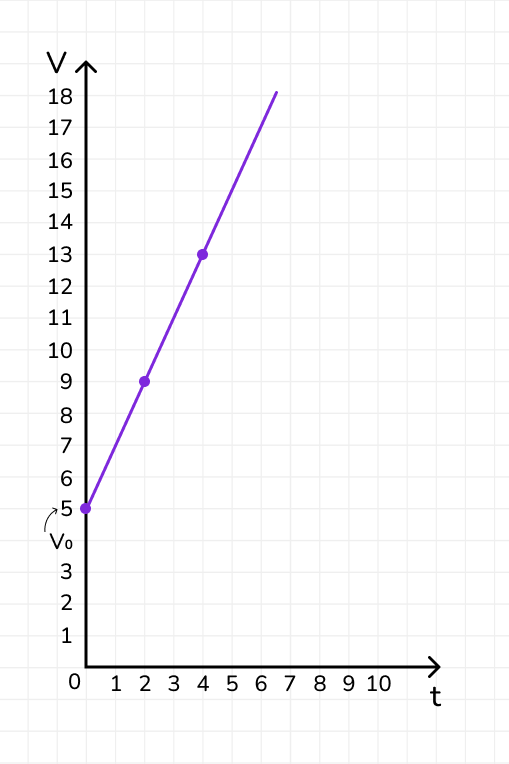
Для построения графика:

1. При t = 0, скорость V(0) = 5 м/с.
2. При t = 2, скорость V(2) = 5 + 2 · 2 = 9 м/с.
3. А если t = 4, скорость V(4) = 5 + 2 · 4 = 13 м/с.

Точки (0, 5), (2, 9) и (4, 13) соединяются прямой линией, что и даёт график зависимости скорости от времени.

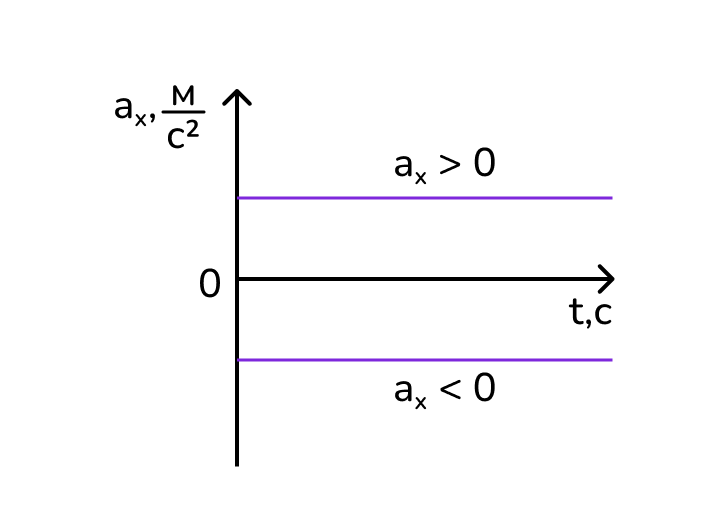
Если ускорение равно нулю (a = 0), график становится горизонтальной прямой, так как скорость остаётся постоянной.

При свободном падении тела ускорение равно ускорению свободного падения (g ≈ 9,8 м/с²), и график также представляет собой прямую линию.

Перемещение при равноускоренном движении

📎 Перемещение — это векторная величина, которая характеризует изменение положения тела в пространстве. При равноускоренном движении перемещение можно рассчитать с помощью формул, учитывающих начальную скорость, ускорение и время движения.

Формула для перемещения при равноускоренном движении записывается так:

S = V₀ · t + (a · t²) / 2

где:

1. S — перемещение [м];
2. V₀ — начальная скорость [м/с];
3. a — ускорение [м/с²];
4. t — время движения [с].

Если начальная скорость равна нулю (V₀ = 0), формула упрощается:

S = (a · t²) / 2

1. Случай с начальной скоростью

Если тело имеет начальную скорость V₀, то площадь под графиком складывается из:

1. прямоугольника с площадью V₀ · t (перемещение за счёт начальной скорости);
2. треугольника с площадью (a · t²) / 2 (перемещение за счёт ускорения).

2. Случай без начальной скорости

Если начальная скорость равна нулю (V₀ = 0), то площадь под графиком — это только треугольник:

S = (a · t²) / 2.

📌 Примеры расчёта перемещения

Пример 1
Тело начинает движение с начальной скоростью V₀ = 4 м/с и ускорением a = 3 м/с². Найдите перемещение через t = 5 с.

Решение:
Используем формулу:
S = V₀ · t + (a · t²) / 2.
Подставляем значения:
S = 4 · 5 + (3 · 5²) / 2 = 20 + (3 · 25) / 2 = 20 + 75 / 2 = 20 + 37,5 = 57,5 м.
Ответ: 57,5 м.

Пример 2
Тело начинает движение без начальной скорости (V₀ = 0) с ускорением a = 2 м/с². Найдите перемещение через t = 6 с.

Решение:
Используем упрощенную формулу:
S = (a · t²) / 2.
Подставляем значения:
S = (2 · 6²) / 2 = (2 · 36) / 2 = 72 / 2 = 36 м.
Ответ: 36 м.

Графики равноускоренного движения 

Математически зависимость координаты от времени при равноускоренном движении описывается квадратичной функцией, её график — парабола. Формула зависимости координаты от времени записывается так:

x(t) = x₀ + V₀ · t + (a · t²) / 2

где:

1. x(t) — координата тела в момент времени t [м];
2. x₀ — начальная координата тела [м];
3. V₀ — начальная скорость тела [м/с];
4. a — ускорение тела [м/с²];
5. t — время [с].

График этой зависимости представляет собой параболу. Если ускорение положительное (a > 0), ветви параболы направлены вверх. Если ускорение отрицательное (a < 0), ветви параболы направлены вниз. Форма графика наглядно показывает, как координата тела изменяется с течением времени.

Например, в начале движения влияние квадратичного члена (a · t²) / 2 может быть небольшим, и график близок к линейному. По мере увеличения времени квадратичный член начинает доминировать, и график становится более криволинейным.

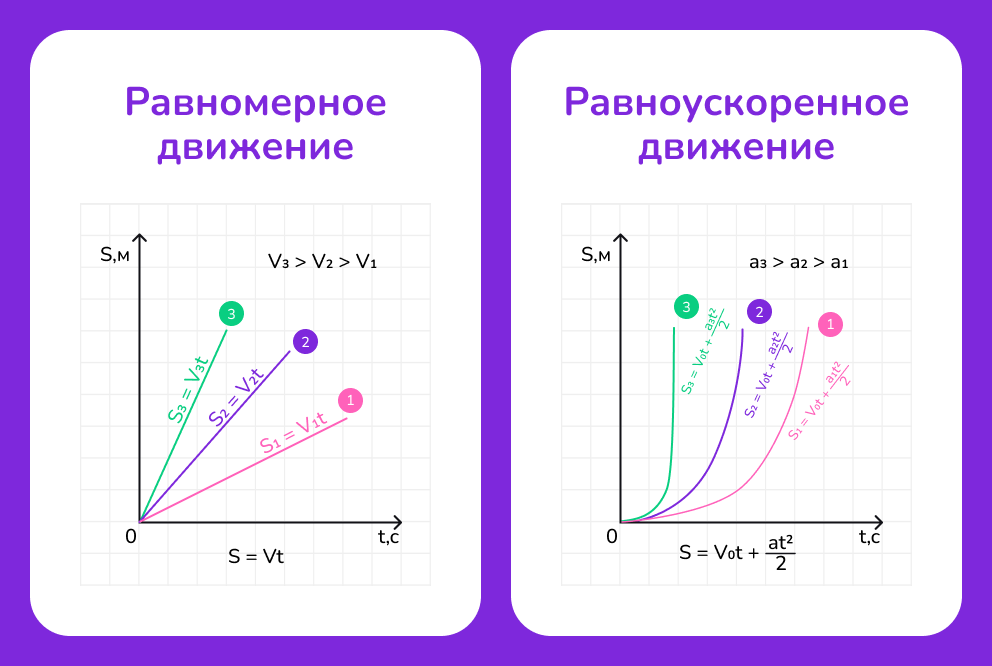
Решение задач

Задача 1. Тело начинает движение с начальной скоростью V₀ = 4 м/с и движется с ускорением a = 2 м/с². Найдите скорость тела через t = 6 с.

Решение: 

Используем формулу зависимости скорости от времени:
V(t) = V₀ + a · t.
Подставляем известные значения:
V(6) = 4 + 2 · 6 = 4 + 12 = 16 м/с.
Ответ: 16 м/с.

Задача 2. Тело движется с начальной скоростью V₀ = 3 м/с и ускорением a = 1.5 м/с². Найдите перемещение тела за время t = 8 с.

Решение: 

Используем формулу перемещения:
S = V₀ · t + (a · t²) / 2.
Подставляем известные значения:
S = 3 · 8 + (1.5 · 8²) / 2 = 24 + (1.5 · 64) / 2 = 24 + 96 / 2 = 24 + 48 = 72 м.
Ответ: 72 м.

Задача 3. Тело начинает движение из состояния покоя (V₀ = 0) с ускорением a = 5 м/с². Через какое время тело пройдет путь S = 100 м?

Решение:

Используем формулу перемещения для случая, когда начальная скорость равна нулю:
S = (a · t²) / 2.
Выразим время t:
t² = (2 · S) / a,
t = √((2 · S) / a).
Подставляем известные значения:
t = √((2 · 100) / 5) = √(200 / 5) = √40 ≈ 6,32 с.
Ответ: ≈ 6,32 с.

---

Равноускоренное движение — это фундаментальное понятие в физике, которое помогает понять, как тела движутся с постоянным ускорением. Мы разобрали основные характеристики такого движения: скорость, перемещение и координаты тела, а также научились строить графики, которые наглядно демонстрируют изменения этих величин с течением времени. Изучение равноускоренного движения закладывает основу для освоения более сложных тем механики и даёт важные навыки для решения реальных задач. 

Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы. Первый урок по форме ниже — бесплатный!