Прямоугольный треугольник    

В школьной программе изучение треугольников начинается в 7–8-х классах, особое внимание уделяется фигуре — прямоугольный треугольник. Это важная геометрическая фигура, обладающая множеством полезных свойств и признаков, которые делают её изучение ключевым для понимания геометрии в целом.

В этой статье мы подробно разберём определение прямоугольного треугольника, его свойства, основные формулы, теорему Пифагора, а также научимся решать задачи с использованием этих знаний.

Определение прямоугольного треугольника

Прямоугольный треугольник — это треугольник, у которого один из углов равен 90° (прямой угол). Стороны, образующие прямой угол, называются катетами, а сторона, лежащая напротив прямого угла, называется гипотенузой.

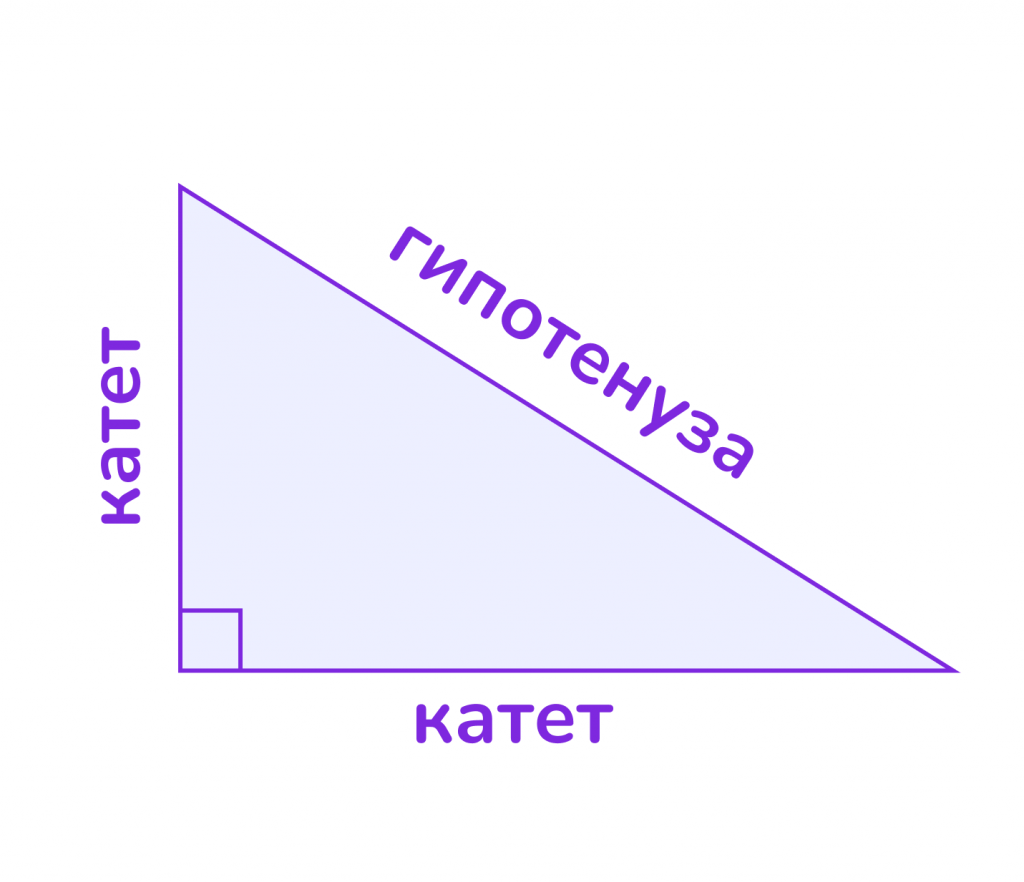
Ключевые элементы:

1. Катеты: две стороны, образующие прямой угол.
2. Гипотенуза: самая длинная сторона, противолежащая прямому углу.

Свойства прямоугольного треугольника

1️⃣ Сумма острых углов равна 90°. Если в треугольнике один угол равен 90°, то сумма двух других углов всегда равна 90°. Например, если один острый угол равен 30°, то второй будет 60°.

2️⃣ Гипотенуза больше любого из катетов. Гипотенуза является самой длинной стороной в прямоугольном треугольнике.

3️⃣ Теорема о высоте. Высота, проведённая из вершины прямого угла на гипотенузу, делит треугольник на два подобных ему треугольника. Эти треугольники также подобны исходному треугольнику.

4️⃣ Равенство треугольников. Прямоугольные треугольники равны, если их катеты равны или если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника.

5️⃣ Медиана, проведённая к гипотенузе. Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы. Это свойство позволяет построить окружность, описанную вокруг прямоугольного треугольника, где гипотенуза является диаметром.

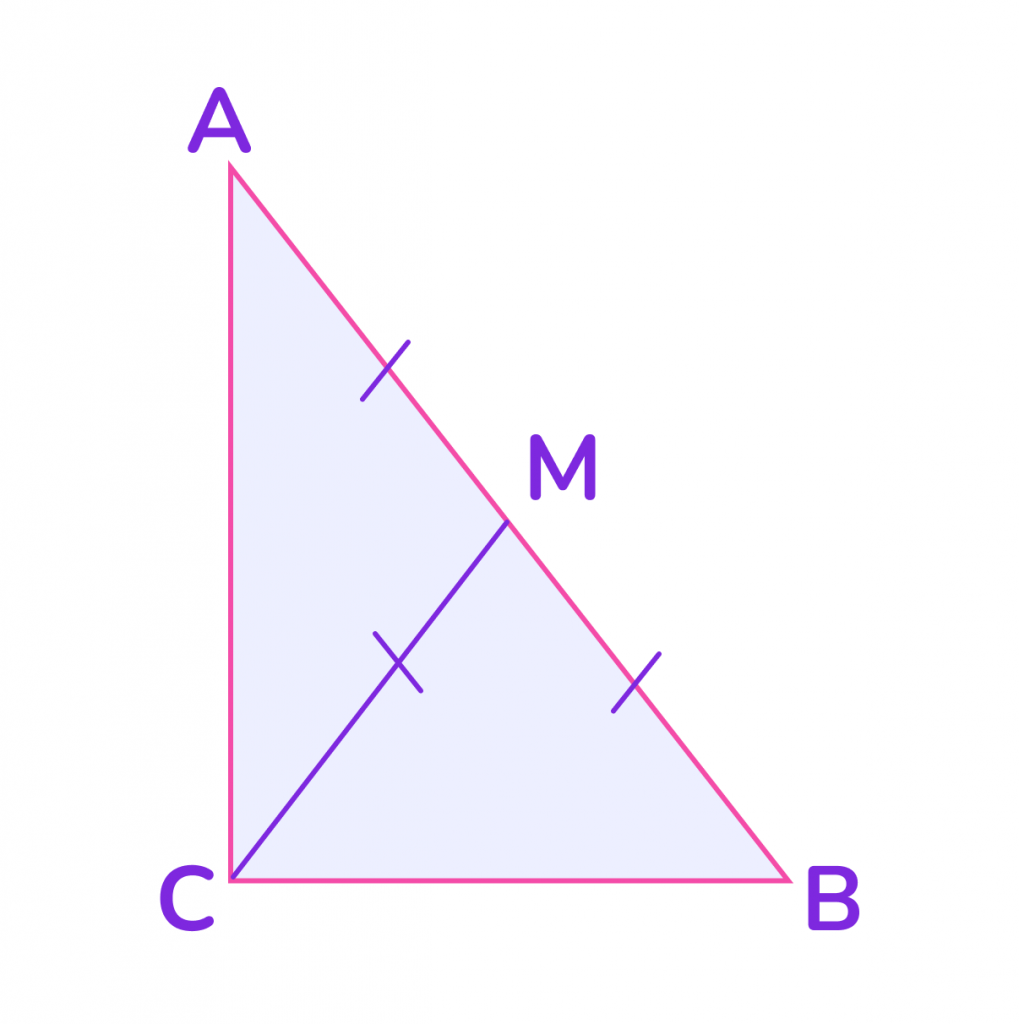
6️⃣ Отношение сторон в треугольнике с углами 30°, 60° и 90°.

Если один из острых углов равен 30°, то катет, лежащий напротив этого угла, равен половине гипотенузы. Например, если гипотенуза равна c, то катет, лежащий напротив угла 30°, равен c/2.

7️⃣ Синус, косинус и тангенс острых углов. В прямоугольном треугольнике синус, косинус и тангенс острых углов выражаются через отношения сторон:

8️⃣ Соотношение между сторонами и углами. Если известны длины сторон, можно найти углы с помощью тригонометрических функций и наоборот.

9️⃣ Подобие прямоугольных треугольников. Два прямоугольных треугольника подобны, если их острые углы равны. Это свойство часто используется при решении задач на подобие.

🔟 Центр описанной окружности. Центр окружности, описанной вокруг прямоугольного треугольника, находится в середине гипотенузы. Это следует из того, что гипотенуза является диаметром описанной окружности.

1️⃣1️⃣ Радиус описанной окружности. Радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы:

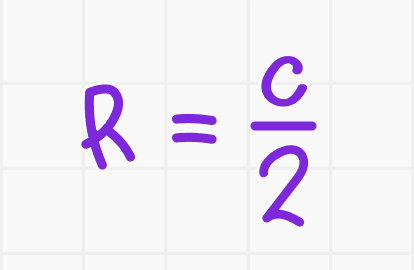
где с — длина гипотенузы. 

1️⃣2️⃣ Центр вписанной окружности. Центр окружности, вписанной в прямоугольный треугольник, находится на пересечении биссектрис всех трёх углов. Расстояние от центра до любой стороны равно радиусу вписанной окружности.

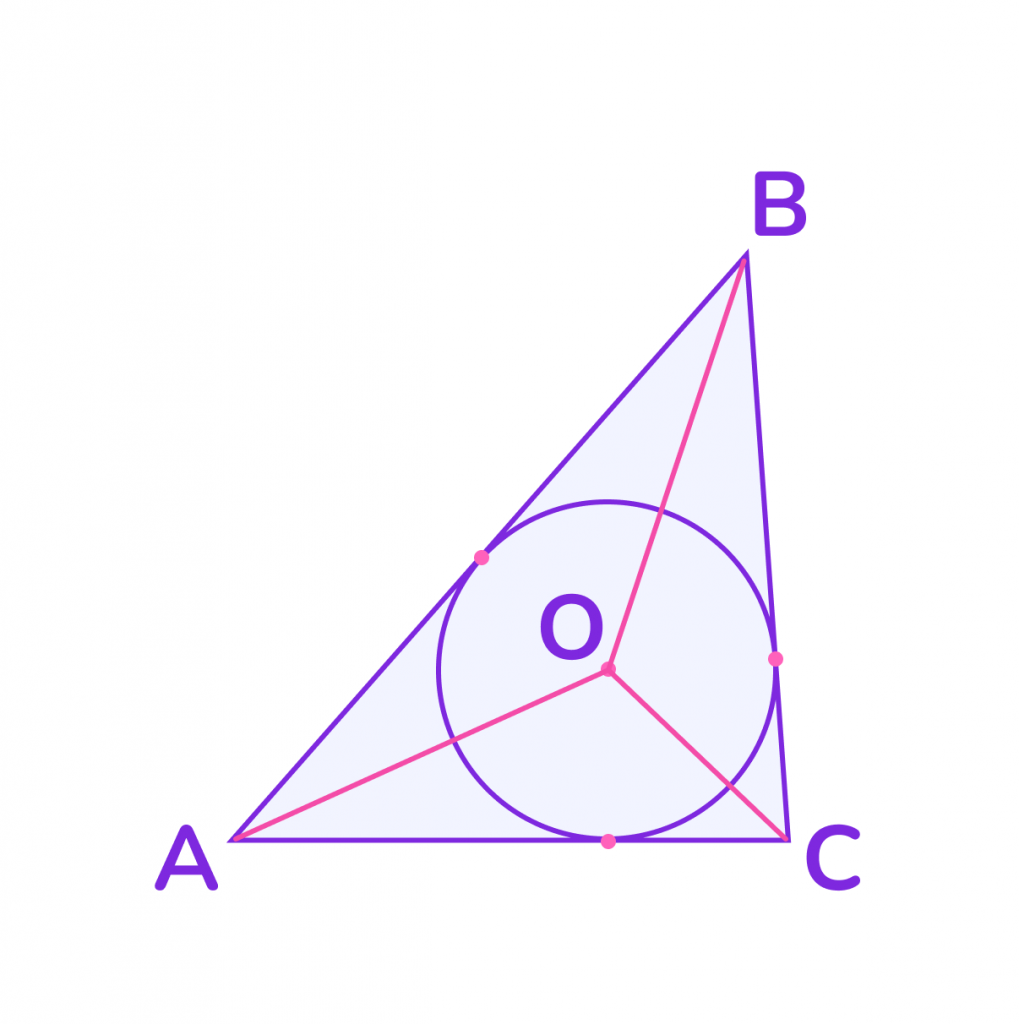
1️⃣3️⃣ Радиус вписанной окружности. Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле:

где a и b — катеты, c — гипотенуза.

Основные формулы

Теорема Пифагора

Теорема Пифагора — одна из самых важных теорем в геометрии, устанавливающая зависимость между сторонами прямоугольного треугольника.

Формулировка: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Формула: если a и b — длины катетов прямоугольного треугольника, а c — длина гипотенузы, то 

Доказательство:

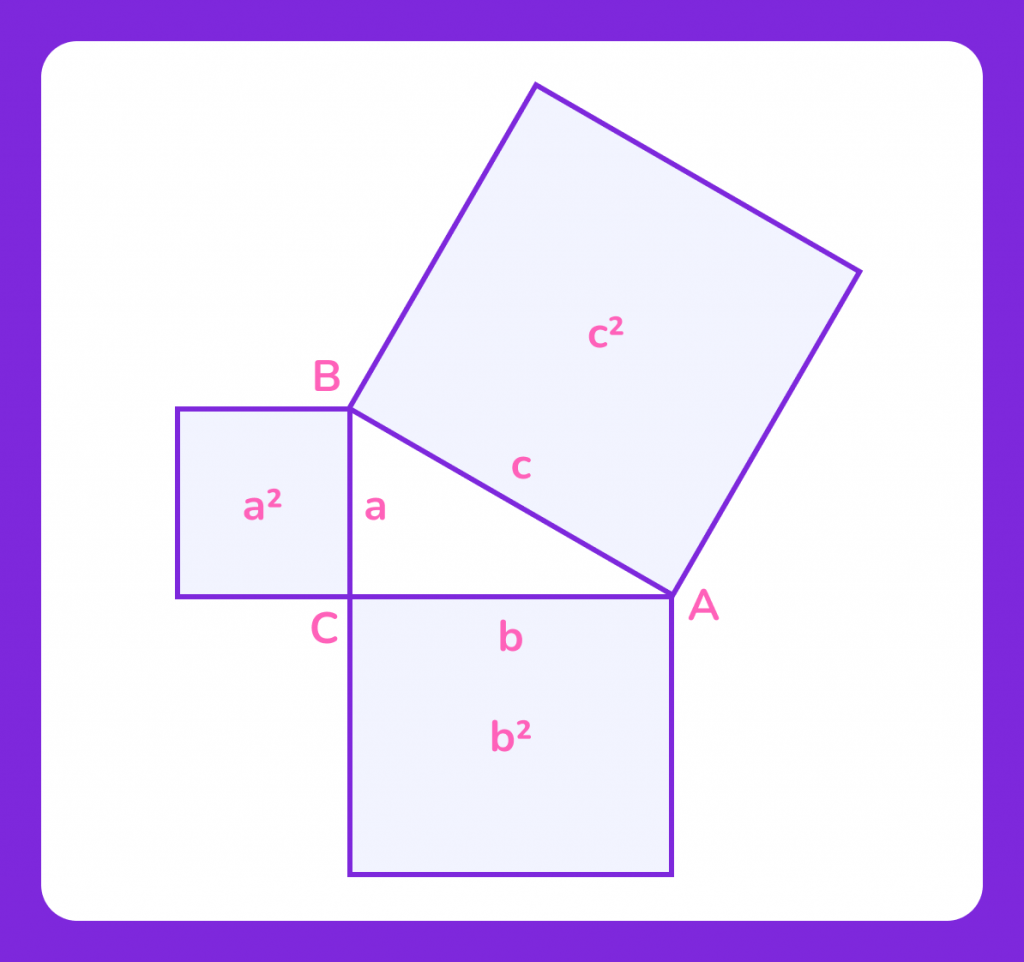
1. Построение квадрата на сторонах треугольника: построим квадрат на каждой из сторон прямоугольного треугольника. Площадь квадрата на гипотенузе будет равна c², а площади квадратов на катетах будут равны a² и b².

2. Разбиение квадрата на прямоугольники и треугольники: для доказательства теоремы Пифагора часто используется метод, основанный на разбиении и перестановке фигур. Рассмотрим квадрат, у которого стороны равны a + b. Этот квадрат можно разбить на три части, а именно: четыре одинаковых прямоугольных треугольника с катетами a и b и один маленький квадрат, который находится в середине.

3. Площадь большого квадрата со стороной a + b равна: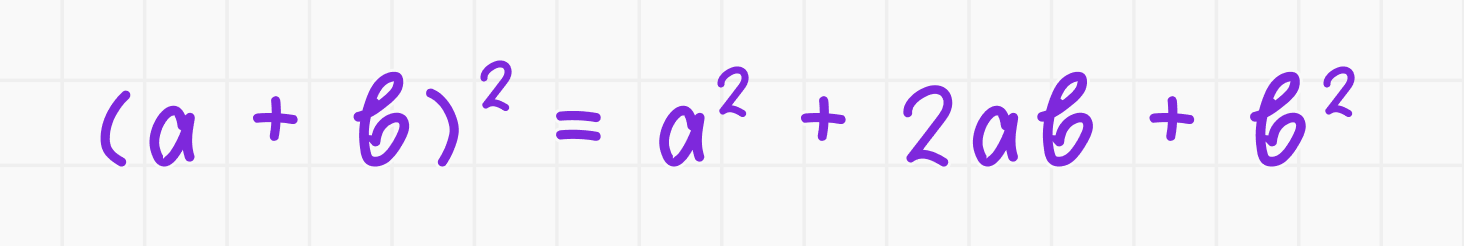

4. Площадь четырёх треугольников и маленького квадрата: площадь четырёх прямоугольных треугольников с катетами a и b равна: 

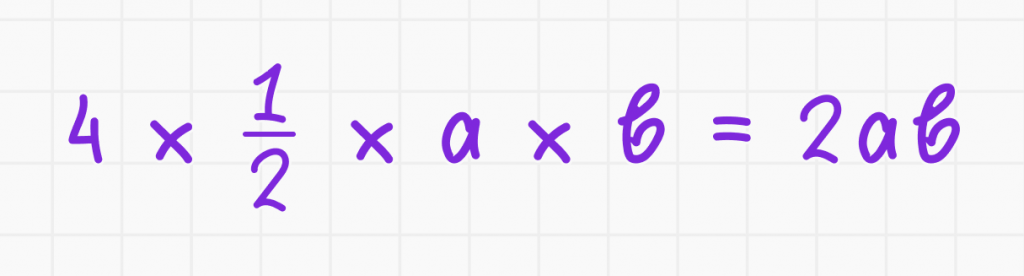
А площадь маленького квадрата равна c², где c — гипотенуза.

5. Сравнение площадей: площадь большого квадрата можно выразить как сумму площадей четырёх треугольников и маленького квадрата. Подставляя значения, получаем: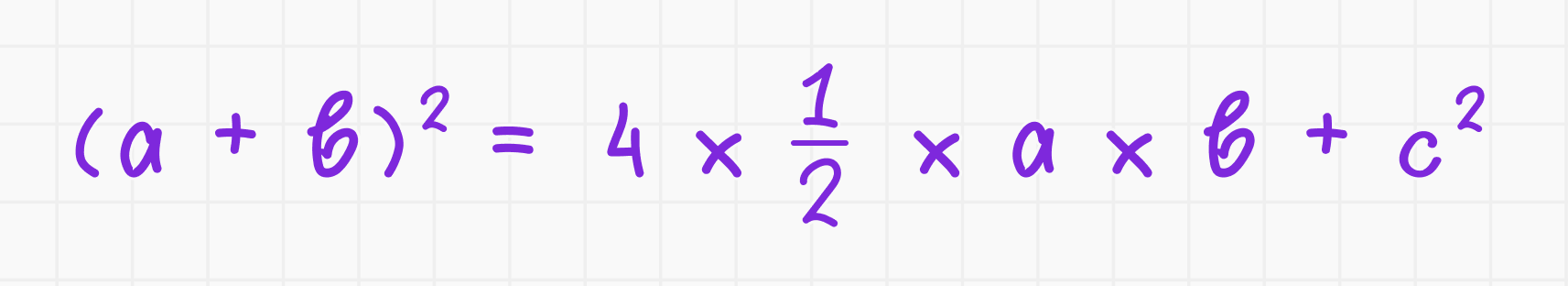

Упрощая, получаем:

Это и является доказательством теоремы Пифагора.

Формулы для всех сторон:

1. Нахождение гипотенузы (c):

2. Нахождение катета (a):

3. Нахождение катета (b):

Площадь и периметр прямоугольного треугольника

Площадь — это числовая характеристика, которая показывает, сколько места занимает фигура на плоскости. Для прямоугольного треугольника площадь можно вычислить несколькими способами в зависимости от известных данных. А именно:

— Основная формула через катеты

Площадь прямоугольного треугольника равна половине произведения его катетов:

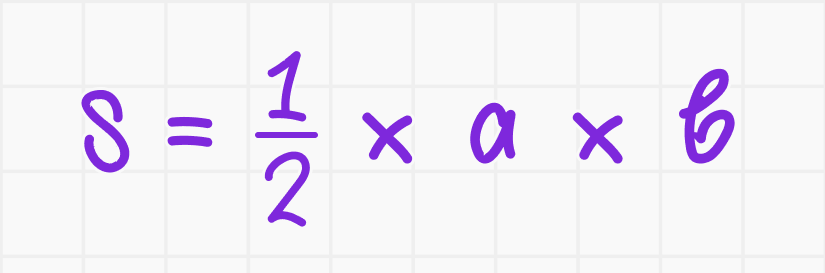
где a и b — длины катетов.

— Формула через гипотенузу и высоту

Если известна гипотенуза c и высота h, проведённая к ней, то площадь можно найти по формуле:

— Формула через радиус вписанной окружности 

Если известен радиус r вписанной окружности и полупериметр p, то площадь можно вычислить как:

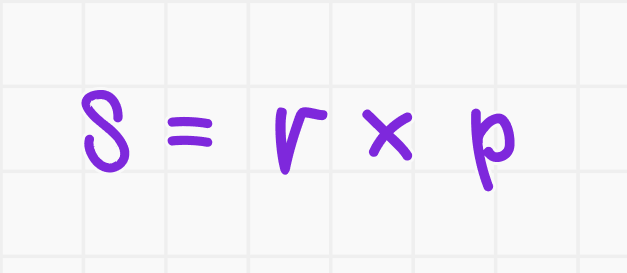
— Периметр прямоугольного треугольника

Периметр — это сумма длин всех сторон треугольника. Для прямоугольного треугольника периметр вычисляется по формуле:

где: a и b — катеты, c — гипотенуза.

— Связь между площадью и периметром

Площадь и периметр прямоугольного треугольника связаны через его стороны. Например, если известны две стороны (катеты или катет и гипотенуза), можно сначала вычислить третью сторону (по теореме Пифагора), затем найти периметр и площадь.

Особые случаи

— Равнобедренный прямоугольный треугольник

Если катеты равны (a = b), то:

1. Площадь:

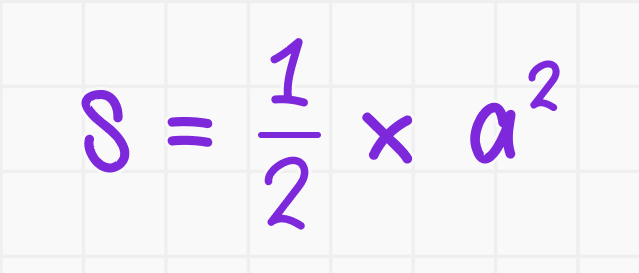
2. Гипотенуза:

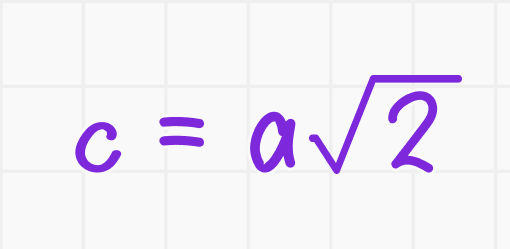
3. Периметр:

— Треугольник с углами 30°, 60° и 90°

Если один из острых углов равен 30°, то:

1. Катет, лежащий напротив угла 30°, равен половине гипотенузы:

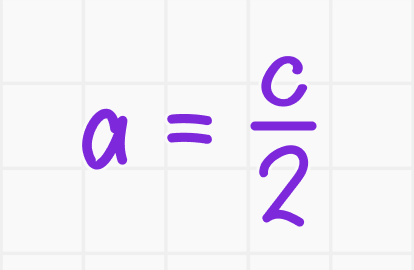
2. Второй катет:

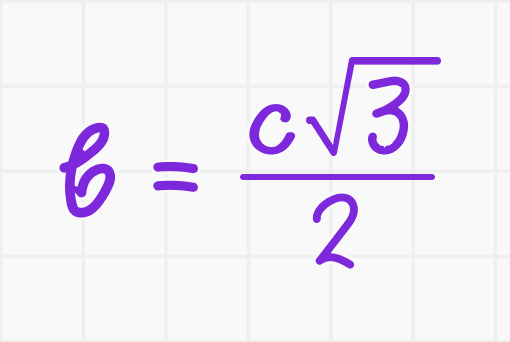
3. Площадь:

Решение задач с прямоугольными треугольниками

Задача 1

Дано: прямоугольный треугольник с гипотенузой c = 10 и катетом a = 6.

Найдите: второй катет b.

Решение: используем теорему Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

Выразим b² из формулы:

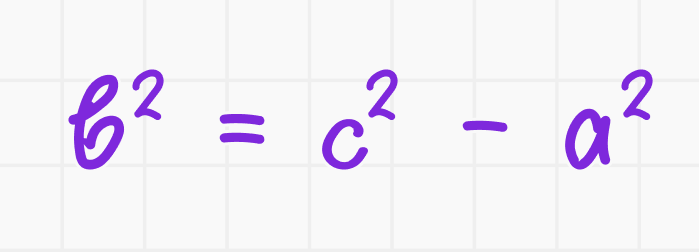
Подставляем известные значения:

Находим b, извлекая квадратный корень:

Ответ: b = 13.

Задача 2

Дано: прямоугольный треугольник с катетами a = 5 и b = 12.

Найдите: гипотенузу c.

Решение: используем теорему Пифагора:

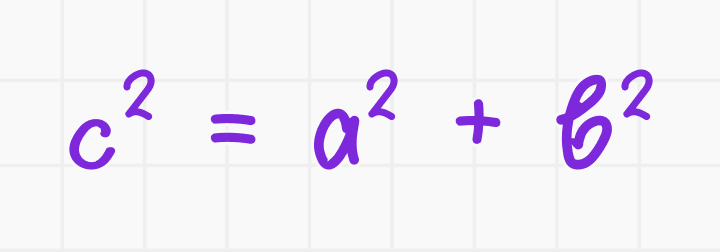
Подставляем известные значения:

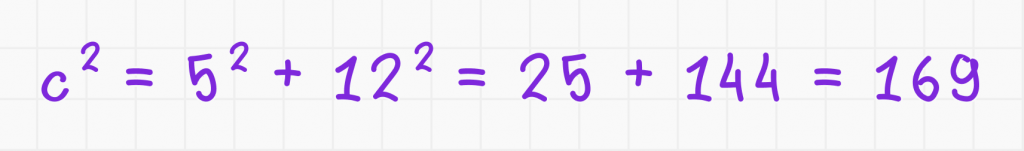
Находим c, извлекая квадратный корень:

Ответ: c = 13.

Задача 3

Дано: прямоугольный треугольник с катетами a = 9 и b = 12.

Найдите: периметр треугольника P.

Решение. Сначала найдём гипотенузу c по теореме Пифагора:

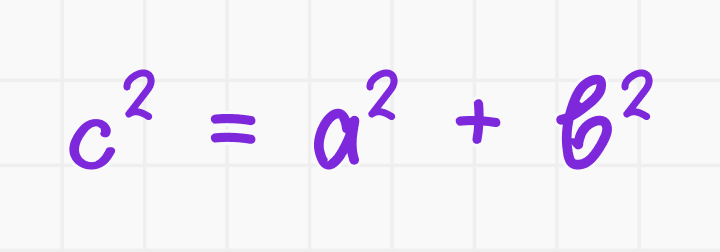
Подставляем значения:

Находим c:

Периметр треугольника вычисляется как сумма всех сторон:

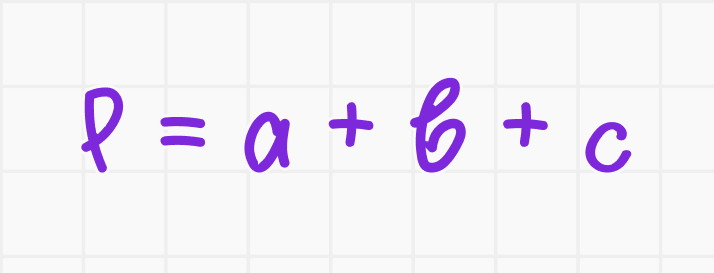
Подставляем значения:

Ответ: P = 36.

Задача 4

Дано: прямоугольный треугольник с катетами a = 8 и b = 15.

Найдите: площадь треугольника S.

Решение. Площадь прямоугольного треугольника вычисляется по формуле:

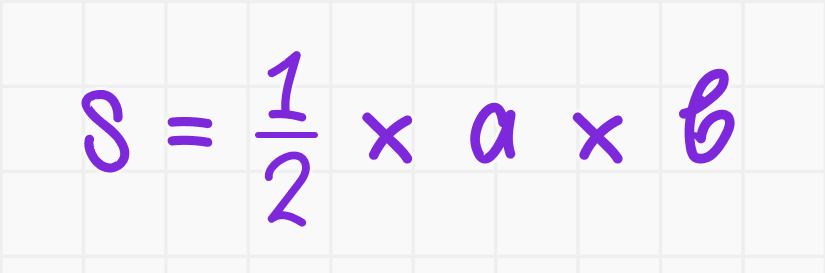
Подставляем известные значения:

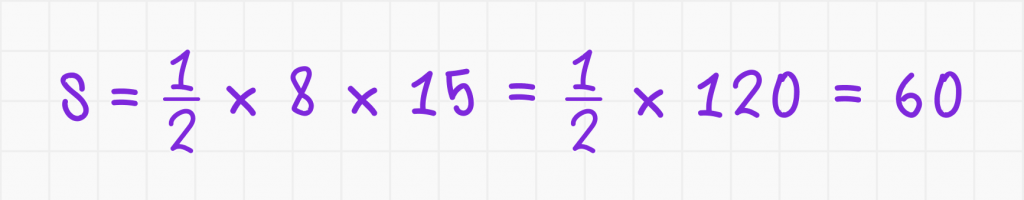
Ответ: S = 60.

Прямоугольный треугольник — это важная геометрическая фигура, которая обладает множеством полезных свойств. Изучение прямоугольных треугольников помогает ученикам 7–8-х классов лучше понять основы геометрии и подготовиться к более сложным задачам. Мы рассмотрели определение, свойства, основные формулы, теорему Пифагора, площадь и периметр прямоугольного треугольника, а также решили несколько задач.

Если ребёнок испытывает трудности в работе с прямоугольными треугольниками, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия!