
Прямая и обратная пропорциональные зависимости
Пропорциональные зависимости — это важная тема математики 6 класса, которая помогает понять, как изменяются связанные величины в реальной жизни.
Если одна величина увеличивается, а другая тоже растёт — это прямая пропорциональность. Если же одна растёт, а другая уменьшается — это обратная. Понимание этих зависимостей пригодится при решении задач о скоростях, работе, покупках и многом другом.

Основные определения
Прямо пропорциональные величины — это величины, которые изменяются в одну сторону: если одну умножить на число, вторая умножится на то же число.
Формула: y=kx , где k — коэффициент пропорциональности (постоянное число).
Обратно пропорциональные величины — это величины, которые изменяются в противоположные стороны: если одну умножить на число, вторая поделится на то же число.
Формула:
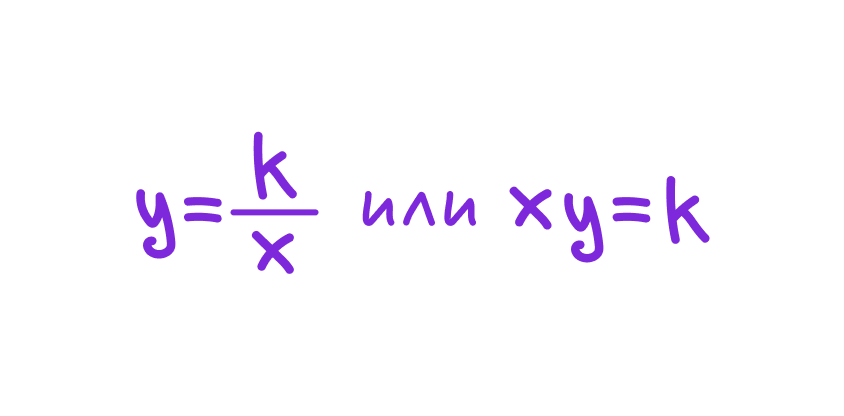
Признаки пропорциональности: если при изменении одной величины вторая изменяется пропорционально, то между ними пропорциональная зависимость.
Прямо пропорциональные величины
Прямо пропорциональные величины — это когда две вещи растут вместе или уменьшаются вместе, как лучшие друзья, которые всегда идут рука об руку.
Представим ситуацию из жизни: покупка конфет.
1 упаковка конфет стоит 20 рублей,
2 упаковки стоят 40 рублей,
3 упаковки стоят 60 рублей.
Очевидна закономерность: чем больше упаковок, тем больше стоимость. Увеличиваем количество конфет → растёт общая стоимость. Это прямая пропорциональность!
🤔 Как отличить прямую пропорциональность?
Лёгкий способ:
1. Берём две пары значений;
2. Делим одно на другое в каждой паре;
3. Получается одинаковое число? → это прямая пропорциональность.
Конфеты:
60 рублей ÷ 3 упаковки = 20 руб/упаковка
40 рублей ÷ 2 упаковки = 20 руб/упаковка
Число одинаковое — 20, значит — прямая пропорциональность.
Пример 1. Маша печёт печенье. За 2 часа испекла 60 штук. Сколько печенья Маша испечёт за 5 часов?
Решение ⤵
1. Найдём коэффициент пропорциональности: k = 60 : 2 = 30,
2. За 5 часов: y = 30 × 5 = 150 (печений).
Ответ: 150 печений.
💡
К прямой пропорциональности также относятся: расстояние и время, при постоянной скорости; стоимость и количество товара.
Обратно пропорциональные величины
Представим ситуацию «качели»:
Обратно пропорциональные величины — это когда одна вещь растёт, а другая уменьшается, как на качелях: одна сторона вверх, другая — вниз.
Представим ситуацию: маляры красят забор.
3 маляра красят забор за 4 дня
6 маляров покрасят тот же забор за 2 дня
Закономерность: чем меньше маляров, тем больше дней.
🤔 Как отличить обратную пропорциональность?
Лёгкий способ:
1. Берём две пары значений;
2. Умножаем одно на другое в каждой паре.
Получается одинаковое число? → это обратная пропорциональность.
3 маляра × 4 дня = 12
6 маляров × 2 дня = 12
Число 12 всегда одинаковое — это и есть признак обратной пропорциональности.
Пример 2. 4 человека укладывают плитку за 5 дней. Сколько дней нужно 10 людям?
Решение ⤵
1. 4 человека × 5 дней = 20
2. 10 человек × ? дней = 20
3. ? = 20 ÷ 10 = 2 (дня)
Ответ: 2 дня.
💡
К обратно пропорциональным величинам так же относятся: скорость и время пути; количество конфет, купленных на определённую сумму денег и их цена.
📝 Упражнения для самопроверки
Задание 1. Автобус едет со скоростью 50 км/ч. Сколько километров он проедет за 3 часа?
Решение ⤵
Раскройте, чтобы увидеть…
Прямая пропорциональность.
1. Найдём коэффициент пропорциональности: 50 км : 1 час = 50.
2. За 3 часа: 50 × 3=150 (км).
Ответ: 150 км.
Задание 2. 4 человека собирают 20 ящиков за 5 дней. Сколько дней нужно 10 людям?
Решение ⤵
Раскройте, чтобы увидеть…
Обратная пропорциональность.
1. 4 человека × 5 дней = 20
2. 10 человек × ? дней = 20
3. ? = 20 : 10 = 2 (дня).
Ответ: 2 дня.
Прямая и обратная пропорциональные зависимости объясняют многие процессы в жизни. Главное — запомнить формулы:
y=kx и xy=k,
И по ним находить коэффициент из условия и проверять норму. Эти знания пригодятся в задачах на движение, работу, а также в экономике и даже физике.
Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы. Первый урок — бесплатный 💜
 0
0
 0
0
 1
1








Комментарии 0