
Таблица производных функций
В 10-11-х классах ученики знакомятся с одним из важнейших инструментов математического анализа — производной. Это понятие помогает описать скорость изменения различных процессов, таких как движение, рост или убывание величин. Производная особенно важна для решения задач на экзаменах, включая ЕГЭ, где требуется анализ функций и их поведения. Чтобы уверенно работать с производными, необходимо знать таблицу производных основных функций, а также правила их применения. В этой статье рассмотрим, что такое производная функции, зачем она нужна и научимся использовать её для решения задач.
Что такое производная функции и зачем она нужна
📎 Производная функции — это мера того, насколько быстро меняется значение функции при изменении её аргумента. Если говорить простыми словами, производная показывает «скорость роста» или «скорость убывания» функции в конкретной точке.
Производная определяется как предел отношения изменения функции (Δy) к изменению аргумента (Δx), когда Δx стремится к нулю:
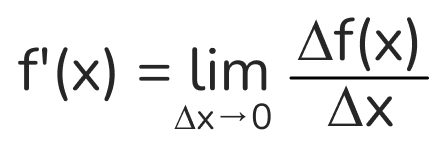
💡
Представьте, что вы наблюдаете за движением велосипедиста. Расстояние, которое он проехал, зависит от времени. Производная расстояния по времени — это скорость велосипедиста. Если скорость постоянна, то график расстояния будет прямой линией. Но если скорость меняется (например, велосипедист ускоряется или тормозит), то производная покажет, как именно происходит это изменение.
📌 Зачем нужна производная?
1. В физике: производная помогает описать законы движения: скорость (v(t)) — это производная пути (s(t)), а ускорение (a(t) ) — это производная скорости.
2. В экономике: производная используется для анализа роста доходов, расходов или прибыли. Например, если известна функция прибыли P(x), то её производная покажет, как меняется прибыль при увеличении объёма производства.
3. В биологии: производная может описывать скорость роста популяции, распространения болезней или изменения в экосистемах.
4. В геометрии: производная позволяет находить угловой коэффициент касательной к графику функции в заданной точке. Это важно для анализа поведения функции: где она возрастает, убывает или имеет экстремумы (максимумы и минимумы).
5. На практике: производная помогает решать задачи оптимизации. Например, как найти минимальные затраты на производство или максимальную прибыль.
💡
Допустим, ученик тренируется решать задачи по математике. В первый день он решает 5 задач, а каждый следующий день увеличивает количество решённых задач на 2. В первый день его результат можно описать как константу: y = 5, y′ = 0. Производная равна нулю, так как скорость изменения постоянна. Начиная со второго, дня количество задач начинает расти: y = 5 + 2x, y′ = 2. Здесь производная равна 2, что означает — количество решённых задач увеличивается на 2 задачи в день.
Производные основных элементарных функций
Для удобства вычисления производных существует таблица производных, которая охватывает основные элементарные функции. Давайте разберёмся, как выглядит эта таблица, и научимся использовать её на практике.

Эта таблица помогает быстро находить производные без необходимости выводить их каждый раз заново. Например, если нужно найти производную от 𝑥³, то из таблицы видно, что ответ будет — 3𝑥².
📌 Как пользоваться таблицей?
1. Определите тип функции
Сначала посмотрите, к какому типу относится ваша функция. Например, если у вас 𝑦 = sin 𝑥, то производная будет 𝑦′ = cos 𝑥.
2. Примените формулу из таблицы
Если функция сложная (например, 𝑦 = 3𝑥⁴), сначала найдите производную степени (4 · 𝑥³ = 4𝑥³), а затем умножьте её на коэффициент (3 · 4𝑥³ = 12𝑥³).
3. Сложные функции
Если функция состоит из нескольких частей (например, 𝑦 = sin(2𝑥)), используйте правило дифференцирования сложных функций.
Общие правила дифференцирования
Чтобы находить производные различных функций, нужно знать несколько базовых правил. Эти правила помогают упростить процесс вычисления, особенно если функция состоит из нескольких частей.
1. Вынесение константы за знак производной
Если функция умножается на число (константу), то это число можно вынести за знак производной:
(c ⋅ f)’ = c ⋅ f’
Пример:
Найдём производную функции y = 5x³.
Сначала выносим константу 5 за знак производной:
y’ = (5 ⋅ x³)’ = 5 ⋅ (x³)’
Находим производную x³ по таблице:
(x³)’ = 3x²
Подставляем результат:
y’ = 5 ⋅ 3x² = 15x²
2. Производная суммы или разности функций
Производная суммы (или разности) двух функций равна сумме (или разности) их производных:
(u + v)’ = u’ + v’, (u — v)’ = u’ — v’
Пример:
Найдём производную функции y = x² + sin(x).
Находим производные каждого слагаемого:
(x²)’ = 2x, (sin(x))’ = cos(x)
Складываем результаты:
y’ = 2x + cos(x)
3. Производная произведения функций
Для произведения двух функций используется следующая формула:
(u ⋅ v)’ = u’ ⋅ v + v’ ⋅ u
Пример:
Найдём производную функции y = x³ ⋅ cos(x).
Применяем формулу произведения:
y’ = (x³)’ ⋅ cos(x) + x³ ⋅ (cos(x))’
Находим производные:
(x³)’ = 3x², (cos(x))’ = -sin(x)
Подставляем результаты:
y’ = 3x² ⋅ cos(x) + x³ ⋅ (-sin(x)) = 3x² ⋅ cos(x) — x³ ⋅ sin(x)
4. Производная частного функций
Если функция представляет собой частное двух функций, то её производная вычисляется по формуле:
(u / v)’ = (u’ ⋅ v — v’ ⋅ u) / v², v ≠ 0
Пример:
Найдём производную функции y = x² / sin(x).
Применяем формулу частного:
y’ = ((x²)’ ⋅ sin(x) — x² ⋅ (sin(x))’) / sin²(x)
Находим производные:
(x²)’ = 2x, (sin(x))’ = cos(x)
Подставляем результаты:
y’ = (2x ⋅ sin(x) — x² ⋅ cos(x)) / sin²(x)
5. Производная сложной функции
Если функция является композицией двух функций, то её производная находится по правилу:
(f(g(x)))’ = f'(g(x)) ⋅ g'(x)
Пример:
Найдём производную функции y = sin(2x).
Здесь внешняя функция f(u) = sin(u), а внутренняя g(x) = 2x.
Находим производные:
f'(u) = cos(u), g'(x) = 2
Подставляем результаты:
y’ = cos(2x) ⋅ 2 = 2cos(2x)

Правила дифференцирования сложных функций
📎 Сложная функция — это функция, которая зависит от другой функции. Проще говоря, если одна функция «вложена» в другую, то такая конструкция называется сложной функцией. Чтобы найти её производную, нужно использовать специальное правило:
(f(g(x)))’ = f'(g(x)) ⋅ g'(x).
Это означает, что сначала находим производную внешней функции f, а затем умножаем её на производную внутренней функции g.
📌 Как это работает?
1. Определяем внешнюю и внутреннюю функции
Например, в выражении y = cos(3x + 5):
- Внешняя функция: cos(u), где u = 3x + 5.
- Внутренняя функция: u = 3x + 5.
2. Находим производные обеих функций:
- Производная внешней функции: (cos(u))’ = -sin(u).
- Производная внутренней функции: (3x + 5)’ = 3.
3. Умножаем результаты
y’ = -sin(u) ⋅ 3 = -sin(3x + 5) ⋅ 3 = -3sin(3x + 5).
Решение примеров
Пример 1
Найдём производную функции y = 4x³ — 2x² + 5x — 7.
1. Разделим функцию на слагаемые:
y = 4x³ — 2x² + 5x — 7.
2. Находим производные каждого слагаемого:
- (4x³)’ = 4 ⋅ 3x² = 12x².
- (-2x²)’ = -2 ⋅ 2x = -4x.
- (5x)’ = 5.
- (-7)’ = 0 (производная константы равна нулю).
3. Складываем результаты:
y’ = 12x² — 4x + 5.
Пример 2
Найдём производную функции y = (2x + 3)⁴.
1. Определим внешнюю и внутреннюю функции:
- Внешняя функция: u⁴, где u = 2x + 3.
- Внутренняя функция: u = 2x + 3.
2. Находим производные:
- Внешняя функция: (u⁴)’ = 4u³.
- Внутренняя функция: (2x + 3)’ = 2.
3. Умножаем результаты:
y’ = 4u³ ⋅ 2 = 8(2x + 3)³.
Пример 3
Найдём производную функции y = x² / sin(x).
1. Используем правило дифференцирования частного:
(u / v)’ = (u’ ⋅ v — v’ ⋅ u) / v², v ≠ 0.
2. Заменим u = x² и v = sin(x):
- u’ = (x²)’ = 2x.
- v’ = (sin(x))’ = cos(x).
3. Подставляем в формулу:
y’ = (2x ⋅ sin(x) — cos(x) ⋅ x²) / sin²(x).
Пример 4
Найдём производную функции y = e^(3x — 1).
1. Определим внешнюю и внутреннюю функции:
- Внешняя функция: e^u, где u = 3x — 1.
- Внутренняя функция: u = 3x — 1.
2. Находим производные:
- Внешняя функция: (e^u)’ = e^u.
- Внутренняя функция: (3x — 1)’ = 3.
3. Умножаем результаты:
y’ = e^u ⋅ 3 = 3e^(3x — 1).
Пример 5
Найдём производную функции y = ln(5x² + 2).
1. Определим внешнюю и внутреннюю функции:
- Внешняя функция: ln(u), где u = 5x² + 2.
- Внутренняя функция: u = 5x² + 2.
2. Находим производные:
- Внешняя функция: (ln(u))’ = 1/u.
- Внутренняя функция: (5x² + 2)’ = 10x.
3. Умножаем результаты:
y’ = 1/u ⋅ 10x = 10x / (5x² + 2).
В этой статье мы подробно разобрали ключевые понятия, связанные с функциями и их производными, а также изучили основные методы работы с ними.
Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы.
Первый урок по форме ниже — бесплатный ⤵
 9
9
 6
6
 8
8








Комментарии 0