Призма в геометрии: элементы, виды, свойства

В 10-м классе геометрия становится более сложной, и одной из важных тем является изучение многогранников. Среди них особое место занимает призма — это геометрическое тело, которое встречается как в учебных задачах, так и в реальной жизни. Призмы можно увидеть в архитектуре, технике и даже в природе.

В этой статье мы разберём, что такое призма, её основные элементы, виды, свойства и формулы. Также рассмотрим примеры призм в окружающем мире.

Что такое призма

📎 Призма — это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммы. Эти параллелограммы называются боковыми гранями , а равные многоугольники — основаниями призмы.

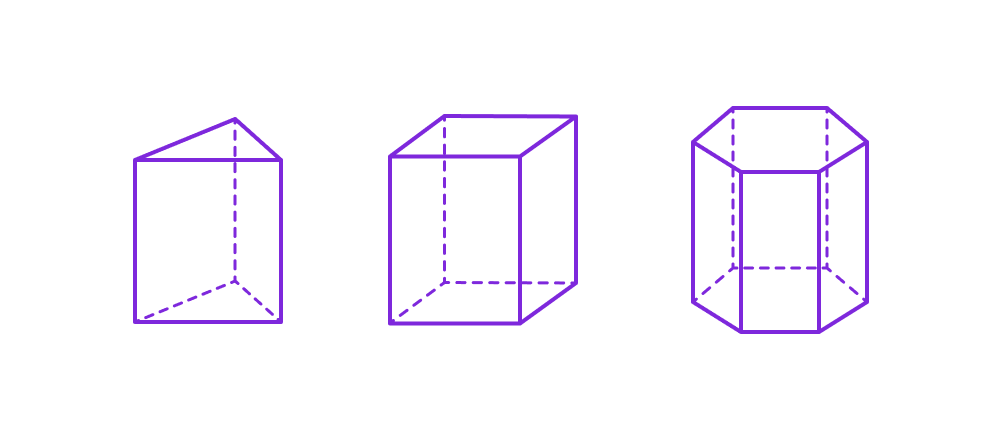
Пример: коробка или кирпич имеют форму призмы, где основания — прямоугольники, а боковые грани — тоже прямоугольники.

Основные элементы призмы

Призма состоит из следующих элементов ⤵︎

1. Основания
Два равных многоугольника, лежащих в параллельных плоскостях. Например, у треугольной призмы основания — треугольники, у шестиугольной призмы — шестиугольники.

2. Боковые грани
Параллелограммы, соединяющие соответствующие стороны оснований. У прямой призмы боковые грани — прямоугольники, а у наклонной — параллелограммы произвольной формы.

3. Боковая поверхность
Совокупность всех боковых граней призмы.

4. Полная поверхность
Объединение боковой поверхности и двух оснований.

5. Боковые рёбра
Отрезки, соединяющие вершины оснований. Все боковые рёбра призмы параллельны и равны между собой.

6. Высота
Перпендикуляр, проведённый между плоскостями оснований. Высота определяет расстояние между основаниями призмы.

7. Диагональ
Отрезки, соединяющие две вершины призмы, не принадлежащие одной грани. Например, диагональ может соединять вершину одного основания с вершиной другого.

8. Диагональная плоскость
Плоскость, проходящая через два боковых ребра призмы, не принадлежащие одной грани.

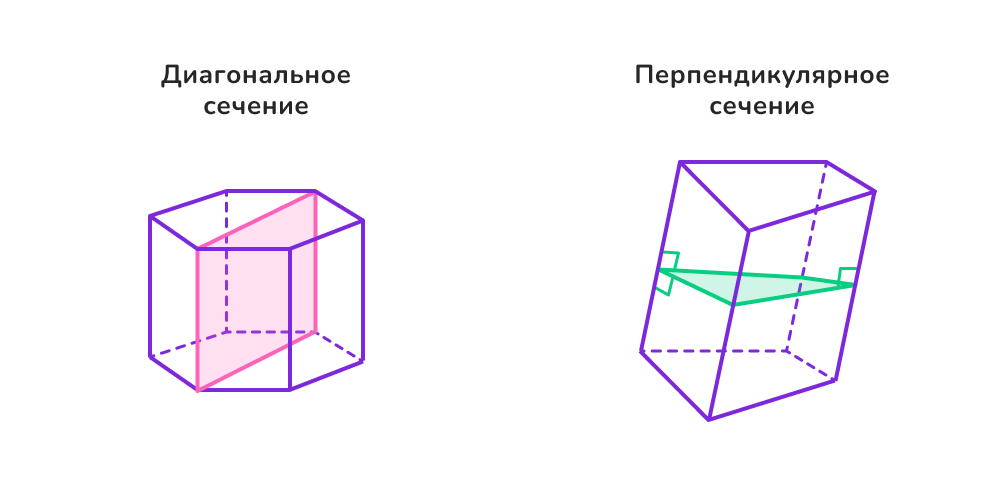
9. Диагональное сечение
Сечение призмы диагональной плоскостью. Оно представляет собой параллелограмм.

10. Перпендикулярное сечение
Сечение призмы плоскостью, перпендикулярной её боковым рёбрам. Это сечение позволяет вычислить площадь поперечного сечения призмы.

Виды призм и их свойства

1. Прямая призма

Прямая призма — это призма, у которой боковые рёбра перпендикулярны плоскостям оснований.

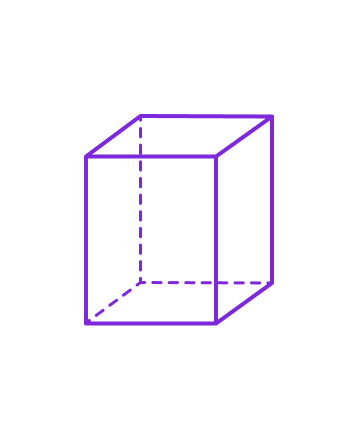
1. Боковые грани прямой призмы — прямоугольники.
2. Высота прямой призмы равна длине её бокового ребра.
3. Формула объёма:

2. Наклонная призмa

Наклонная призма — это призма, у которой боковые рёбра не перпендикулярны плоскостям оснований.

1. Боковые грани наклонной призмы — параллелограммы.
2. Высота наклонной призмы меньше длины её бокового ребра.
3. Формула объёма через площадь перпендикулярного сечения:

3. Правильная призма

Правильная призмa — это прямая призмa, основания которой являются правильными многоугольниками (все стороны и углы равны).

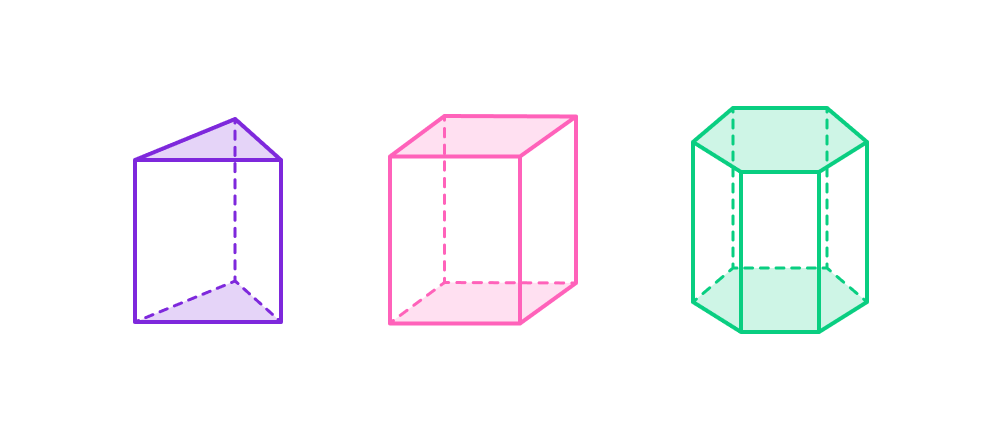
1. Все боковые грани правильной призмы — равные прямоугольники.
2. Углы между боковыми гранями и основаниями равны 90°.
3. Формула объёма через высоту (h), длину стороны (a) и количество сторон (n):

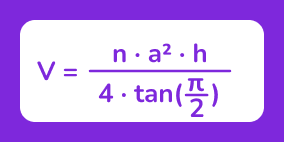
Формула площади полной поверхности:

4. Неправильная призма

Неправильная призмa — это призмa, основания которой являются неправильными многоугольниками.

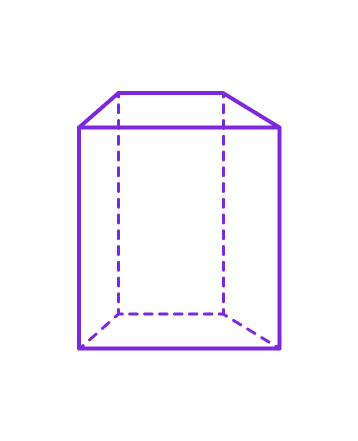
1. Боковые грани могут быть параллелограммами различной формы.
2. Формула объёма:

5. Усечённая призмa

Усечённая призмa — это часть призмы, отсекаемая плоскостью, не параллельной основаниям.

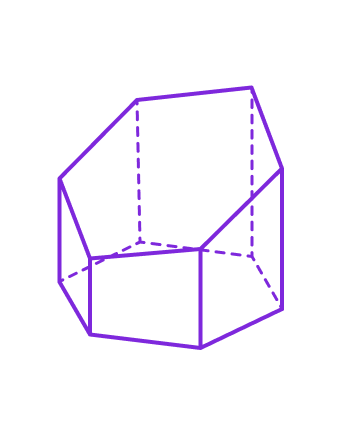
1. Призма усечённая имеет два основания разной формы.
2. Формула объёма:

Основные формулы

Рассмотрим дополнительные формулы для вычисления характеристик призмы ⤵︎

Призма вокруг нас

Призмы встречаются повсюду ⤵︎

1. Архитектура: здания часто имеют форму призм, например, небоскрёбы с прямоугольными или треугольными основаниями.
2. Техника: корпуса устройств, такие как холодильники или телевизоры, часто имеют форму призм.
3. Природа: кристаллы минералов, такие как кварц или алмаз, могут иметь форму призм.
4. Быт: коробки, книги и другие предметы домашнего обихода часто представляют собой призмы.

Мы разобрали, что такое призмa, её основные элементы, виды и свойства. Познакомились с формулами вычисления объёма, площади боковой и полной поверхности призмы. Также рассмотрели примеры призм в окружающем мире. Эти знания помогут вам лучше понять геометрию и применять её в решении задач и повседневной жизни.

Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к нашим репетиторам!