Приведение дробей к общему знаменателю

В этой статье мы разберём одну из самых важных тем в математике за 5-й класс — «Приведение дробей к общему знаменателю». Вы уже умеете сравнивать дроби с одинаковыми знаменателями. Например, понятно, что:

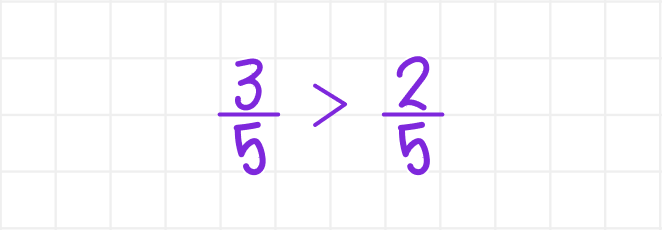
Следующий логичный вопрос: а как сравнить, сложить или вычесть дроби с разными знаменателями? Например, что больше:

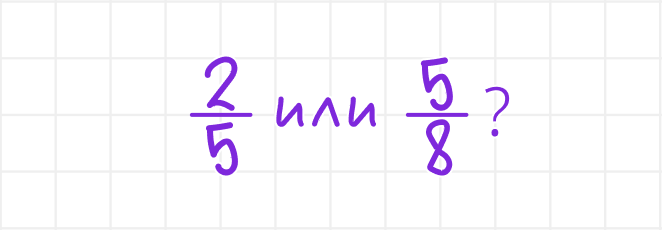
Для этого нам и нужно научиться делать так, чтобы знаменатели у дробей стали одинаковыми. Этот процесс и называется приведением к общему знаменателю.

Основные понятия

Давайте вспомним, из чего состоит дробь:

1. Числитель (верхняя часть) — показывает, сколько частей взяли.
2. Знаменатель (нижняя часть) — показывает, на сколько равных частей разделили целое.

Общий знаменатель — это число, которое будет общим (одинаковым) знаменателем для двух или более дробей. 

Самое главное правило, которое нельзя нарушать: если мы меняем знаменатель дроби, то мы должны точно так же изменить и её числитель, чтобы величина дроби не изменилась. 

Представьте, что у вас есть половина яблока ½. Если разрезать каждую половинку ещё пополам, то получится две четвертинки из четырёх — 2/4. А это всё та же половина яблока!

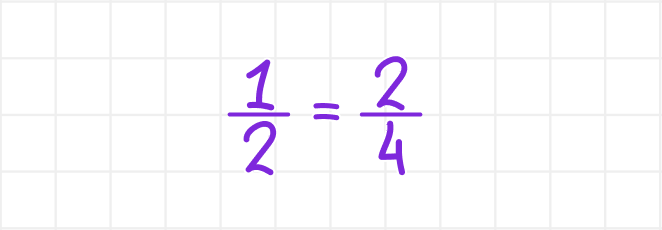
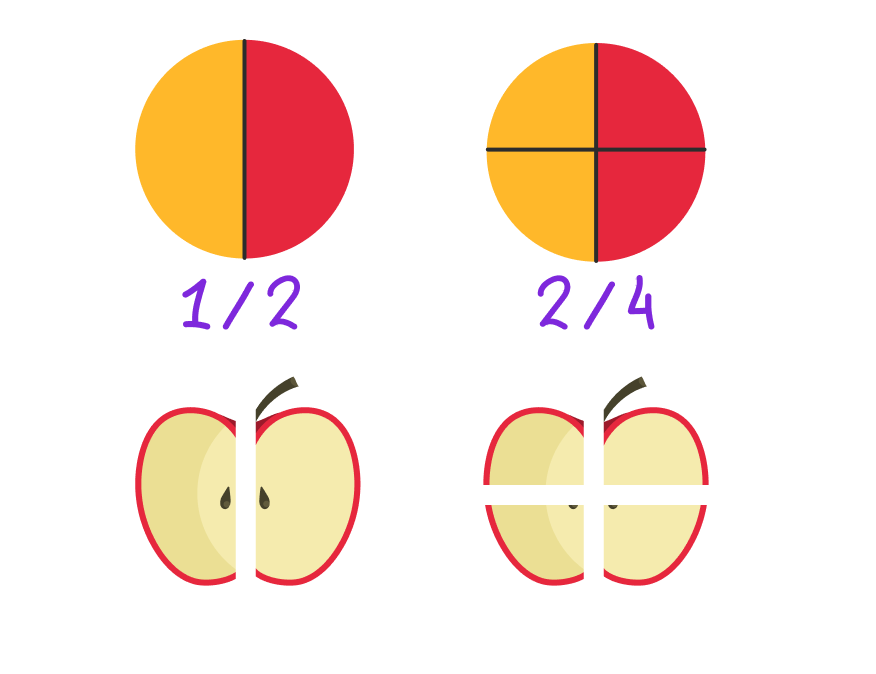
В примере с яблоком применено основное свойство дроби, которое нужно всегда помнить и знать, — оно помогает привести дроби к общему знаменателю.

Наименьший общий знаменатель (НОЗ) — это самый маленький из всех возможных общих знаменателей. С ним удобнее всего работать, так как числа получаются меньше.

Приведение дробей к общему знаменателю: алгоритм

Если нужно привести дроби к общему знаменателю, действуйте по шагам:

1️⃣ Найдите число, которое станет общим знаменателем. Лучше всего найти наименьшее общее кратное (НОК) знаменателей. Если НОК найти сложно, можно просто перемножить знаменатели — это всегда сработает, но числа могут получиться больше.

2️⃣ Для каждой дроби найдите дополнительный множитель. Для этого разделите новый общий знаменатель на старый знаменатель каждой дроби.

3️⃣ Умножьте числитель и знаменатель каждой дроби на свой дополнительный множитель. Помните наше золотое правило? Меняем и верх, и низ!

Примеры решения заданий

Рассмотрим несколько примеров, чтобы лучше понять тему.Пример 1. Приведите к общему знаменателю дроби.

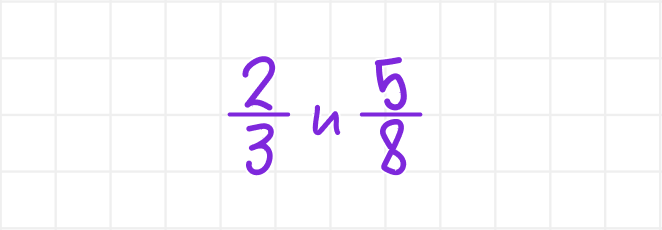
Решение: 

Шаг 1. Найдём общий знаменатель. Знаменатели 3 и 8. Наименьшее число, которое делится и на 3, и на 8 — это 24. Значит, НОЗ = 24.

Шаг 2. Найдём дополнительные множители.

1. Для дроби ⅔: 24 ÷ 3 = 8. Дополнительный множитель 8.
2. Для дроби ⅝: 24 ÷ 8 = 3. Дополнительный множитель 3.

Шаг 3. Умножаем каждую дробь на свой множитель.

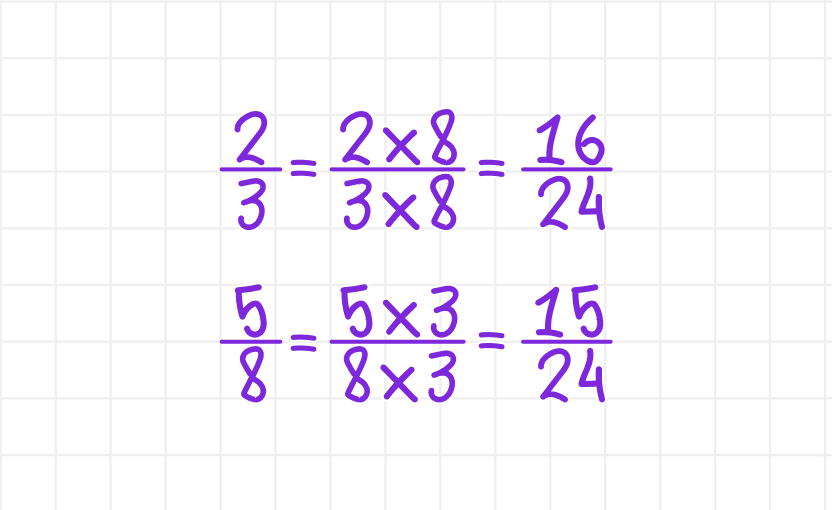
Готово! Теперь дроби

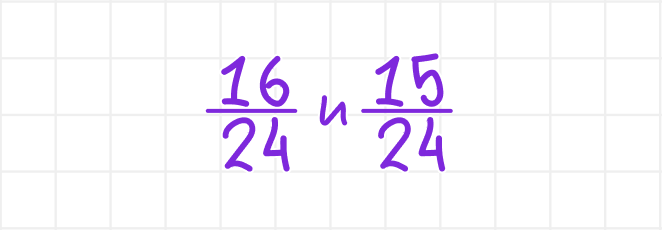
имеют общий знаменатель равный 24.

Пример 2. Приведите к общему знаменателю дроби.

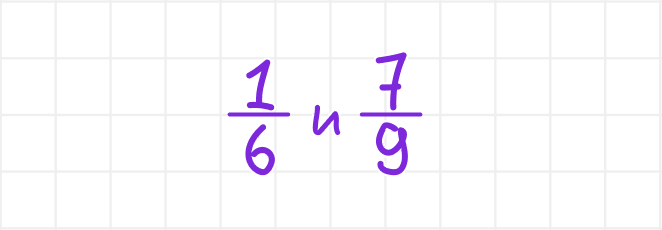
Решение:

Шаг 1. Ищем НОЗ для 6 и 9. Числа, кратные 6 — 6, 12, 18, 24… Кратные 9 — 9, 18, 27… НОК (6, 9) = 18. НОЗ = 18.

Шаг 2. Дополнительные множители.

1. Для ⅙: 18 ÷ 6 = 3.
2. Для 7/9: 18 ÷ 9 = 2.

Шаг 3. Умножаем:

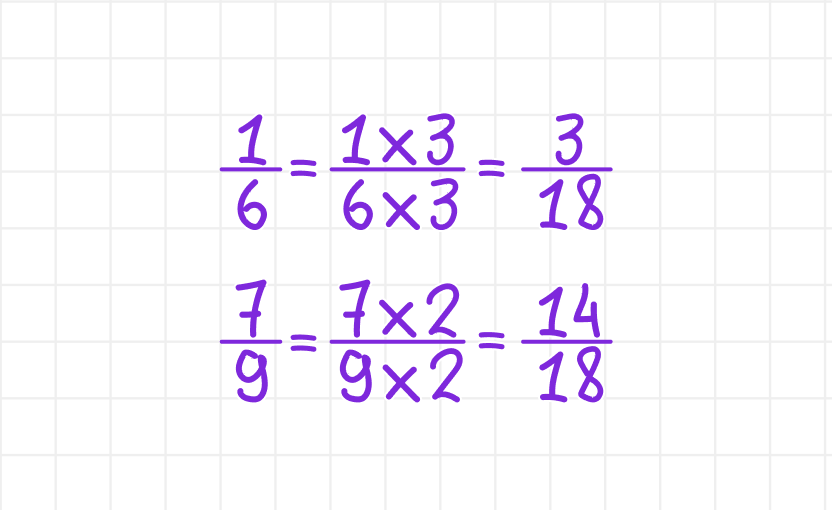
Задание выполнено, мы привели дроби ⅙ и 7/9 к общему знаменателю. Он равен 18.

📝 Упражнение для самопроверки

Упражнение 1. Приведите к наименьшему общему знаменателю дроби.

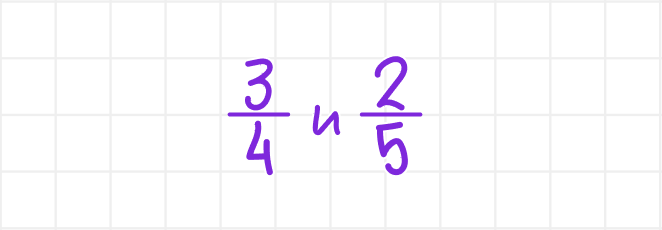
Решение:

Шаг 1. Найдём наименьший общий знаменатель (НОЗ) для чисел 4 и 5.
Так как 4 и 5 — взаимно простые числа (не имеют общих делителей, кроме 1), их наименьшее общее кратное равно их произведению: 4 × 5 = 20. Итак, НОЗ = 20.

Шаг 2. Найдём дополнительные множители для каждой дроби:

1. Для дроби ¾: 20 ÷ 4 = 5.
2. Для дроби ⅖: 20 ÷ 5 = 4.

Шаг 3. Приведём дроби к общему знаменателю 20, умножив числитель и знаменатель каждой дроби на её дополнительный множитель:

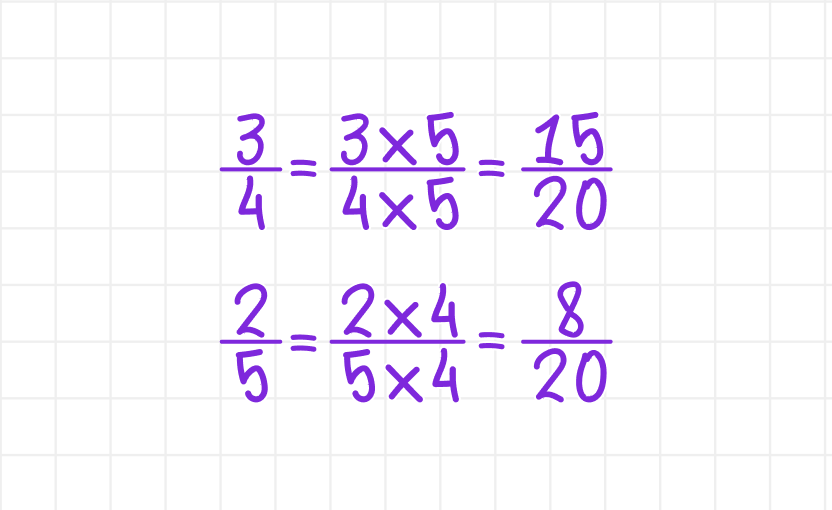
Ответ: Дроби ¾ и ⅖ при приведении к наименьшему общему знаменателю 20 имеют вид:

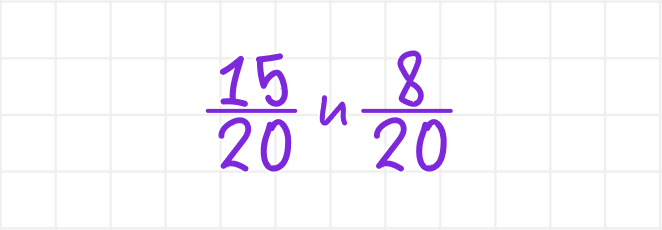
Сегодня мы узнали, что значит «привести дроби к общему знаменателю». Этот навык — настоящий ключик, который откроет вам двери к сложению и вычитанию любых дробей, а также к их сравнению. Главное — помните алгоритм и наше золотое правило: что делаем со знаменателем, то же самое делаем и с числителем. Тренируйтесь, и у вас всё получится!