Пирамида: определение, виды, формулы

Пирамида — это одна из самых интересных и важных фигур в геометрии, которая встречается не только в учебниках, но и в архитектуре, искусстве и даже природе. Изучение пирамид помогает лучше понять пространственные фигуры, их свойства и взаимосвязи с другими геометрическими телами. В 10-м классе ученики знакомятся с пирамидами, рассматривая их строение, виды, сечения и связь с другими телами, такими как сфера, конус и цилиндр.

В статье подробно рассматриваются основные аспекты пирамиды: её определение и состав, виды пирамид, взаимосвязь сферой, конусом и цилиндром, а также сечения пирамиды и необходимые формулы для решения задач.

Что такое пирамида и из чего она состоит 

Пирамида — это геометрическая фигура, которая представляет собой многогранник. Она состоит из основания и боковых граней, которые сходятся в одной точке, называемой вершиной пирамиды. Разберём подробнее, из чего состоит пирамида и как её элементы взаимодействуют между собой.

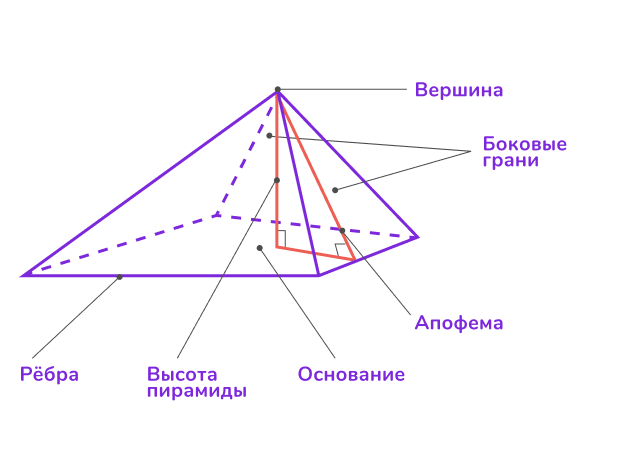
📎 Основание пирамиды

Основание пирамиды — это многоугольник, лежащий в плоскости. Оно может быть любого типа: треугольником, четырёхугольником (например, квадратом или прямоугольником), пятиугольником и так далее. Форма основания определяет название пирамиды. Например:

1. Если основание — треугольник, то пирамида называется треугольной.
2. Если основание — четырёхугольник, то пирамида называется четырёхугольной.
3. А если основание — правильный многоугольник (например, квадрат), то пирамида называется правильной.

Основание играет ключевую роль в определении свойств пирамиды. Например, если основание является правильным многоугольником, то пирамида обладает симметрией, а её высота проходит через центр основания.

📎 Боковые грани пирамиды

Боковые грани пирамиды — это треугольники, которые соединяют вершину пирамиды с рёбрами основания. Количество боковых граней равно количеству сторон основания. Например:

1. В треугольной пирамиде три боковые грани.
2. B четырёхугольной пирамиде четыре боковые грани.

Если пирамида правильная, то все её боковые грани являются равнобедренными треугольниками. Это важное свойство используется при решении задач на площадь поверхности и объём пирамиды.

📎 Вершина пирамиды

Вершина пирамиды — это единственная точка, которая не принадлежит плоскости основания. Именно в этой точке сходятся все боковые рёбра пирамиды. Вершина пирамиды определяет её высоту и положение относительно основания.

📎 Высота пирамиды

Высота пирамиды — это перпендикуляр, проведённый из вершины пирамиды к плоскости её основания. Высота является ключевым элементом для вычисления объёма пирамиды.

1. В правильной пирамиде высота проходит через центр основания (точку пересечения диагоналей, если основание — прямоугольник, или центр окружности, описанной вокруг правильного многоугольника).
2. В наклонной пирамиде высота не обязательно проходит через центр основания.

📎 Апофема пирамиды

Апофема — это высота боковой грани правильной пирамиды, проведённая из вершины пирамиды к стороне основания. Апофема используется для вычисления площади боковой поверхности пирамиды.

Например, если пирамида правильная, то длина апофемы одинакова для всех боковых граней. Это позволяет упростить вычисления.

📎 Рёбра пирамиды

Рёбра пирамиды — это отрезки, соединяющие вершину пирамиды с вершинами основания. Рёбра можно разделить на два типа:

1. Боковые рёбра — соединяют вершину пирамиды с вершинами основания.
2. Рёбра основания — стороны многоугольника, лежащего в основании.

Длина рёбер может быть разной в зависимости от формы пирамиды. Например, в правильной пирамиде все боковые рёбра равны.

📎 Диагонали основания

Как уже упоминалось, пирамида сама по себе не имеет противоположных вершин, но её основание может иметь диагонали, если оно является многоугольником с более чем тремя сторонами. Например:

1. В четырёхугольной пирамиде основание (четырёхугольник) имеет две диагонали.
2. B шестиугольной пирамиде основание (шестиугольник) имеет девять диагоналей.

Диагонали основания могут использоваться для анализа симметрии пирамиды, вычисления высоты или площади основания. Например, в правильной четырёхугольной пирамиде диагонали основания пересекаются в центре и делятся пополам.

Какими бывают пирамиды

Пирамиды можно классифицировать по различным признакам: форме основания, расположению вершины и свойствам граней. Рассмотрим основные виды пирамид.

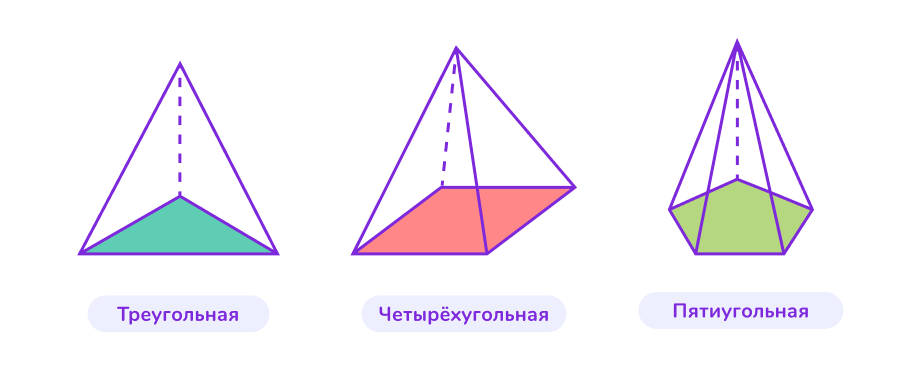
👉 По форме основания

Форма основания определяет название пирамиды и влияет на её свойства.

— Треугольная пирамида (тетраэдр)
Основание — треугольник. Это самая простая пирамида, состоящая из четырёх треугольных граней. Если все грани равносторонние треугольники, такая пирамида называется правильным тетраэдром.

— Четырёхугольная пирамида
Основание — четырёхугольник (например, квадрат или прямоугольник). В зависимости от формы основания, пирамида может быть правильной или неправильной.

— Шестиугольная пирамида
Основание — шестиугольник. Такая пирамида имеет шесть боковых граней.

— n-угольная пирамида
Основание — многоугольник с n сторонами. Число боковых граней равно числу сторон основания.

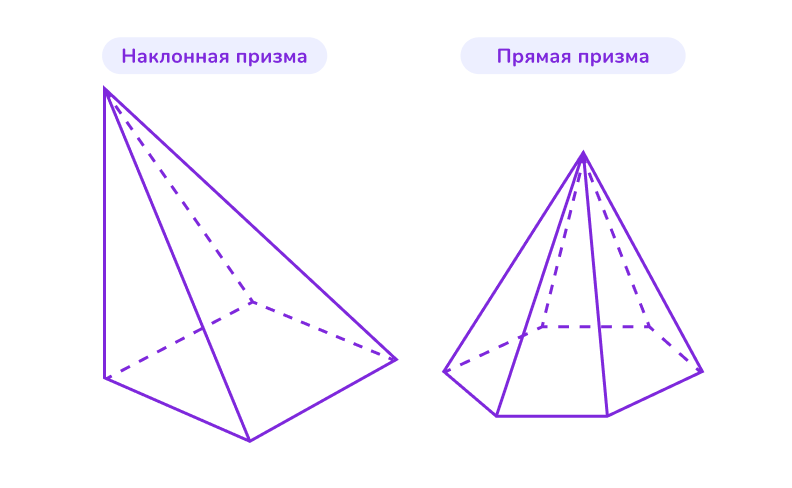
👉 По расположению вершины

Расположение вершины относительно основания также определяет тип пирамиды.

— Прямая пирамида
Вершина проецируется в центр основания, то есть высота пирамиды пересекает центр основания.

— Наклонная пирамида
Вершина не проецируется в центр основания, высота не совпадает с центральной осью.

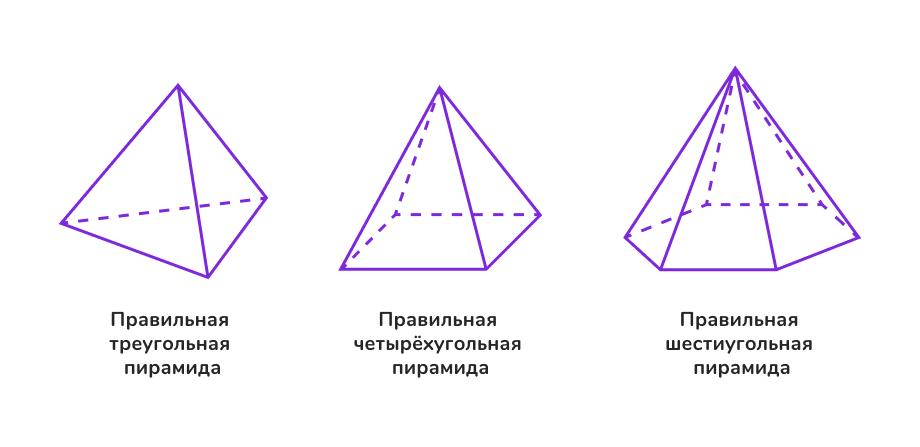
👉 По свойствам основания и граней

Свойства основания и боковых граней позволяют выделить особые виды пирамид.

— Правильная пирамида

1. Основание — правильный многоугольник (все стороны и углы равны).
2. Все боковые грани — равнобедренные треугольники.
3. Высота проходит через центр основания

— Неправильная пирамида
Основание или боковые грани не обладают указанными выше свойствами. Например, основание может быть произвольным многоугольником, а боковые грани — разными треугольниками.

— Усечённая пирамида
Пирамида, у которой верхняя часть отсечена плоскостью, параллельной основанию. Основаниями усечённой пирамиды являются два подобных многоугольника.

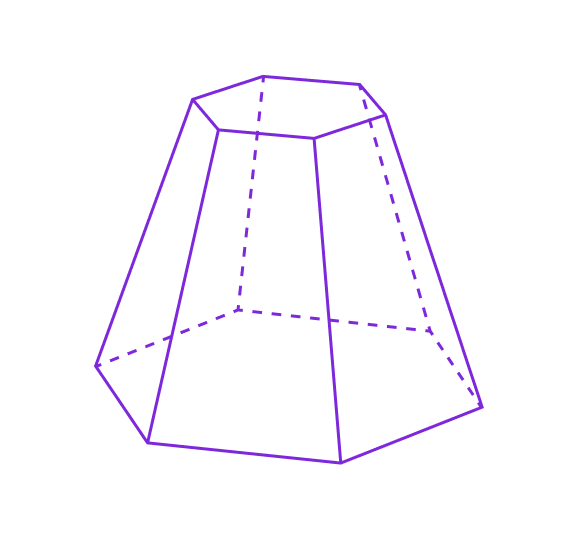
Пирамида и сфера

Они могут быть связаны двумя основными способами: вписанная сфера и описанная сфера. Рассмотрим каждый случай.

📌 Вписанная сфера

Определение: вписанная сфера — это сфера, которая касается всех граней пирамиды, включая основание.

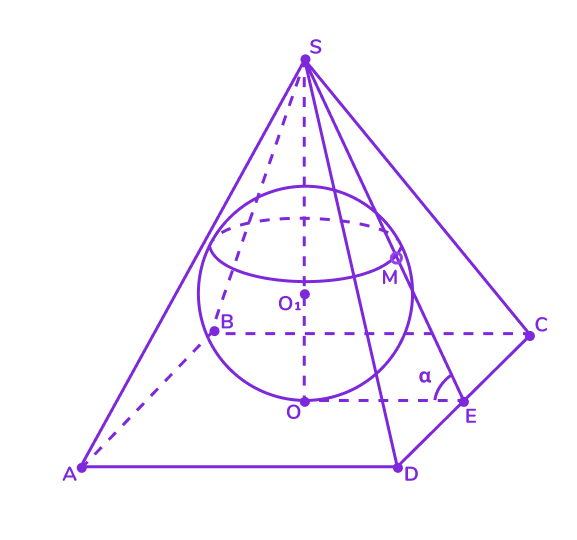
Условие существования:

1. Все грани пирамиды должны быть одинаково наклонены к основанию. Это условие выполняется для правильных пирамид, где боковые грани равны и симметричны.
2. Для треугольной пирамиды (тетраэдра) сфера может быть вписана всегда, если пирамида является правильной.

Центр сферы:

1. Центр вписанной сферы лежит на пересечении биссекторных плоскостей углов между гранями пирамиды.
2. В случае правильной пирамиды центр сферы также лежит на высоте пирамиды.

📌 Описанная сфера

Определение: описанная сфера — это сфера, которая проходит через все вершины пирамиды.

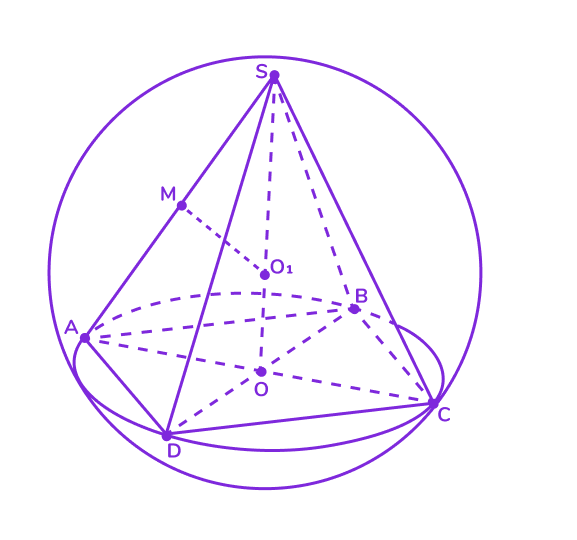
Условие существования:

1. Все вершины пирамиды должны лежать на одной сфере. Это всегда выполняется для треугольной пирамиды (тетраэдра), так как любые четыре точки в пространстве (не лежащие в одной плоскости) однозначно определяют сферу.
2. Для правильной пирамиды сфера описывается легко, так как её вершины равноудалены от центра основания.

Центр сферы:

1. Центр описанной сферы лежит на пересечении перпендикуляров, проведённых через центры окружностей, описанных вокруг основания и боковых граней.
2. В случае правильной пирамиды центр сферы также лежит на высоте пирамиды.

Пирамида и конус

Связь между пирамидой и конусом можно рассмотреть через условия вписывания одной фигуры в другую. Эти условия зависят от свойств пирамиды и конуса, а также их геометрических характеристик.

Пирaмида, вписанная в конус

Чтобы пирамиду можно было вписать в конус, должны выполняться следующие условия:

1. Все боковые рёбра пирамиды равны

1. Это означает, что пирамида является правильной.
2. Вокруг основания такой пирамиды можно описать окружность, причём центр этой окружности совпадает с центром основания пирамиды.

2. Перпендикуляр, опущенный из вершины пирамиды, проходит через центр её основания

1. Это одно из ключевых условий для вписывания пирамиды в конус.

3. Вершины конуса и пирамиды совпадают

1. То есть вершина пирамиды должна находиться в той же точке, что и вершина конуса.

Если все эти условия выполнены, то пирамида может быть вписана в конус.

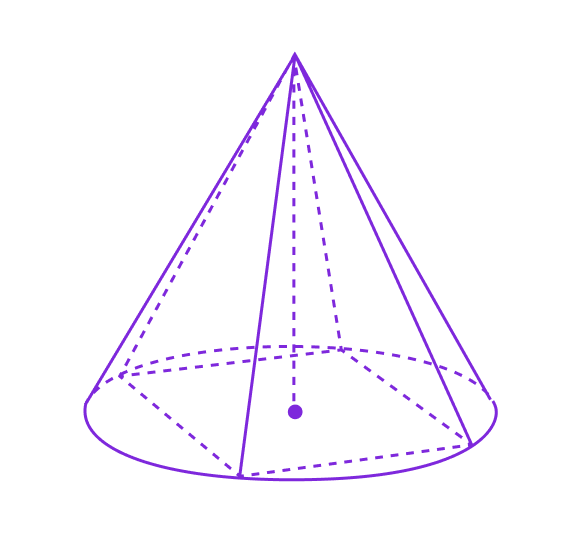
Конус, вписанный в пирамиду

Для того чтобы конус можно было вписать в пирамиду, необходимо соблюдение следующих условий:

1. Вершины конуса и пирамиды совпадают

1. Это основное требование для вписывания конуса.

2. Основание конуса вписано в основание пирамиды

1. Это означает, что окружность основания конуса касается всех сторон многоугольника, лежащего в основании пирамиды.

3. Апофемы пирамиды равны между собой

1. Равенство апофем обеспечивает симметричность пирамиды, что позволяет вписать в неё конус.

Если все три условия выполнены, то конус можно вписать в пирамиду.

Сечения пирамиды

Сечения пирамиды — это плоские фигуры, которые образуются при пересечении пирамиды плоскостью. В зависимости от положения секущей плоскости, сечения могут принимать разные формы. Рассмотрим основные случаи.

1. Сечение, параллельное основанию

1. Если секущая плоскость параллельна основанию пирамиды, то сечение будет подобно многоугольнику, лежащему в основании.
2. Например, если основание пирамиды — треугольник, то сечение также будет треугольником, подобным основанию.

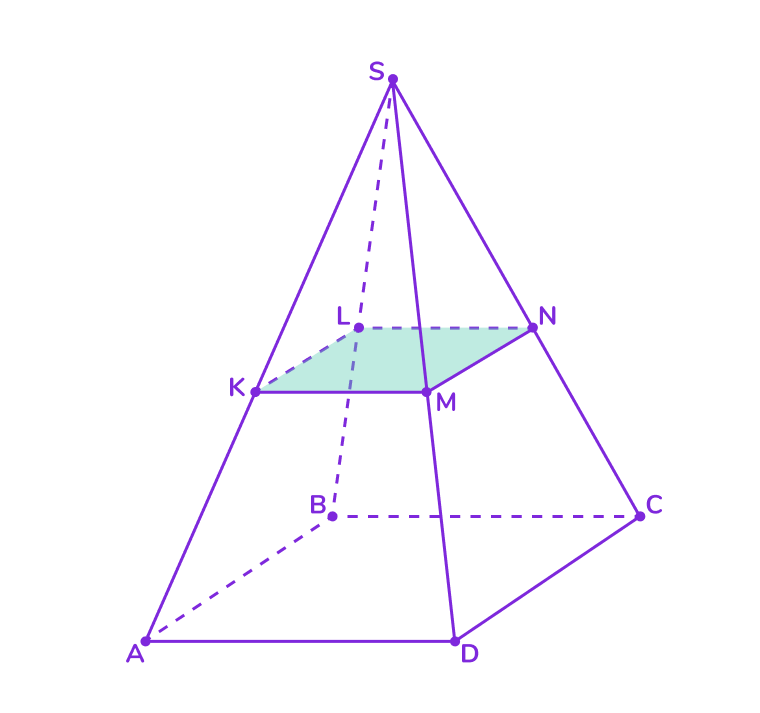
2. Сечение, проходящее через вершину и высоту

1. Если секущая плоскость проходит через вершину пирамиды и её высоту, то сечение будет треугольником.
2. В случае правильной пирамиды этот треугольник будет равнобедренным, а для правильного тетраэдра — равносторонним.

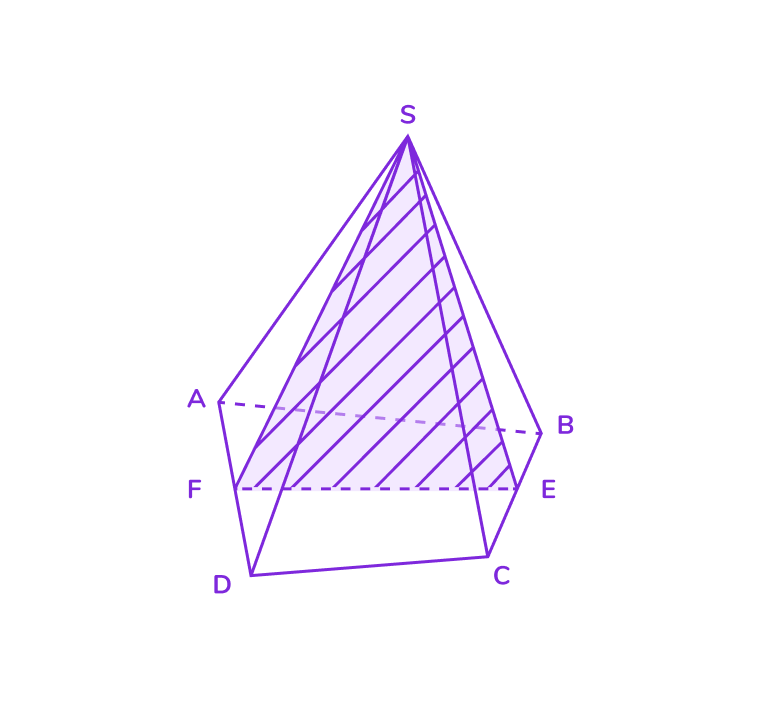
3. Диагональное сечение

1. Диагональное сечение — это сечение, которое проходит через вершину пирамиды и диагональ её основания.
2. Такое сечение всегда представляет собой треугольник.
3. Например, если основание пирамиды — четырёхугольник, то диагональное сечение будет треугольником, ограниченным двумя рёбрами пирамиды и одной из диагоналей основания.

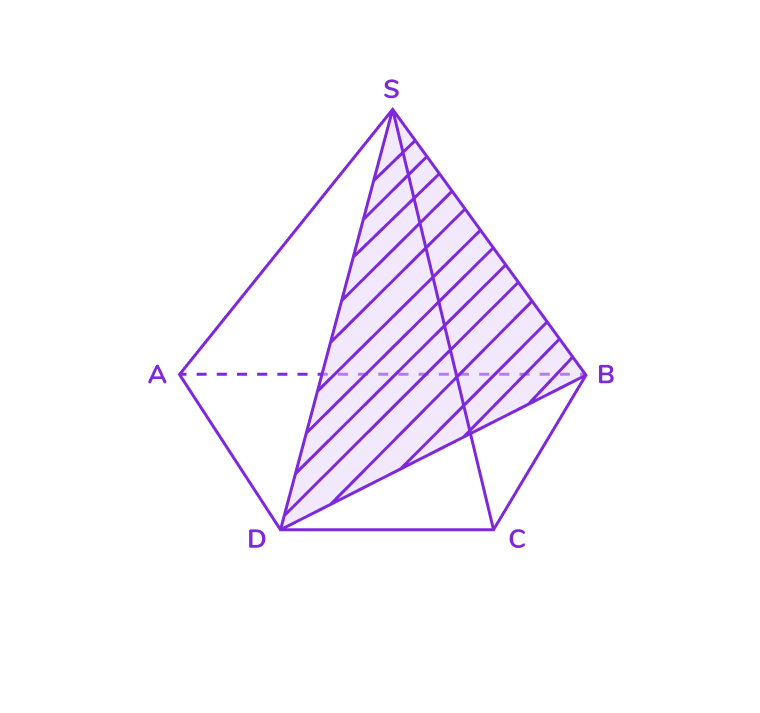
4. Сечение, проходящее через боковую грань и основание

1. Если секущая плоскость проходит через одну из боковых граней пирамиды и основание, то сечение будет трапецией.
2. В случае правильной пирамиды эта трапеция будет равнобедренной.

Памятка с формулами

Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы!