Параллельность прямых

Сегодня мы начинаем изучение одной из самых увлекательных тем в геометрии — параллельность прямых. Это понятие является краеугольным камнем всей геометрической науки и находит отражение в окружающем нас мире: от архитектурных сооружений до природных явлений.

Интересно, что понятие параллельности прямых стало основой для создания разных геометрических систем. В Евклидовой геометрии (название произошло от имени древнегреческого математика, жившего в 3 веке до н. э., положившего основу современной геометрии), которую мы изучаем в школе, через точку, не лежащую на прямой, можно провести только одну прямую, параллельную данной. Однако русский математик Николай Лобачевский создал неевклидову геометрию, где через точку вне прямой можно провести бесконечно много прямых, параллельных данной.

Важно: в школьном курсе мы работаем исключительно с евклидовой геометрией.

Практическая значимость темы параллельности прямых довольно широка:

1. Строительство и архитектура (параллельные стены, колонны).
2. Дизайн и искусство (композиция рисунков).
3. Техника (параллельные механизмы).
4. Природа (ряды растений в саду).
5. И много другое.

Определение параллельных прямых

Две прямые на плоскости называются параллельными, если они не пересекаются.

Обозначение: a∥b — читаем «а параллельна b».

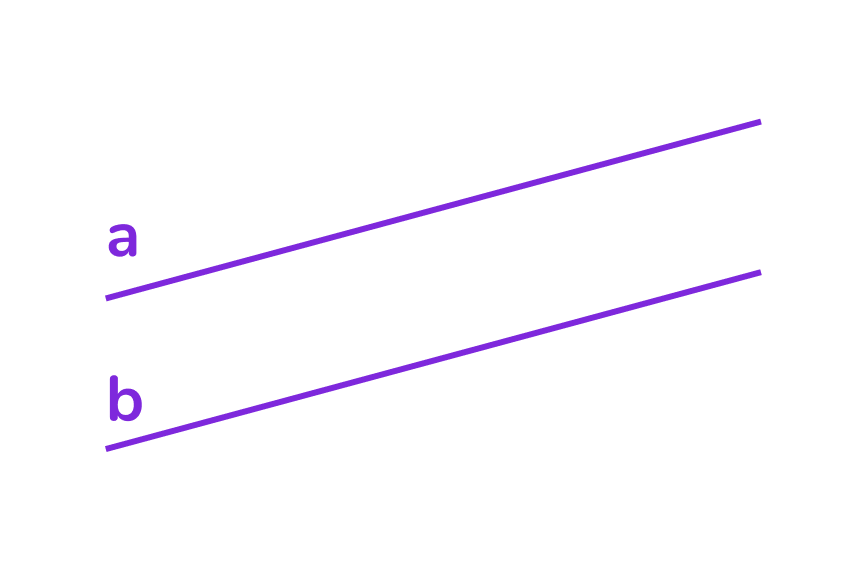
Параллельность часто можно встретить в окружающем мире. Например, представьте себе железнодорожные рельсы — они являются классическим примером параллельных прямых. 

Важные уточнения:

1. Параллельные прямые лежат в одной плоскости.

2. Они не имеют общих точек.

3. Расстояние между параллельными прямыми постоянно в любой точке.

Построим две параллельные прямые a и b,  проведём третью прямую с, пересекающую параллельные прямые, — она будет называться секущей (Рисунок 2). 

В результате построения у нас образуется 8 углов. Пары получившихся углов имеют свои названия: соответственные, односторонние и накрест лежащие.

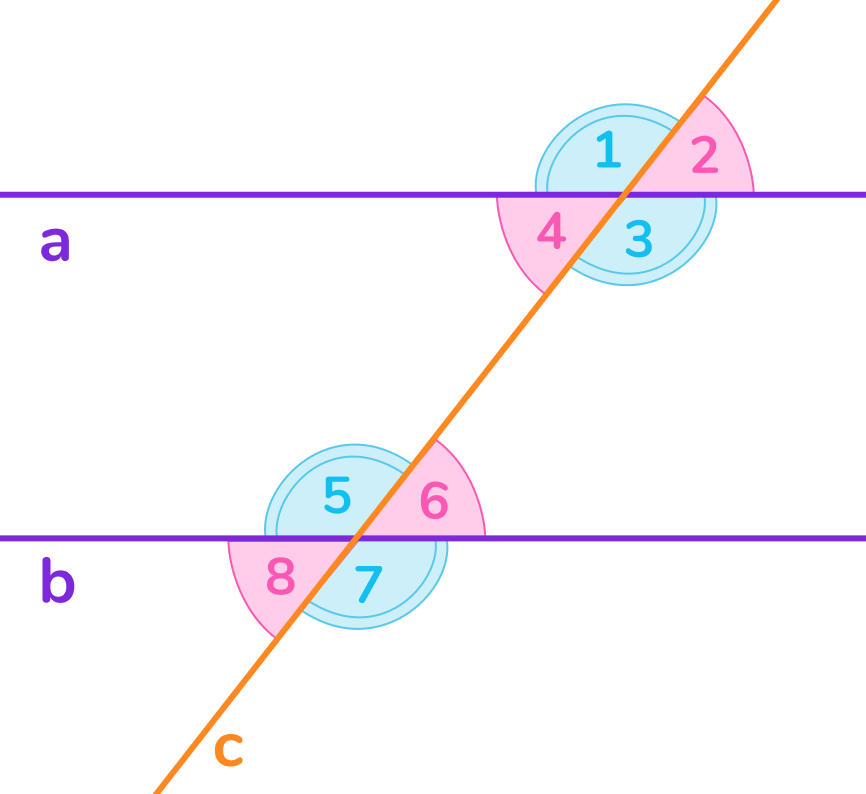
1. на рисунке a∥b, с — секущая;
∠1 и ∠5, ∠2 и ∠6, ∠3 и ∠7, ∠4 и ∠8 — соответственные; ∠3 и ∠5, ∠4 и ∠6 — накрест лежащие; ∠4 и ∠5, ∠3 и ∠6 — односторонние.

Свойства параллельных прямых

Рассмотрим свойства параллельных прямых.

Свойство 1

Если две прямые параллельны третьей прямой, то они параллельны между собой. 

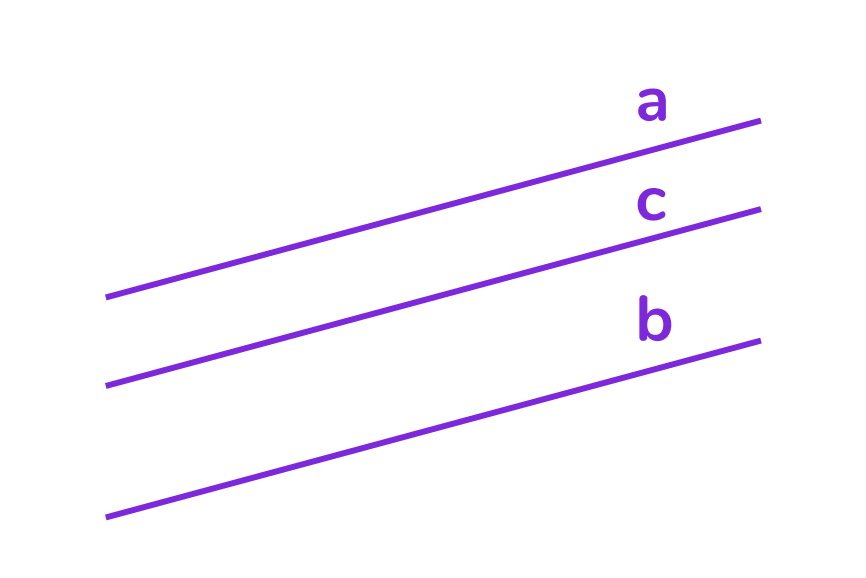
Если  a∥c и b∥c, то a∥b.

Свойство 2

Углы при параллельных прямых

Если две параллельные прямые пересечены третьей прямой (секущей), то:

1. Соответственные углы равны.
2. Накрест лежащие углы равны.
3. Сумма односторонних углов равна 180°.

Рассмотрим это свойство на примере некоторых пар углов, изображённых на рисунке 2:

1. ∠1 = ∠5 (соответственные);
2. ∠3 = ∠5 (накрест лежащие);
3. ∠4 + ∠5 = 180° (односторонние)

Признаки параллельности прямых

Признак 1

По равенству соответственных углов

Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.

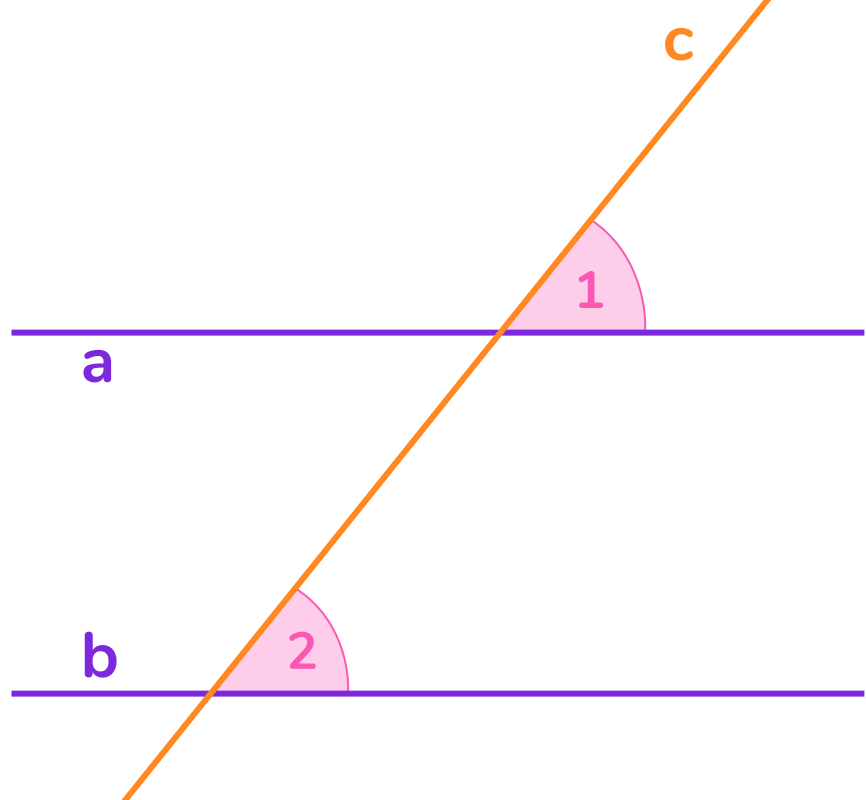
Если a∩c, b∩c, ∠1 = ∠2, то a∥b.

Интересно, что при строительстве домов рабочие проверяют параллельность стен, измеряя соответственные углы.

Признак 2

По равенству накрест лежащих углов

Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.

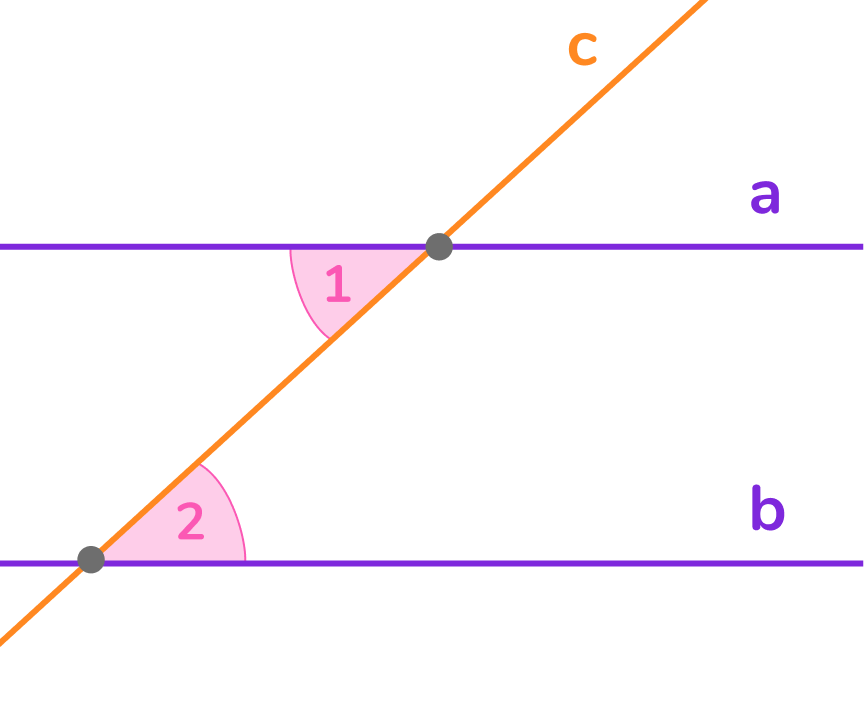
Если a∩c, b∩c, ∠1 = ∠2, то a∥b.

Интересно, что в дизайне паркового ландшафта этим признаком проверяют параллельность дорожек.

Признак 3

По сумме односторонних углов

Если при пересечении двух прямых третьей сумма односторонних углов равна 180°, то прямые параллельны.

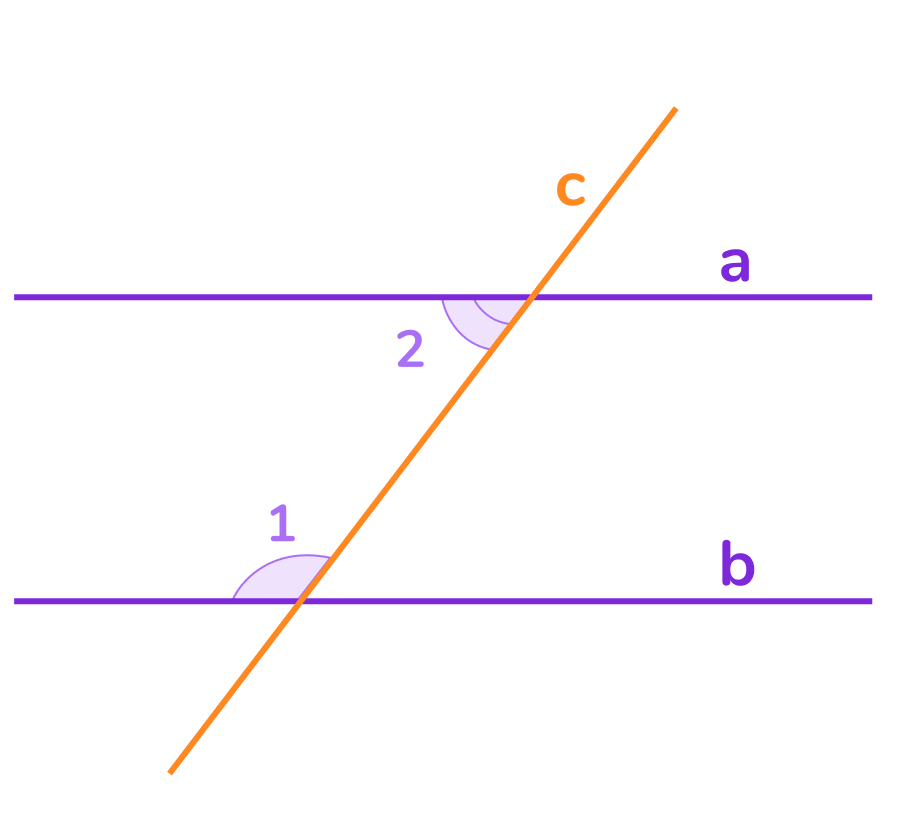
Если a∩c, b∩c, ∠1 + ∠2 = 180⁰, то a∥b.

Интересно, что при создании чертежей инженеры используют этот признак для проверки параллельности линий.

Признак 4

По перпендикулярности к третьей прямой

Если две прямые перпендикулярны третьей прямой, то они параллельны между собой.

Например, вертикальные столбы забора, все перпендикулярные земле, параллельны друг другу.

Параллельность прямых: примеры решения задач

Задача 1.

Даны две прямые a и b, и секущая c. Известно, что ∠1 = 65°, ∠2 = 115°. Докажите, что a∥b.

Решение:

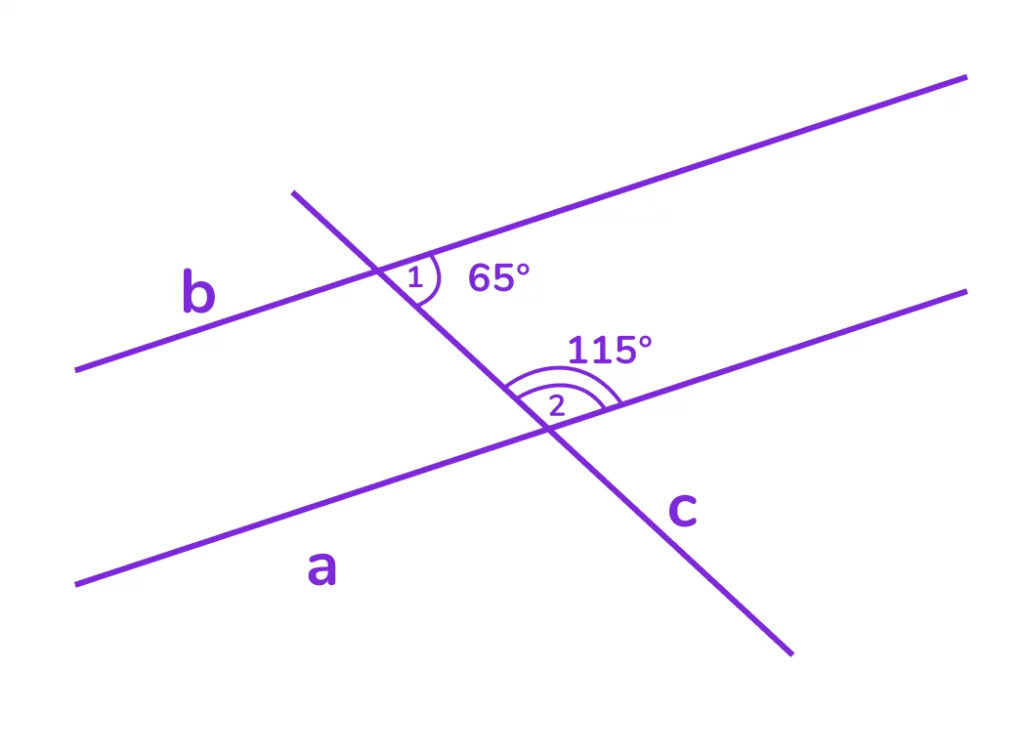
1. ∠1 и ∠2 — односторонние углы.
2. ∠1 + ∠2 = 65° + 115° = 180°.
3. По признаку параллельности (сумма односторонних углов равна 180°) делаем вывод, что a∥b.
4. Доказано.

Задача 2.

Даны две прямые a и b, причем a∥b и с — секущая. ∠1 = 70°. Найдите все остальные углы.

Решение:

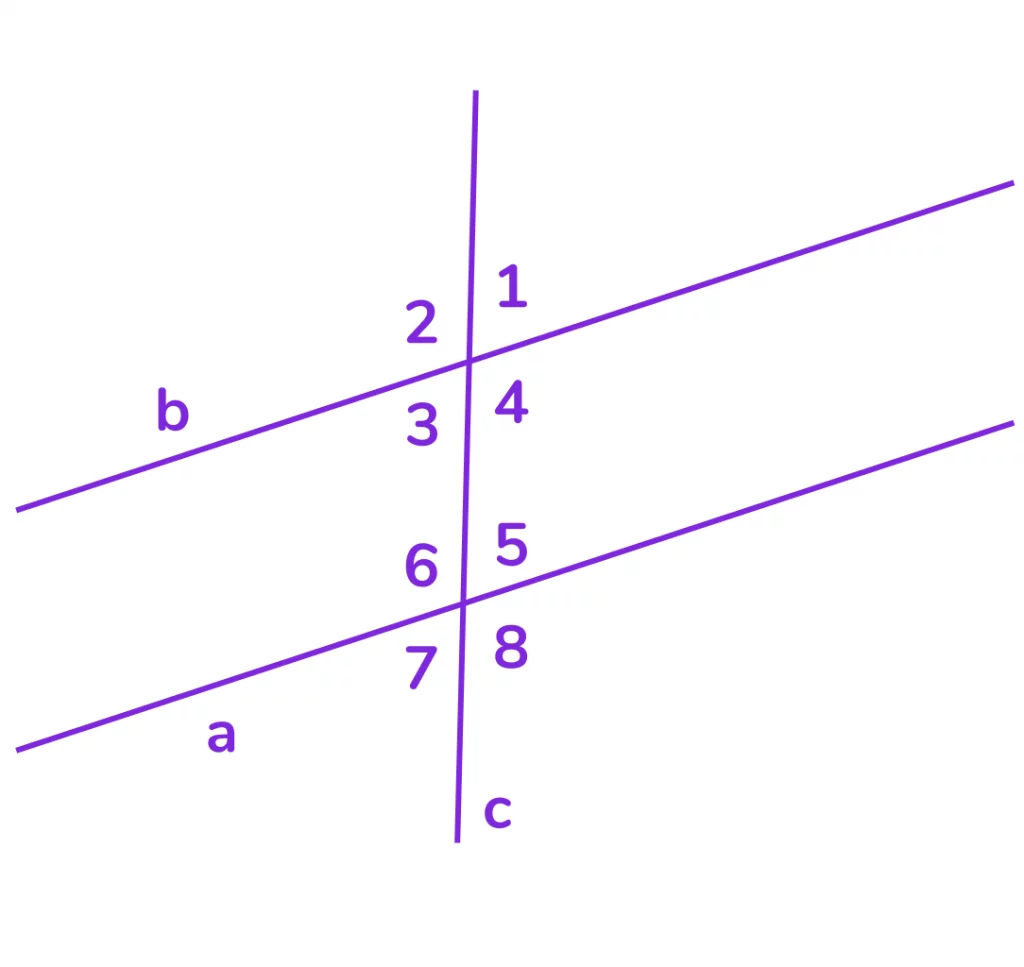
1. ∠3 = ∠1 = 70° (вертикальные);
2. ∠5 = ∠1 = 70° (соответственные);
3. ∠7 = ∠5 = 70° (вертикальные);
4. ∠2 = 180° — ∠1 = 110° (смежные);
5. ∠4 = ∠2 = 110° (вертикальные);
6. ∠6 = ∠4 = 110° (накрест лежащие);
7. ∠8 = ∠6 = 110° (вертикальные).

Ответ: 70°, 110°, 70°, 110°, 70°, 110°, 70°, 110°

📝 Упражнения для самопроверки

Дано: ∠1 = 120°, ∠2 = 60°. Определите, параллельны ли прямые, если эти углы:
а) соответственные;
б) накрест лежащие;
в) односторонние.

Решение:

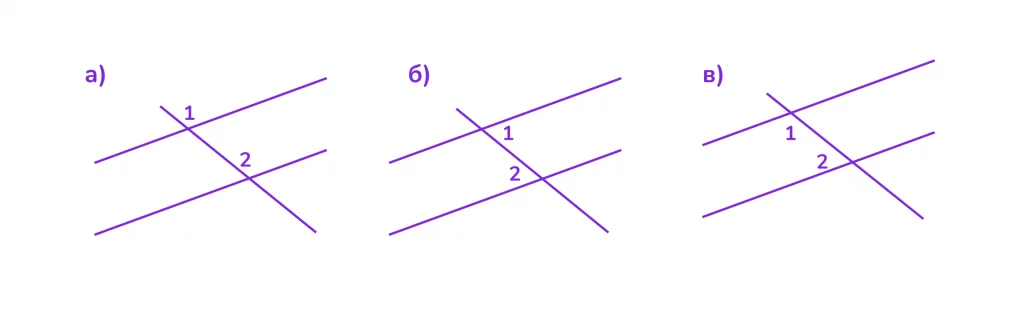
а) соответственные углы не равны ( 120° ≠ 60°), значит прямые не параллельны (не подходит под условие признака параллельности прямых);

б) накрест лежащие углы не равны ( 120° ≠ 60°), значит прямые не параллельны (не подходит под условие признака параллельности прямых);

в) односторонние углы в сумме дают 180° (120° + 60° =180°), значит по признаку параллельности прямых, прямые параллельны.  

Ответ: а) не параллельны; б) не параллельны; в) параллельны.

Мы изучили тему «Параллельность прямых» — одну из фундаментальных тем геометрии. Теперь вы можете не только решать геометрические задачи, но и видеть проявления математических закономерностей в окружающем мире.

Выделим важные итоги:

1. Параллельные прямые не пересекаются и лежат в одной плоскости.
2. Существуют признаки и свойства параллельных прямых.
3. Знание этой темы поможет в изучении последующих разделов геометрии.
4. Полученные навыки пригодятся в практической деятельности.

Советы для успешного обучения:

1. Всегда делайте аккуратные чертежи.

2. Внимательно изучайте условие задачи.

3. Тренируйтесь в доказательствах.

4. Связывайте теоретические знания с практикой.

Развивайте свой интерес к геометрии, обращая внимание на геометрические формы в архитектуре, природе, технике. Помните: математика — это не просто школьный предмет, а язык, на котором говорит вся Вселенная.