Основное тригонометрическое тождество

В курсе геометрии вы уже знакомились с основным тригонометрическим тождеством sin²α + cos²α = 1, рассматривая его в контексте прямоугольных треугольников. Однако в алгебре это тождество раскрывается с новой стороны — как фундаментальное соотношение, позволяющее преобразовывать сложные тригонометрические выражения и доказывать другие тождества.

Основное тригонометрическое тождество имеет огромное значение в математике и её приложениях — от решения уравнений до анализа колебательных процессов в физике и технике. Понимание и уверенное владение этим тождеством необходимо для дальнейшего изучения тригонометрии и математического анализа.

Основное тригонометрическое тождество и его доказательство

Для любого угла α выполняется равенство: sin²α + cos²α = 1

Доказательство ⤵

Рассмотрим единичную окружность (окружность с центром в начале координат и радиусом, равным 1) в прямоугольной системе координат. Возьмём произвольный угол α, который образует радиус-вектор OM с положительным направлением оси Ox.

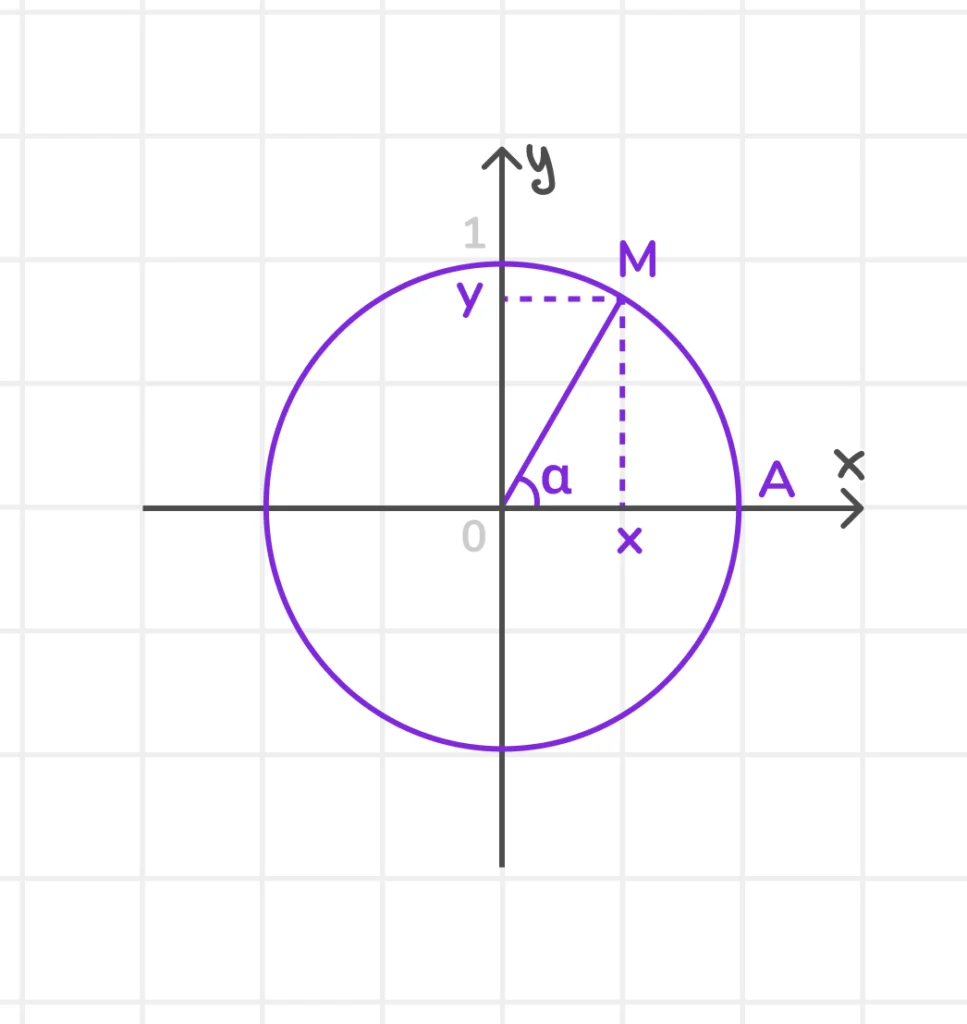
Координаты точки M на окружности:

1. x = cos α (т. к. cos α = х/1);
2. y = sin α (т. к. sin α = y/1).

Расстояние от точки M до начала координат вычисляется по формуле:

OM = √(x² + y²) = √(cos²α + sin²α)

Поскольку OM является радиусом единичной окружности, его длина равна 1:

√(cos²α + sin²α) = 1

Возводя обе части в квадрат, получаем:

cos²α + sin²α = 1

Что и требовалось доказать.

Следствия из основного тригонометрического тождества

Из основного тождества выводятся важные формулы ⤵

1️⃣ Выражение синуса через косинус и наоборот:

1. sinα = ±√(1 — cos²α);
2. cosα = ±√(1 — sin²α).

Знак выбирается в зависимости от координатной четверти, в которой находится угол α.

2️⃣ Связь с тангенсом и котангенсом:

1. если почленно разделить левую и правую части основного тригонометрического тождества на cos²α, то получим следующее тождество: 1 + tg²α = 1/cos²α;
2. если почленно разделить левую и правую части основного тригонометрического тождества на sin²α, то получим следующее тождество: 1 + ctg²α = 1/sin²α.

Эти формулы справедливы при α ≠ π/2 + πk для тангенса и α ≠ πk для котангенса.

Пример решения задачи

Задача. Найдите cosα, если sinα = 3/5 и α ∈ (π/2; π).

Решение ⤵

1. Используем основное тригонометрическое тождество:

sin²α + cos²α = 1.

2. Подставляем известное значение:

(3/5)² + cos²α = 1;
9/25 + cos²α = 1.

3. Выражаем cos²α:

cos²α = 1 — 9/25 = 16/25.

4. Извлекаем корень:

cosα = ±√(16/25) = ±4/5.

5. Выбираем знак: поскольку α ∈ (π/2; π) (вторая четверть), косинус отрицателен.

Ответ: cosα = -4/5.

📝 Упражнение для самопроверки

Упражнение. Найдите sinα, если cosα = -12/13 и α ∈ (π; 3π/2).

Решение ⤵

1. Применим основное тригонометрическое тождество:

sin²α + cos²α = 1.

2. Подставим известное значение:

sin²α + (−12/13)² = 1;
sin²α + 144/169 = 1.

3. Выразим sin²α:

sin²α = 1 — 144/169=25/169.

4. Найдём sinα:

sinα = ±√(25/169) = ±5/13.

5. Определим знак синуса по условию α ∈ (π;3π/2) — это третья четверть, где синус отрицателен, поэтому:

sinα = −5/13.

Ответ: -5/13.

Основное тригонометрическое тождество связывает синус и косинус одного угла и является ключевым инструментом для преобразования тригонометрических выражений. Его следствия позволяют выражать одни тригонометрические функции через другие, что особенно полезно при решении уравнений и упрощении сложных выражений. Регулярная практика в применении этого тождества поможет развить навыки, необходимые для успешного освоения курса тригонометрии.