Как правильно округлять числа

Округление чисел — это метод преобразования числа в более удобное для работы значение, которое проще использовать в расчётах или для представления в отчётах. Этот процесс особенно важен при работе с приближёнными значениями в науке, финансах и других областях, где требуется упрощение сложных чисел. В этой статье мы рассмотрим основные принципы округления чисел, которые изучаются в школе в 5–6-х классах.

Приближённые значения

Приближённые значения часто используются для упрощения чисел. Они могут быть как приближением вниз (с недостатком), так и приближением вверх (с избытком). Эти подходы позволяют сделать числа более удобными для работы, особенно когда требуется сделать расчёты менее громоздкими.

Округление чисел: приближённые значения с недостатком

Приближённые значения с недостатком используются, когда необходимо округлить число вниз, то есть уменьшить его значение. Это полезно для того, чтобы быть более консервативным в расчётах, или когда требуется уменьшить результат, чтобы избежать излишнего увеличения.

Округление чисел: практические примеры с недостатком

1. Округление цены товара:

Цена товара составляет 14,89 рубля. Для простоты расчётов округляем до 14 рублей.

2. Округление количества продуктов:

У вас есть 11,2 килограмма муки. Для удобства планирования и использования округляем до 11 килограммов.

3. Округление оценки в тесте:

Ученик набрал 89,7 баллов на экзамене. Учитель округляет результат до 89 баллов, чтобы быть строже в оценке.

Приближённые значения с избытком

Приближённые значения с избытком применяются, когда необходимо округлить число вверх, увеличив его значение. Это может быть важно для учета потенциальных дополнительных значений или при планировании.

1. Округление стоимости проезда:

Стоимость проезда на автобусе составляет 99,6 рублей. Чтобы не возиться с мелкими монетами, округляем до 100 рублей.

2. Округление числа участников:

Планируется мероприятие с 98,3 ожидаемыми участниками. Чтобы предусмотреть всех возможных гостей и избежать нехватки мест, округляем до 99 участников.

3. Округление объёма закупок:

Компания планирует закупить 13,7 тонн сырья. Чтобы обеспечить непрерывность производства и избежать остановок, округляем до 14 тонн.

Что значит округлить число

Округление натуральных чисел — это процесс приближения числа к ближайшему целому числу, которое является кратным заданной степени десяти (например, к ближайшей десятке, сотне и т. д.). Этот процесс помогает упростить числа для более легкого восприятия и работы с ними.

Правила округления

1. Округление до ближайшего целого числа:

Если цифра в разряде, следующем за округляемым, меньше 5, то цифра в округляемом разряде остаётся без изменений, а все следующие за ней цифры заменяются на нули.

Если цифра в разряде, следующем за округляемым, равна 5 или больше, то цифра в округляемом разряде увеличивается на 1, а все следующие за ней цифры заменяются на нули.

Алгоритм округления натуральных чисел

1. Определение разряда округления:

Определите, до какого разряда нужно округлить число (десятки, сотни, тысячи и т. д.).

2. Проверка следующей цифры:

Посмотрите на цифру, которая находится сразу после разряда округления.

3. Применение правила округления:

Если цифра после разряда округления меньше 5, округляемое число остаётся без изменений, а все следующие цифры заменяются на нули.

Если цифра после разряда округления равна 5 или больше, к округляемому числу прибавляется 1, а все следующие цифры заменяются на нули.

Округление чисел: примеры натуральных чисел

Пример 1. Округление до ближайшей десятки.

Число: 47

1. Округляем до десятков.
2. Следующая цифра: 7 (больше 5).
3. Округлённое число: 50.

Пример 2. Округление до ближайшей сотни.

Число: 163

1. Округляем до сотен.
2. Следующая цифра: 6 (больше 5).
3. Округлённое число: 200.

Округление десятичных дробей

Округление десятичных дробей требует учёта количества знаков после запятой. Это может быть полезно для упрощения расчётов или для представления данных в удобном формате.

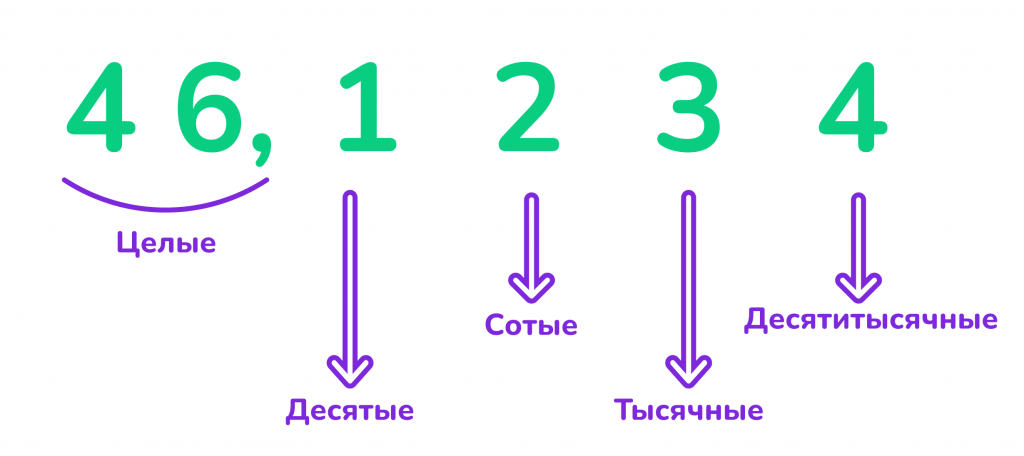
Алгоритм округления десятичных дробей

1. Определение разряда округления:

Определите, до какого разряда нужно округлить число (до десятых, сотых, тысячных и т. д.).

2. Проверка следующей цифры:

Посмотрите на цифру, которая находится сразу после разряда округления.

3. Применение правила округления:

Если цифра после разряда округления меньше 5, цифра в округляемом разряде остаётся без изменений.

Если цифра после разряда округления равна 5 или больше, цифра в округляемом разряде увеличивается на 1.

4. Отбрасывание лишних цифр:

Все цифры, находящиеся справа от округляемого разряда, отбрасываются.

Примеры округления десятичных дробей

Пример 1. Округление до ближайшей десятой доли.

Число: 4,73

1. Округляем до десятых.
2. Следующая цифра: 3 (меньше 5).
3. Округлённое число: 4,7.

Пример 2. Округление чисел до ближайшей сотой доли

Число: 9,856

1. Округляем до сотых.
2. Следующая цифра: 6 (больше 5).
3. Округлённое число: 9,86.

Пример 3. Округление чисел до ближайшей тысячной доли

Число: 3,14159

1. Округляем до тысячных.
2. Следующая цифра: 5 (равна 5).
3. Округлённое число: 3,142.

Приближение и округление чисел до определённого разряда

Когда округляем числа до определённого разряда, мы учитываем значение цифр в данной позиции и ближайшую к ним цифру. Это позволяет привести число к удобному формату.

Примеры округления до различных разрядов:

1. Округление числа 432,76 до сотен:

Поскольку 432,76 ближе к 400, чем к 500, округляем до 400.

2. Округление числа 987,65 до тысяч:

Поскольку 987,65 ближе к 1 000, чем к 900, округляем до 1000.

Округление чисел: примеры

1. Округление числа 4,6789 до двух знаков после запятой:

Смотрим на третью цифру после запятой (8). Поскольку 8 больше 5, округляем до 4,68.

2. Округление числа 5,434 до одного знака после запятой:

Смотрим на вторую цифру после запятой (4). Поскольку 4 меньше 5, округляем до 5,4.

3. Округление числа 0,999 до целого числа:

Поскольку 0,999 больше 0,5, округляем до 1.

4. Округление числа 12,345 до десятых:

Смотрим на вторую цифру после запятой (4). Поскольку 4 меньше 5, округляем до 12,3.

---

Округление чисел — это важный инструмент для упрощения расчётов и представления данных в удобном формате. Правильное понимание и применение правил округления поможет вам достигать точных и практичных результатов. Важно помнить, что округление должно соответствовать цели и контексту использования чисел, чтобы избежать ошибок и неточностей.

Если ребёнок испытывает трудности в округлении чисел, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия 💜

Первый урок с опытным репетитором — бесплатный, записывайтесь на него по форме ниже ⤵️