Натуральные числа

В 4–5 классах школьной программы ученики начинают знакомиться с важными математическими понятиями, такими как натуральные числа. Натуральные числа являются основой математики. Понимание их свойств и особенностей помогает детям развивать математическое мышление и решать разнообразные задачи.

В этой статье мы рассмотрим, что такое натуральные числа, как они записываются, их количественный смысл, разряды и системы счисления. А также научимся решать задачи с использованием натуральных чисел.

Определение натурального числа

Натуральные числа — это числа, которые используются для подсчёта и упорядочивания. Натуральные числа начинаются с 1 и продолжаются до бесконечности: 1, 2, 3, 4, 5 и так далее. Нуль не включается в множество натуральных чисел. Эти числа мы встречаем ежедневно: когда считаем предметы, описываем их количество или говорим о порядке.

Десятичная запись натурального числа

Каждое натуральное число можно записать в десятичной системе счисления, используя десятичные цифры от 0 до 9. Десятичная система счисления — это основная система записи чисел, которой мы пользуемся в повседневной жизни. Например, число 345 состоит из цифр 3, 4 и 5, каждая из которых имеет своё значение в зависимости от позиции в числе. Эта система удобна и универсальна, что делает её такой распространённой.

Количественный смысл натуральных чисел

Натуральные числа используются для обозначения количества объектов. Например, число 3 в словосочетании «3 яблока» указывает на количество яблок. Это называется количественным смыслом числа. Используя натуральные числа, мы можем точно определить, сколько предметов у нас есть или сколько нужно добавить, чтобы получить определённое количество.

Однозначные, двузначные, трёхзначные натуральные числа

Натуральные числа до 1 000 можно разделить на однозначные, двузначные и трёхзначные:

1. Однозначные числа: 1, 2, 3, …, 9. Это самые простые числа, которые состоят из одной цифры.
2. Двузначные числа: 10, 11, 12, …, 99. Эти числа состоят из двух цифр, где первая цифра обозначает десятки, а вторая — единицы.
3. Трёхзначные числа: 100, 101, 102, …, 999. Здесь первая цифра обозначает сотни, вторая — десятки, а третья — единицы.

Многозначные натуральные числа

Натуральные числа, содержащие четыре и более цифр, называются многозначными. Например, числа 1 000, 12 345 и 987 654 являются многозначными числами. Такие числа используются для обозначения больших количеств. Например, в больших городах численность населения выражается многозначными числами.

Свойства натуральных чисел

Натуральные числа обладают следующими свойствами:

➤ Сложение и умножение

Натуральные числа замкнуты относительно сложения и умножения, то есть сумма или произведение любых двух натуральных чисел также является натуральным числом. Например, если мы сложим 2 и 3, мы получим 5 — это тоже натуральное число.

➤ Ассоциативность и коммутативность

Для любых натуральных чисел a, b и c выполняются свойства: a + (b + c) = (a + b) + c и a ∙ (b ∙ c) = (a ∙ b) ∙ c, а также a + b = b + a и a ∙ b = b ∙ a. Это значит, что порядок сложения или умножения не влияет на результат.

➤ Существование наименьшего элемента

В множестве натуральных чисел существует наименьшее число — 1. Это самое маленькое натуральное число, с которого начинается весь ряд натуральных чисел.

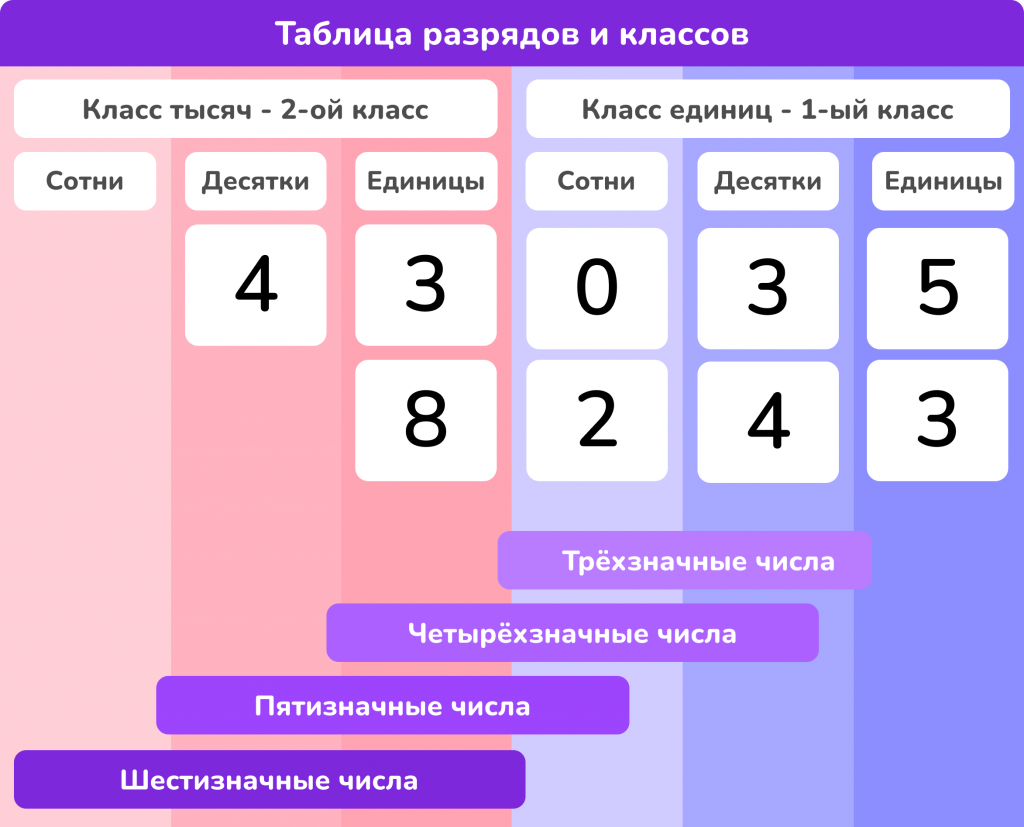
Разряды натурального числа и значение разряда

Каждое натуральное число можно разложить на разряды. Разряды показывают, сколько единиц, десятков, сотен и так далее содержит число. Например, в числе 345:

1. 5 — количество единиц;
2. 4 — количество десятков;
3. 3 — количество сотен.

Это разложение помогает понять, из каких компонентов состоит число и как его можно представить в виде суммы разрядных слагаемых.

Представление натурального числа в виде суммы разрядных слагаемых

Натуральное число можно представить как сумму разрядных слагаемых. Например, число 345 можно представить как: 345 = 300 + 40 + 5.

Это позволяет легко работать с числами и понимать их внутреннюю структуру.

Десятичная система счисления

Десятичная система счисления — это система, в которой для записи чисел используются десятичные цифры (0–9) и каждый разряд числа представляет собой степень числа 10.

Например, число 345 в десятичной системе означает: 345 = 3 ∙ 10² + 4 ∙ 10¹ + 5 ∙ 10⁰.

Эта система удобна для арифметических операций и широко используется во всём мире.

Решение задач с натуральными числами

Рассмотрим несколько примеров задач для лучшего понимания натуральных чисел.

✔ Задача 1. Найдите сумму чисел 345 и 678. 

345 + 678 = 1023.

✔ Задача 2. Найдите произведение чисел 12 и 34. 

12 ∙ 34 = 408

✔ Задача 3. Представьте число 789 в виде суммы разрядных слагаемых. 

789 = 700 + 80 + 9.

✔ Задача 4. Найдите разность чисел 1 000 и 753.

1000 — 753 = 247.

✔ Задача 5. Какое число является наибольшим трёхзначным числом?

Наибольшее трёхзначное число — 999.

✔ Задача 6. Сколько существует трёхзначных чисел?

Количество трёхзначных чисел = 999 – 100 + 1 = 900.

✔ Задача 7. Сколько существует двузначных чисел?

Количество двузначных чисел = 99 − 10 + 1 = 90.

✔ Задача 8. Найдите разность между наибольшим двузначным числом и наименьшим трёхзначным числом.

Наибольшее двузначное число — это 99, а наименьшее трёхзначное число — 100. Разность между ними: 100 − 99 = 1.

Итак, нам удалось узнать:

1. Натуральные числа — это числа, используемые для подсчёта и упорядочивания, начиная с 1.
2. Каждое натуральное число можно записать в десятичной системе счисления, используя цифры от 0 до 9.
3. Натуральные числа имеют количественный смысл и делятся на однозначные, двузначные, трёхзначные и многозначные.
4. Натуральные числа обладают свойствами ассоциативности и коммутативности для сложения и умножения.
5. Разряды натурального числа показывают количество единиц, десятков, сотен и так далее.
6. Натуральное число можно представить в виде суммы разрядных слагаемых.
7. Десятичная система счисления использует степени числа 10 для представления каждого разряда.

Если ребёнок испытывает трудности в понимании натуральных чисел, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия 💜