Логические выражения

В этой статье мы изучим одну из самых интересных и практичных тем в информатике — логические выражения. Знание логики необходимо не только программистам, но и всем, кто хочет развить аналитическое мышление и научиться принимать обоснованные решения.

Логика — это наука о законах и формах правильного мышления. В информатике логика помогает компьютеру «думать» и принимать решения на основе определённых условий. Например, представьте, что вы решаете, идти ли гулять. Ваше решение зависит от нескольких условий: «Если на улице тепло И нет дождя, ТО я пойду гулять». Это и есть логическое выражение!

Программирование неразрывно связано с логикой. Каждый раз, когда вы пишете, например, условие в программе (например, if age > 18), вы используете логические выражения. Без них невозможно представить современные программы и алгоритмы.

Основные понятия логики

1. Логическое высказывание

— это повествовательное предложение, которое может быть либо истинным (True), либо ложным (False).

Примечание: если высказывание истинно, то принято обозначение 1, если ложно — 0.

Примеры истинных высказываний:

1. «2 + 2 = 4».
2. «Москва — столица России».
3. «В неделе 7 дней».

Примеры ложных высказываний:

1. «Земля плоская».
2. «5 > 10».
3. «Зимой всегда идёт снег».

Приведём примеры выражений, которые НЕ являются высказываниями (про каждое из них невозможно сказать истинно оно или ложно):

1. «Закрой дверь!» (повелительное).
2. «Какой сегодня день?» (вопросительное).
3. «Ура!» (восклицание).

2. Простые и составные высказывания

Простые высказывания содержат одну законченную мысль.

Например: «Сегодня солнечно».

Составные высказывания образуются из простых с помощью логических операций.

Например: «Сегодня солнечно И тепло».

Логические операции

1. Логическое И (конъюнкция)

Обозначение: ∧, AND, &.

Конъюнкция истинна только тогда, когда ОБА высказывания истинны.

Таблица истинности для конъюнкции:

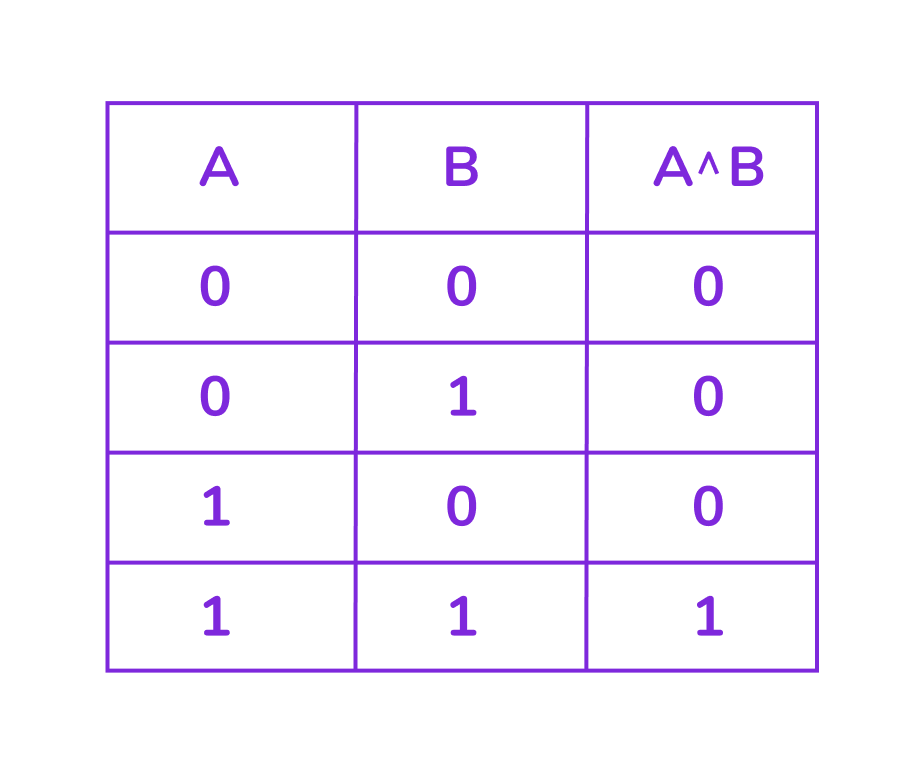
Пример:

1. «Я люблю математику И информатику» — истинно только тогда, когда истинно высказывание «Я люблю математику» и истинно высказывание «Я люблю информатику».

2. Логическое ИЛИ (дизъюнкция)

Обозначение: ∨, OR, |.

Дизъюнкция ложна только тогда, когда ОБА высказывания ложны.

Таблица истинности для дизъюнкции:

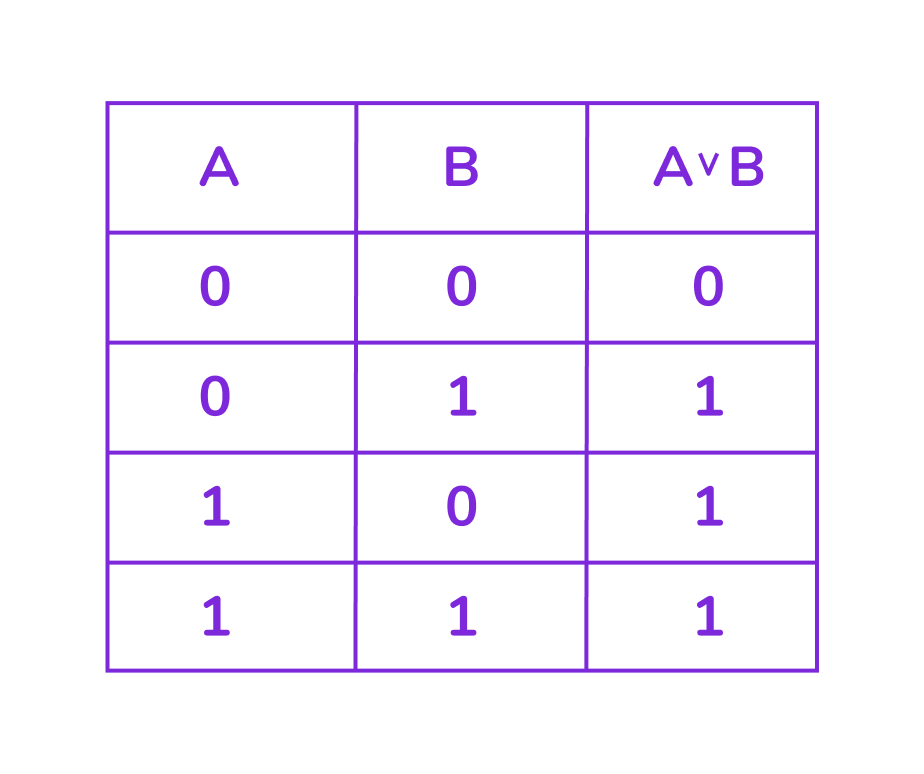
Примеры:

1. «Я пойду в кино ИЛИ в театр» — истинно, если пойдут хотя бы в одно место.
2. «Завтра будет дождь ИЛИ снег» — ложно, только если не будет ни дождя, ни снега.

3. Логическое НЕ (отрицание)

Обозначение: ¬, NOT, !.

Отрицание меняет значение высказывания на противоположное.

Таблица истинности для логического отрицания:

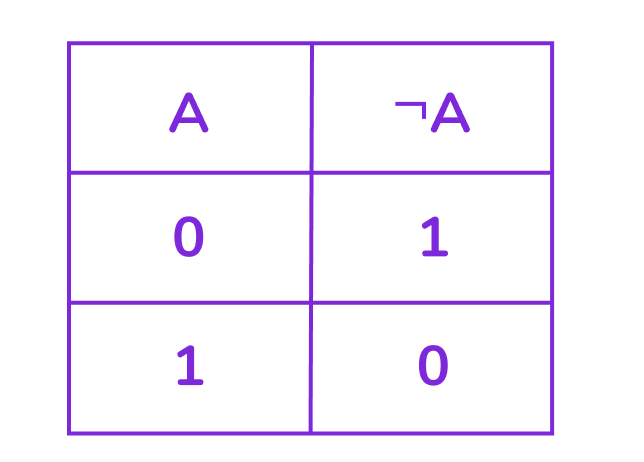
Примеры:

1. «НЕ сегодня понедельник» — истинно во все дни, кроме понедельника.
2. «НЕ (2 + 2 = 5)» — истинно, так как 2+2≠5.

Приоритет логических операций

Всегда важно соблюдать порядок выполнения логических операций:

1. Скобки — всегда выполняются первыми.

2. Отрицание (НЕ) — ¬A.

3. Конъюнкция (И) — A ∧ B.

4. Дизъюнкция (ИЛИ) — A ∨ B.

Примеры:

1. ¬A ∧ B = (¬A) ∧ B.
2. A ∨ B ∧ C = A ∨ (B ∧ C).
3. ¬(A ∧ B) — сначала выполняется операция в скобках, затем отрицание.

Важно! Всегда используйте скобки, если есть сомнения в порядке выполнения операций.

Логические выражения: примеры решения заданий

Задание 1

Составьте логическое выражение для ситуации, необходимой для похода на улицу. Если имеется следующее условие: «Я пойду на прогулку, если будет хорошая погода И я сделаю уроки, ИЛИ если меня позовут друзья».

Решение

Обозначим:

1. П: «Хорошая погода».
2. У: «Уроки сделаны».
3. Д: «Друзья позвали».

Логическое выражение: (П ∧ У) — «Хорошая погода» И «Уроки сделаны».

Логическое выражение: (П ∧ У) ∨ Д — («Хорошая погода» И «Уроки сделаны») ИЛИ «Друзья позвали».

Ответ:  (П ∧ У) ∨ Д.

Задание 2

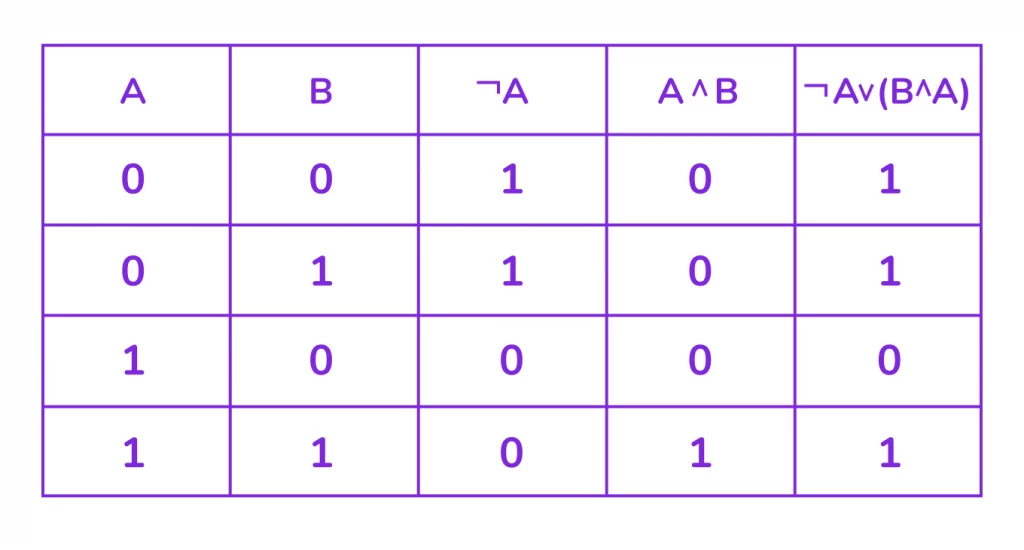
Составьте таблицу истинности для выражения: ¬A ∨ (B ∧ A).

Решение:

1. Столбцы A и B: это все возможные комбинации значений двух переменных.

2. Столбец ¬A (НЕ A): значение, противоположное A.

3. Столбец B ∧ A (B И A): логическое И. Результат истинен (1), только когда и B, и A истинны.

4. Столбец ¬A ∨ (B ∧ A) (НЕ A ИЛИ (B И A)): логическое ИЛИ. Результат истинен (1), если истинно хотя бы одно из выражений: ¬A или (B ∧ A).

📝 Упражнение для самопроверки

Упражнение. Определите, являются ли высказываниями выражения:
а) «Птицы летают».
б) «Будь внимательным!».
в) «7 — простое число».

Ответы:

а) да; б) нет; в) да.

Подведём итоги

Мы изучили важную тему «Логические выражения», знание которой нужно будет как при дальнейшем изучении информатики, так и при сдачи экзамена.

Нам удалось узнать:

1. Логические выражения позволяют формализовать сложные условия.
2. Основные операции: И, ИЛИ, НЕ.
3. Таблицы истинности помогают анализировать сложные выражения.
4. Знание логики необходимо для программирования.