
Квадратичная функция: построение параболы
Квадратичная функция является одной из важнейших тем в курсе алгебры 8–9-х классов. Она помогает понять, как строить графики, анализировать их свойства и решать задачи, связанные с реальными ситуациями. График квадратичной функции называется параболой и имеет множество практических применений: от описания траектории движения тела до моделирования экономических процессов.
В этой статье мы рассмотрим основные определения, способы построения параболы и алгоритмы работы с разными формами уравнений квадратичной функции.

Основные определения
📎 Квадратичная функция — это функция вида y = ax² + bx + c , где a = 0, x — независимая переменная, y — зависимая переменная, а a, b, c — коэффициенты.
График квадратичной функции — это парабола:
- Если a > 0 , то ветви параболы направлены вверх.
- Если a < 0 , то ветви параболы направлены вниз.
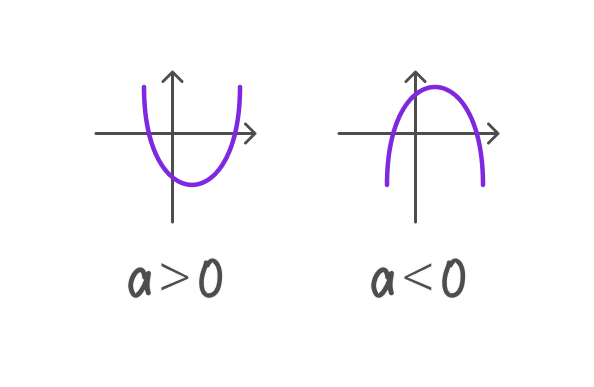
📎 Вершина параболы — это точка, в которой парабола достигает своего минимума (если a > 0 ) или максимума (если a < 0). Координаты вершины находятся по формулам:
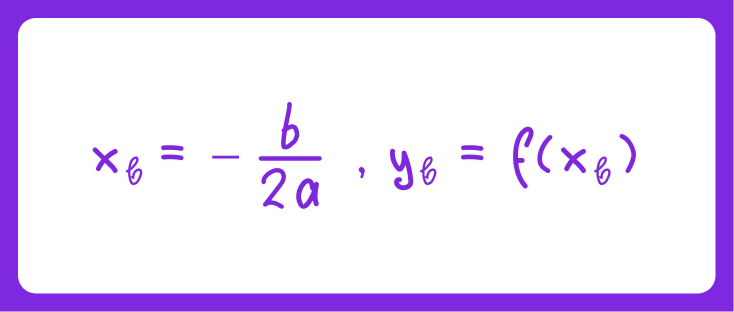
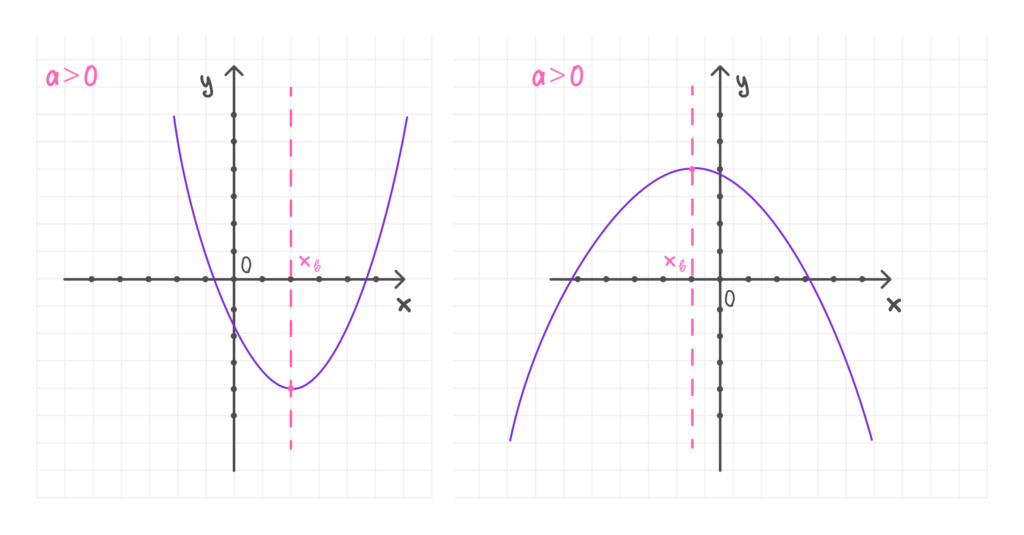
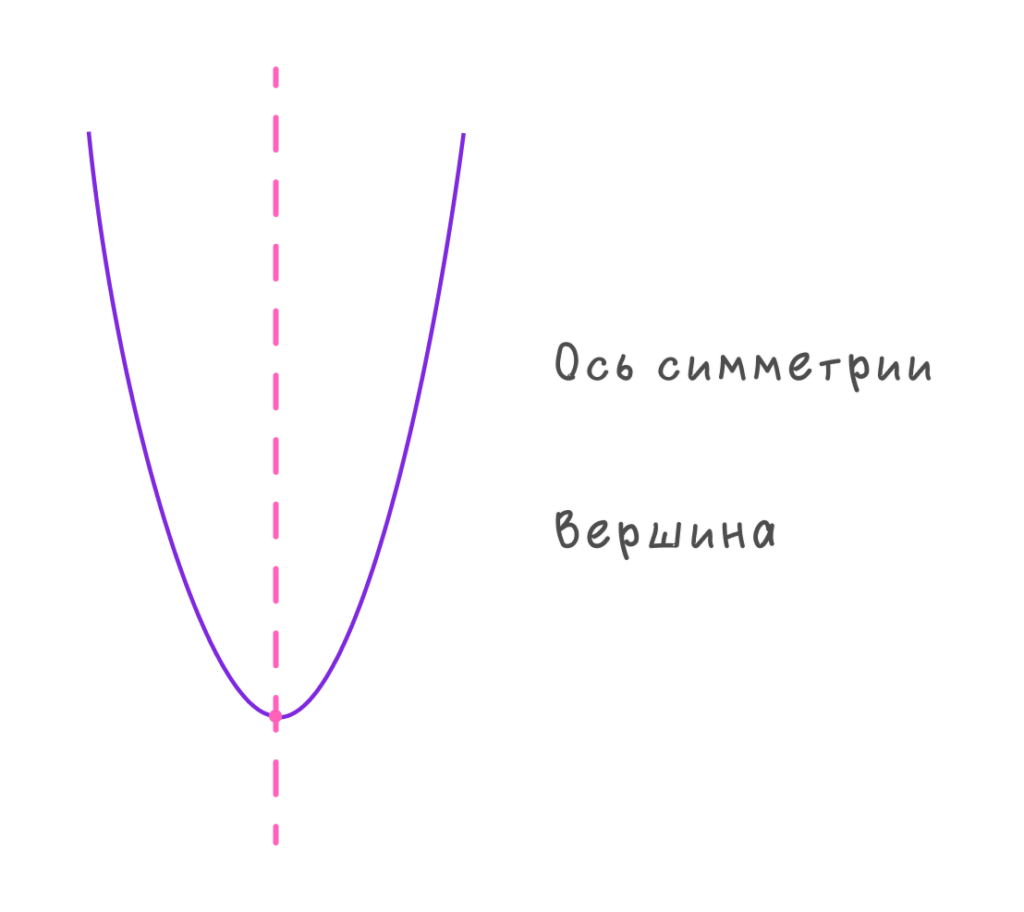
📎 Ось симметрии параболы — это вертикальная прямая, проходящая через вершину параболы, заданная уравнением x = xв.
📎 Нули функции — это точки пересечения графика с осью абсцисс (Ox), которые находятся как корни уравнения ax² + bx + c = 0.
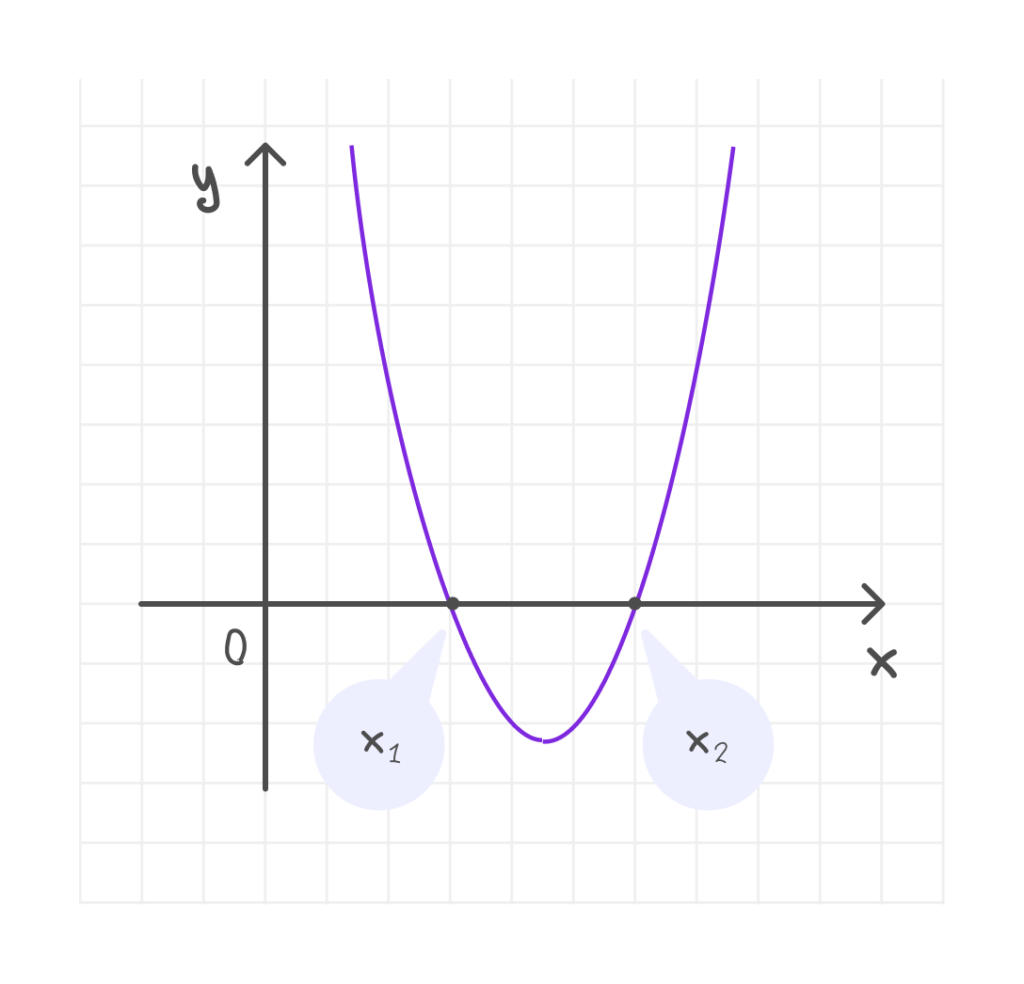
Построение квадратичной функции
Для построения графика квадратичной функции необходимо выполнить следующие шаги ⤵
1. Определение направления ветвей параболы:
- Если a > 0 , ветви направлены вверх.
- Если a < 0 , ветви направлены вниз.
2. Нахождение координат вершины параболы:
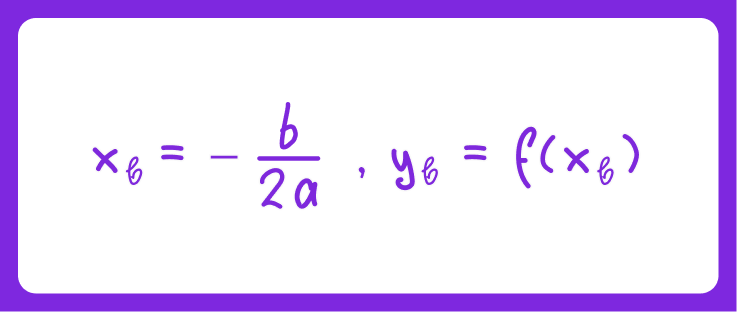
3. Вычисление дискриминанта D = b² − 4ac:
- Если D > 0 , то парабола пересекает ось Ox в двух точках.
- Если D = 0 , то парабола касается оси Ox в одной точке.
- D < 0 , то парабола не пересекает ось Ox.
4. Нахождение точек пересечения с осями координат:
- Точка пересечения с осью Oy: y(0) = c.
- Точки пересечения с осью Ox: решите уравнение ax² + bx + c = 0.
5. Построение дополнительных точек.
Составьте таблицу значений функции для нескольких значений x.
6. Построение графика.
Нанесите все найденные точки на координатную плоскость и соедините их плавной линией.
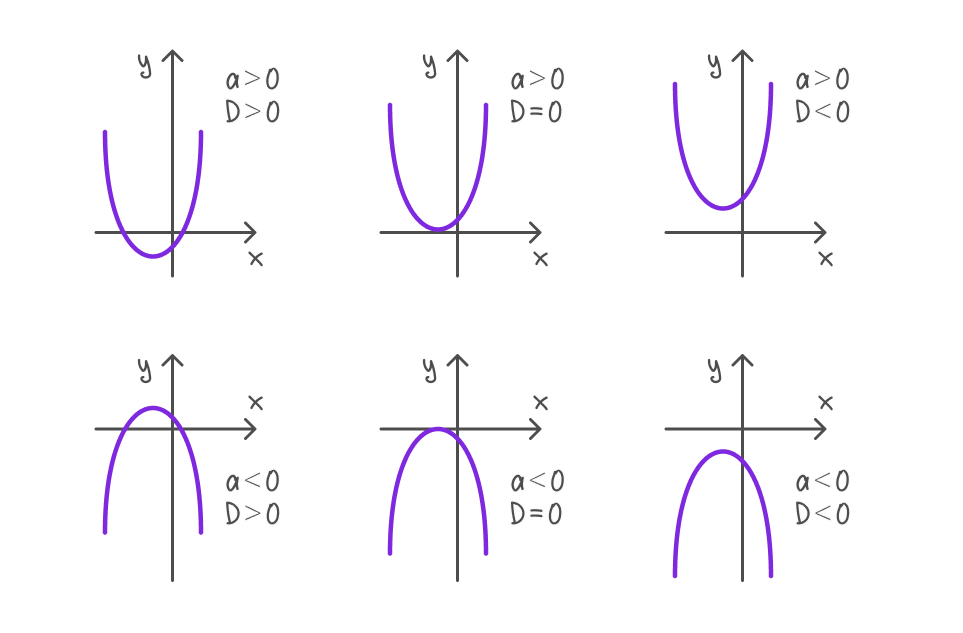
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы в зависимости от формы уравнения. Наиболее удобный способ выбирается в соответствии с тем, как задана квадратичная функция.
1️⃣ Уравнение квадратичной функции имеет вид y = ax² + bx + c
1. Определить направление ветвей параболы:
- Если a > 0, ветви направлены вверх.
- Если a < 0, ветви направлены вниз.
2. Найти дискриминант D = b² — 4ac:
- Если D > 0, парабола пересекает ось Ox в двух точках.
- Если D = 0, парабола касается оси Ox в одной точке.
- D < 0, парабола не пересекает ось Ox.
3. Найти координаты вершины параболы:
- Абсцисса вершины: x₀ = -b/(2a).
- Ордината вершины: y₀ = f(x₀).
4. Найти точки пересечения с осями координат:
- С осью Oy: подставить x = 0 в уравнение, y(0) = c.
- С осью Ox: решить уравнение ax² + bx + c = 0.
5. Построить график:
- Нанести вершину, точки пересечения с осями и дополнительные точки.
- Соединить их плавной линией.
Пример
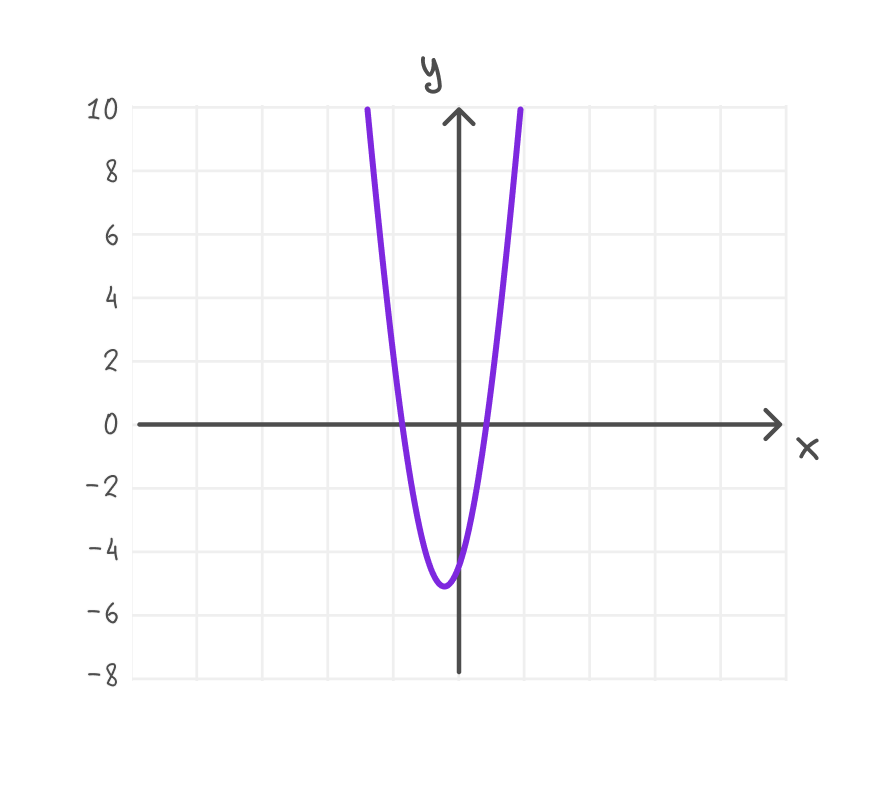
Построить график функции y = 2x² + 3x — 5:
1) a = 2 > 0, ветви направлены вверх.
2) D = 3² — 4 ⋅ 2 ⋅ (-5) = 49 > 0. Корни: x₁ = -2,5, x₂ = 1.
3) Вершина: x₀ = -3 / (2 ⋅ 2) = -0,75, y₀ = 2 ⋅ (-0,75)² + 3 ⋅ (-0,75) — 5 = -6,125.
4) Точка пересечения с Oy: (0; -5).
2️⃣ Уравнение квадратичной функции имеет вид y = a(x — x₀)² + y₀
1. Определить координаты вершины параболы:
- Вершина: (x₀; y₀).
2. Определить направление ветвей параболы:
- Если a > 0, ветви направлены вверх.
- Если a < 0, ветви направлены вниз.
3. Найти точку пересечения с осью Oy:
- Подставить x = 0 в уравнение, y(0) = a(0 — x₀)² + y₀.
4. Найти дополнительные точки:
- Подставить несколько значений x в уравнение для нахождения соответствующих значений y.
5. Построить график:
- Нанести вершину, точку пересечения с Oy и дополнительные точки.
- Соединить их плавной линией.
Пример
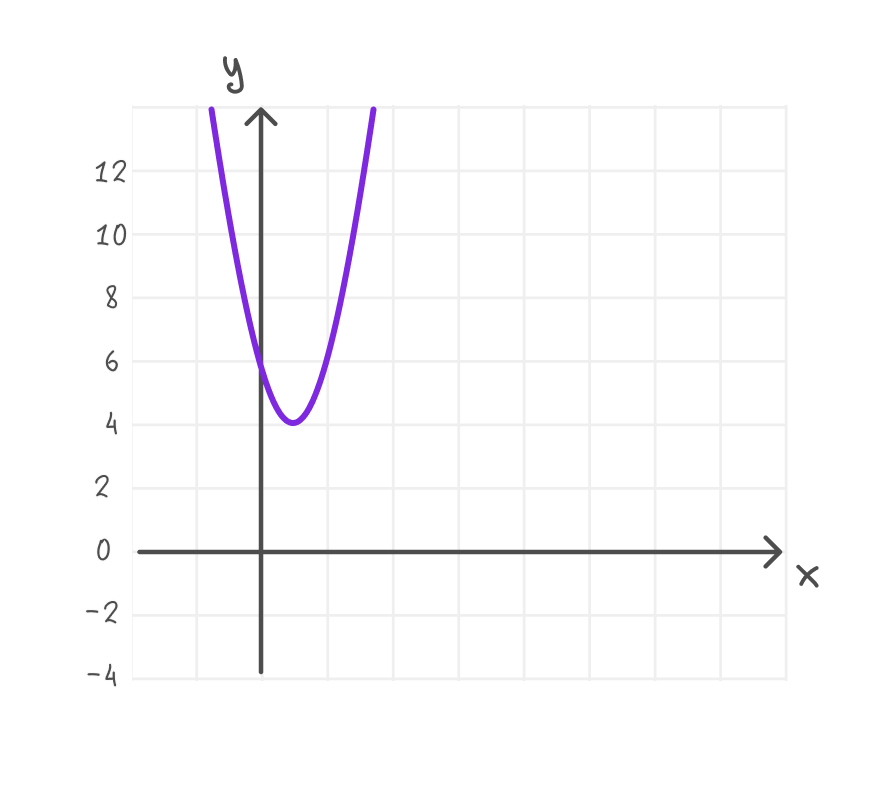
Построить график функции y = 2(x — 1)² + 4:
1) Вершина: (1; 4).
2) Ветви направлены вверх (a = 2 > 0).
3) Точка пересечения с Oy: y(0) = 2(0 — 1)² + 4 = 6.
3️⃣ Уравнение квадратичной функции имеет вид y = (x + a)(x + b)
1. Найти нули функции:
- Решить уравнение (x + a)(x + b) = 0.
- Нули: x₁ = -a, x₂ = -b.
2. Определить координаты вершины параболы:
- Абсцисса вершины: x₀ = (x₁ + x₂) / 2.
- Ордината вершины: y₀ = f(x₀).
3. Найти точку пересечения с осью Oy:
- Подставить x = 0 в уравнение, y(0) = (0 + a)(0 + b).
4. Построить график:
- Нанести вершину, нули функции и точку пересечения с Oy.
- Соединить их плавной линией.
Пример
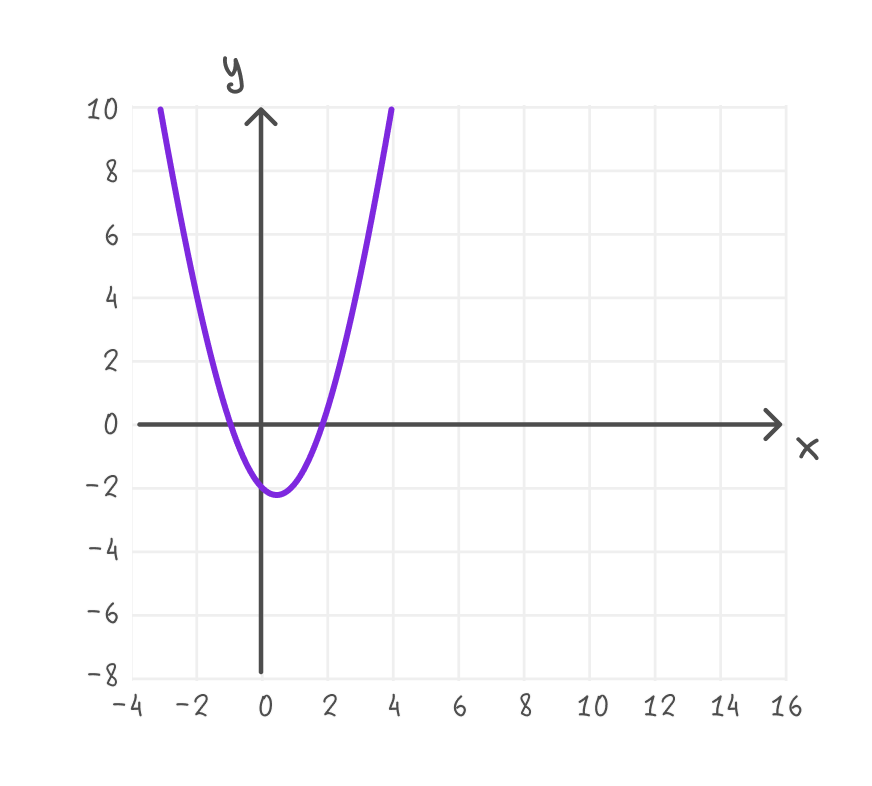
Построить график функции y = (x — 2)(x + 1):
1) Нули: x₁ = 2, x₂ = -1.
2) Вершина: x₀ = (2 + (-1)) / 2 = 0,5, y₀ = (0,5 — 2)(0,5 + 1) = -2,25.
3) Точка пересечения с Oy: y(0) = (0 — 2)(0 + 1) = -2.
Квадратичная функция — это мощный инструмент для анализа и моделирования различных явлений. График квадратичной функции (парабола) позволяет наглядно представить поведение функции и её свойства. Основные этапы построения параболы включают определение направления ветвей, нахождение вершины, вычисление нулей функции и точек пересечения с осями координат. Знание различных форм записи уравнения квадратичной функции позволяет эффективно решать задачи и строить графики.
Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы. Первый урок по форме ниже — бесплатный!
 14
14
 7
7
 4
4








Как строить параболы y=-2x²+5x+3?