Конус и его свойства

Сегодня мы погрузимся в изучение одной из самых элегантных и практически значимых фигур в стереометрии — конуса. Эта фигура объединяет в себе красоту математической формы и широкое практическое применение в различных сферах человеческой деятельности.

Историческая справка: конус был известен ещё древним грекам. Евклид в своих «Началах» дал одно из первых определений этой фигуры. Архимед глубоко изучал свойства конических сечений, а Аполлоний Пергский посвятил им целый трактат. Интересно, что многие природные объекты — вулканы, смерчи, кроны деревьев — имеют коническую форму, что демонстрирует фундаментальность этой геометрической фигуры в природе.

Практическая значимость конуса:

1. Архитектура и строительство: купола зданий, башни, шпили.
2. Техника: конические шестерни, резьбовые соединения, сопла двигателей.
3. Природа: вулканы, раковины моллюсков, кроны хвойных деревьев.
4. Промышленность: бункеры для сыпучих материалов, дозаторы.
5. Дизайн: элементы декора, посуда, осветительные приборы.

Коническая поверхность

Прежде чем перейти к конусу, рассмотрим более общее понятие — коническую поверхность.

Конической поверхностью называется поверхность, образованная движением прямой линии (образующей), которая проходит через неподвижную точку (вершину) и пересекает заданную линию (направляющую).

Математическое описание
Если направляющая задана уравнением f(x,y,z) = 0, а вершина находится в точке A(x₀,y₀,z₀), то коническая поверхность состоит из всех точек, лежащих на прямых, соединяющих вершину с точками направляющей.

Примеры конических поверхностей:

1. Круговой конус (направляющая — окружность).
2. Эллиптический конус (направляющая — эллипс).
3. Параболический конус (направляющая — парабола).

Определение конуса. Прямой круговой конус

Конус — это тело, ограниченное конической поверхностью и плоскостью, пересекающей все образующие этой поверхности.

Классификация конусов:

1. Прямой конус: ось конуса перпендикулярна плоскости основания.
2. Наклонный конус: ось не перпендикулярна основанию.
3. Круговой конус: основание — круг.
4. Эллиптический конус: основание — эллипс.

В школьном курсе стереометрии преимущественно изучается прямой круговой конус.

Прямой круговой конус

Рассмотрим подробно прямой круговой конус — наиболее распространённый тип конуса (Рисунок 1).

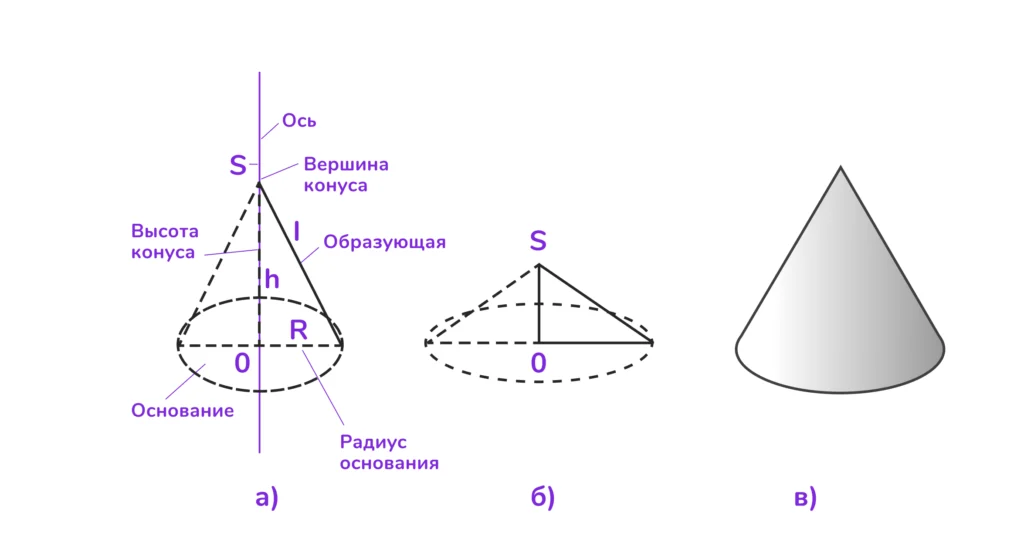
Основные элементы конуса

1. Вершина (S) — точка, в которой сходятся все образующие конуса. Это «остриё» конуса.
2. Основание — плоская фигура (круг), которая ограничивает конус снизу. Центр основания обозначается точкой O.
3. Образующая (l) — отрезок, соединяющий вершину конуса с точкой на окружности основания. Все образующие прямого кругового конуса равны между собой.
4. Высота (h) — перпендикуляр, опущенный из вершины конуса на плоскость основания. В прямом конусе высота проходит через центр основания.
5. Ось конуса — прямая, содержащая высоту конуса. В прямом круговом конусе ось является осью симметрии.
6. Радиус основания (R) — радиус круга, являющегося основанием конуса.
7. Боковая поверхность — коническая поверхность, ограничивающая конус с боков.

Соотношения между элементами конуса (Рисунок 1(а))

Для прямого кругового конуса выполняется соотношение, связывающее образующую, высоту и радиус основания:

l²=h²+R²

Это соотношение непосредственно следует из теоремы Пифагора, применённой к прямоугольному треугольнику, образованному высотой, радиусом и образующей.

Прямой круговой конус является телом вращения. Его определение, как тела вращения, следующее: 

Прямой круговой конус — это тело, полученное при вращении прямоугольного треугольника вокруг одной из его сторон, содержащей прямой угол (Рисунок 1(б, в)).

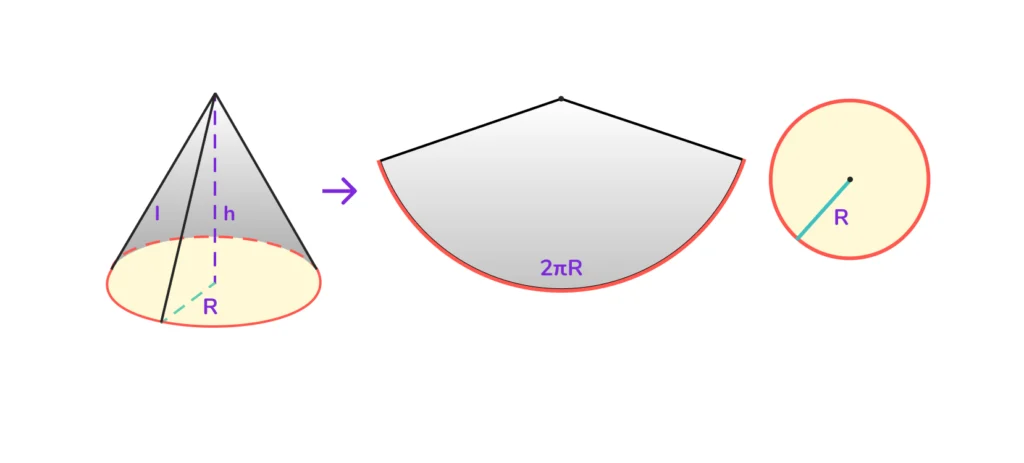
Развёртка конуса

Развёртка прямого кругового конуса — это плоская фигура, состоящая из:

1. круга (развёртка основания);
2. кругового сектора (развёртка боковой поверхности).

Радиус боковой поверхности (сектора) равен образующей конуса l.

Длина дуги сектора равна длине окружности основания L=2πR, где R — радиус основания конуса.

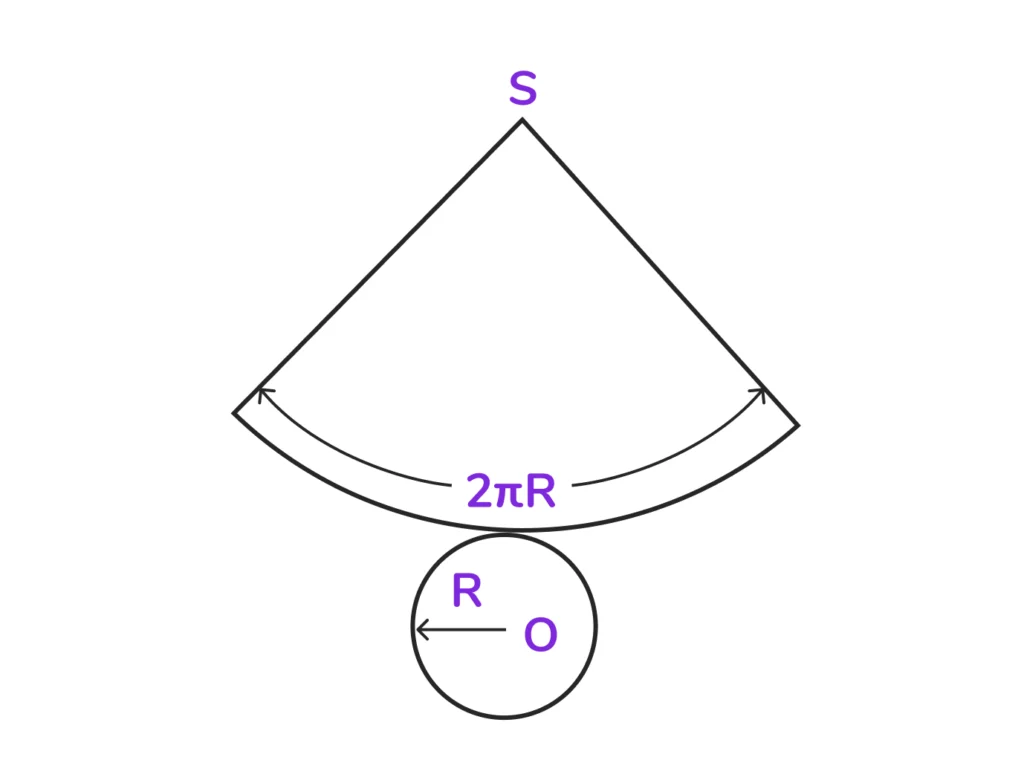
Развёртка конуса имеет широкое практическое применение, используется при изготовлении конических объектов из листовых материалов — воронок, колпаков, декоративных элементов.

Площади боковой и полной поверхностей. Объём конуса

Площадь боковой поверхности

Формула площади боковой поверхности:

S_бок=πRl

где R — радиус основания, l — образующая конуса.

Вывод формулы

Площадь боковой поверхности конуса равна площади сектора круга с радиусом l и длиной дуги 

S_бок=½⋅l⋅(2πR)=πRl

Площадь полной поверхности

Формула площади полной поверхности:

S_полн=S_бок+S_осн=πRl+πR²=πR(l+R)

таким образом:

S_полн=πR(l+R)

Объём конуса

Формула объёма:

V=⅓πR²h

где R — радиус основания, h — высота конуса.

Примеры решения задач

Задача 1. Найдите площадь полной поверхности конуса, если его образующая равна 10 см, а радиус основания — 6 см.

Решение:

S_полн=πR(l+R)=π⋅6⋅(10+6)=6π⋅16=96π см²

Ответ: 96π см².

Задача 2. Высота конуса равна 12 см, радиус основания — 5 см. Найдите объём конуса.

Решение:

V=⅓πR²h=⅓π⋅25⋅12=100π см³

Ответ: 100π см³.

📝 Упражнение для самопроверки

Упражнение. Конус имеет высоту 8 см и образующую 10 см. Найдите площадь боковой поверхности.

Решение:
Сначала найдём радиус основания конуса:

R²=l²−h²=100−64=36, отсюда R=6 см

Теперь найдём площадь боковой поверхности:

S_бок=πRl=π⋅6⋅10=60π см²

Подведём итоги

Мы изучили одну из ключевых фигур стереометрии — конус. Это знание будет востребовано не только на экзаменах, но и в дальнейшей учебной и профессиональной деятельности.

Подведём итоги:

1. Прямой круговой конус — это тело вращения, обладающее осевой симметрией.
2. Основные элементы конуса: вершина, основание, образующая, высота.
3. Формулы для вычисления площадей поверхностей и объёма основаны на свойствах круга и теореме Пифагора.
4. Развёртка конуса позволяет создавать конические объекты из плоских материалов.

Знания о конусе будут полезны при изучении математического анализа (конические сечения), физики (траектории движения), инженерного дела (проектирование механизмов), архитектуры (проектирование куполов).

Для успешного освоения темы внимательно изучите взаимосвязи между элементами конуса; освойте построение развёртки конуса; решайте разнообразные задачи на вычисление площадей и объёмов; обращайте внимание на практические приложения теории. А также развивайте пространственное воображение: обращайте внимание на конические формы в окружающем мире. И помните: геометрия — это не только наука, но и искусство видеть гармонию в формах окружающего мира.