Иррациональные числа

В этой статье мы познакомимся с иррациональными числами. Их невозможно записать в виде обыкновенной дроби, но они постоянно встречаются в реальной жизни. Например, когда вы вычисляете длину диагонали квадрата или длину окружности, то сталкиваетесь именно с иррациональными числами. Давайте вместе разберёмся, что это за числа и как с ними работать.

Определение и примеры иррациональных чисел

Иррациональные числа — это числа, которые нельзя представить в виде обыкновенной дроби m/n, где m — целое число, а n — натуральное. Их десятичная запись бесконечна и не периодична.

Иррациональные числа уже встречались вам ранее на уроках математики. Вот некоторые примеры:

1. √2 = 1,414213562… (длина диагонали квадрата со стороной 1);
2. π = 3,141592653… (отношение длины окружности к её диаметру).

Множество иррациональных чисел

Иррациональные числа обозначаются буквой I. Вместе с рациональными числами (Q) они образуют множество действительных чисел (R).

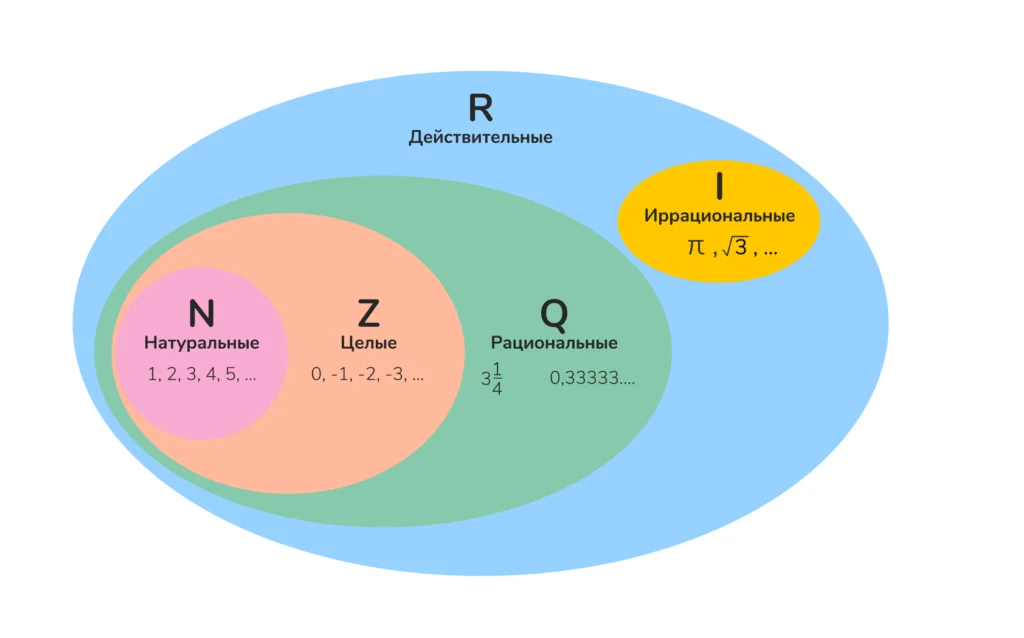
1. Натуральные числа (N): 1, 2, 3…
2. Целые числа (Z): …-2, -1, 0, 1, 2…
3. Рациональные числа (Q): дроби m/n
4. Иррациональные числа (I): √2, π…
5. Действительные числа (R): все вышеперечисленные.

Действия с иррациональными числами

С иррациональными числами можно выполнять арифметические действия: сложение, вычитание, умножение и деление.

Например:

1. √2 + √2 = 2√2;
2. √3 × √3 = 3;
3. √8 = 2√2 (вынесение множителя из под знака корня).

На практике могут потребоваться приближённые значения, например:

1. √2 ≈ 1,41;
2. π ≈ 3,14;
3. √3 ≈ 1,73.

Примеры решения заданий

Давайте посмотрим, как решать задания с иррациональными числами.

Задание 1. Какие из этих чисел являются иррациональными: √4; √5; π; 0,333…; ⅔ ?

Решение: 

1. √4 = 2 — натуральное число;
2. √5 — иррациональное число;
3. π — иррациональное число;
4. ⅓ = 0,333… — рациональное число;
5. ⅔ — рациональное число.

Ответ:  √5, π.

Задание 2. Вычислите: (√3 + 2)².

Решение:
(√3 + 2)² = (√3)² + 2×√3×2 + 2² = 3 + 4√3 + 4 = 7 + 4√3.

Ответ: 7 + 4√3.

📝 Упражнение для самопроверки

Упражнение 1. Упростите выражение: √12 + √27.

Решение: √12 + √27 = 2√3 + 3√3 = 5√3.

Ответ: 5√3.

Иррациональные числа — это важная часть математики, которая находит применение в геометрии, физике и инженерии. Они помогают точно описывать реальный мир, где многие величины невозможно выразить обыкновенными дробями.