График линейной функции

В математике очень часто приходится описывать зависимости между величинами. Например, чем больше километров вы проезжаете на автомобиле, тем больше топлива расходуется. Чем больше вы работаете, тем выше заработок (если оплата почасовая). Такие зависимости удобно выражать с помощью функций.

Одним из самых простых и часто встречающихся типов зависимостей является линейная функция. Она лежит в основе многих тем школьного курса алгебры, физики, экономики и даже информатики. Понимание того, как выглядит график линейной функции, как его построить и проанализировать, — важный шаг на пути к освоению более сложных математических понятий.

Понятие функции

Перед тем как изучать линейные функции, нужно понять, что такое функция вообще.

Функция — это правило, по которому каждой величине x (аргументу) ставится в соответствие единственное значение y (значение функции).

Например: если вы покупаете яблоки по цене 100 рублей за килограмм, то стоимость покупки y зависит от массы x: y = 100x.

1. если x = 1 кг, то y = 100 руб.;
2. если x = 2 кг, то y = 200 руб.

Здесь x — аргумент функции (масса яблок), y — значение функции (стоимость), а правило «умножить на 100» задаёт саму функцию.

Можно сказать, что функция — это как «машина», которая на входе получает число x, а на выходе выдаёт число y, рассчитанное по определённому правилу.

Работая с функциями, нужно понимать — каковы её область определения и область значений. Разберёмся с этими понятиями подробнее ⤵

Область определения функции — это множество всех значений независимой переменной (аргумента) x, при которых функция имеет смысл.

Простыми словами: это все числа, которые можно подставить вместо x в формулу функции.

Область значений функции — это множество всех значений зависимой переменной (функции) y, которые принимает функция при всех допустимых значениях x.

Простыми словами: это все числа, которые может принимать y, когда x «пробегает» всю область определения.

Понятие линейной функции

Линейная функция — это функция, которую можно записать в виде:

y = kx + b, где k и b — некоторые числа.

График линейной функции всегда является прямой линией.

k и b имеют названия:

1. k — коэффициент наклона (угловой коэффициент);
2. b — свободный член, который показывает, где прямая (график линейной функции) пересекает ось OY.

График линейной функции и его построение

График функции — это множество всех точек (x, y), координаты которых удовлетворяют уравнению функции.

Для линейной функции y = kx + b все такие точки образует прямую линию.

👉 Рассмотрим пошаговый алгоритм построения графика линейной функции ⤵

Шаг 1. Определим коэффициенты k и b.

Рассмотрим, к примеру, функцию y = 2x + 1.
Здесь k = 2, b = 1.

Шаг 2. Найдём две точки, которые принадлежат графику.

Достаточно подставить любое числовое значение вместо x и вычислить y.

Например, при x = 0 посчитаем чему равен у:  

1. y = 2⋅0 + 1 = 1, получили точку с координатами (0; 1), которая принадлежит графику рассматриваемой функции;
2. при x = 2, y = 2⋅2 + 1 = 5, таким образом, точка с координатами (2; 5) также принадлежит графику нашей функции.

Шаг 3. Отметим точки на координатной плоскости.

Построим координатную плоскость. Отметим на ней точки (0; 1) и (2; 5) (Рисунок 1).

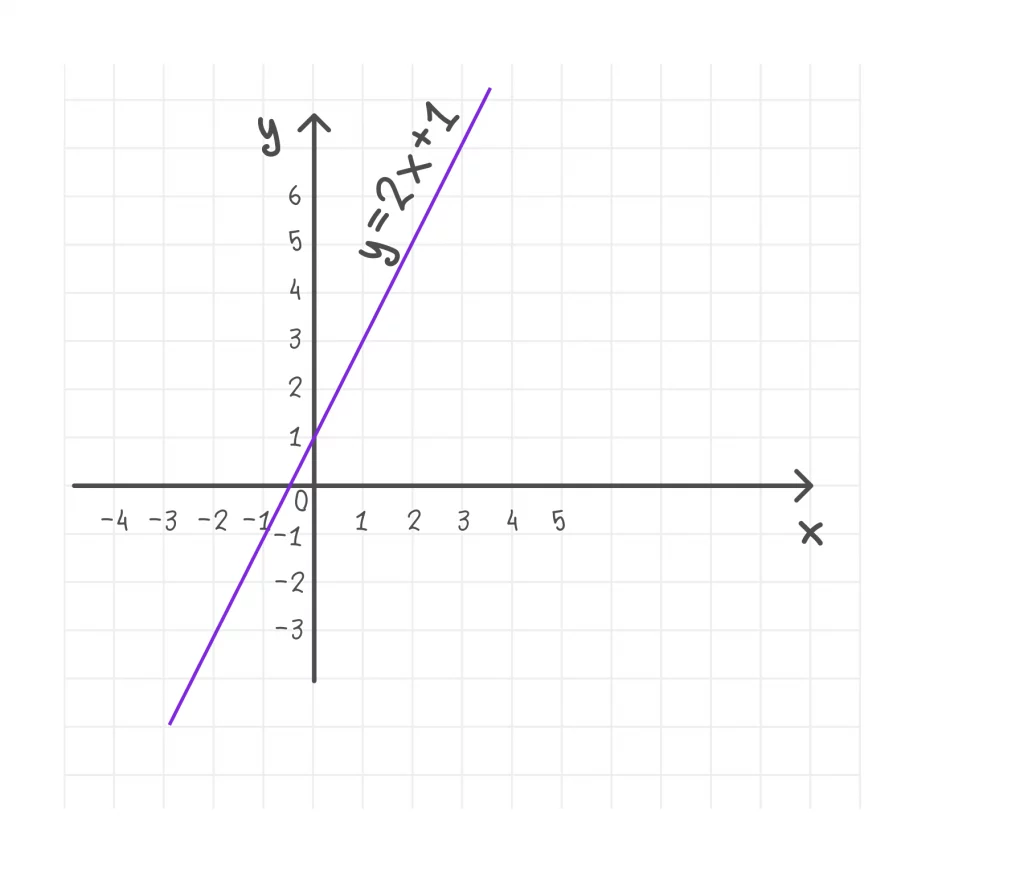
Шаг 4. Проведём прямую через эти точки.

При помощи линейки проведём прямую через отмеченные точки. Полученная прямая  — график функции y = 2x + 1.

👉 Условия параллельности и перпендикулярности двух прямых

Иногда нужно определить, параллельны две прямые или перпендикулярны.

Пусть есть две прямые y =k₁x + b₁ и y = k₂x + b₂.

→ Параллельность

Две прямые параллельны, если их угловые коэффициенты равны:

k₁ = k₂ и при этом b₁ ≠ b₂​

Если b₁ = b₂​, тогда эти две прямые совпадают. И действительно, если k₁ = k₂ и b₁ = b₂​, то получим два одинаковых уравнения прямых.

Рассмотрим это условие на примере.

Пример:
y = 2x + 1 и y = 2x − 3 — параллельные прямые. 

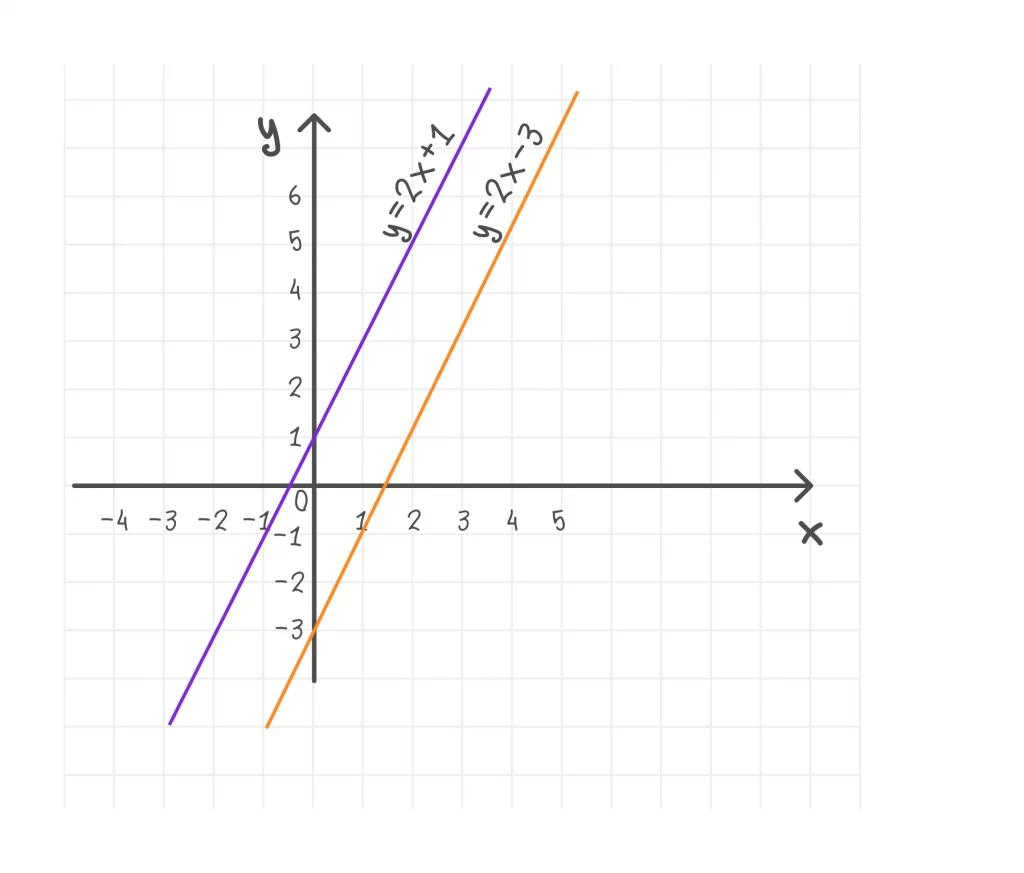
→ Перпендикулярность

Две прямые перпендикулярны, если произведение их угловых коэффициентов равно −1:

k₁⋅k₂ = −1

Пример:
y = x + 1 и y = −x + 4  — перпендикулярные прямые, потому что 1⋅(−1​) = −1. 

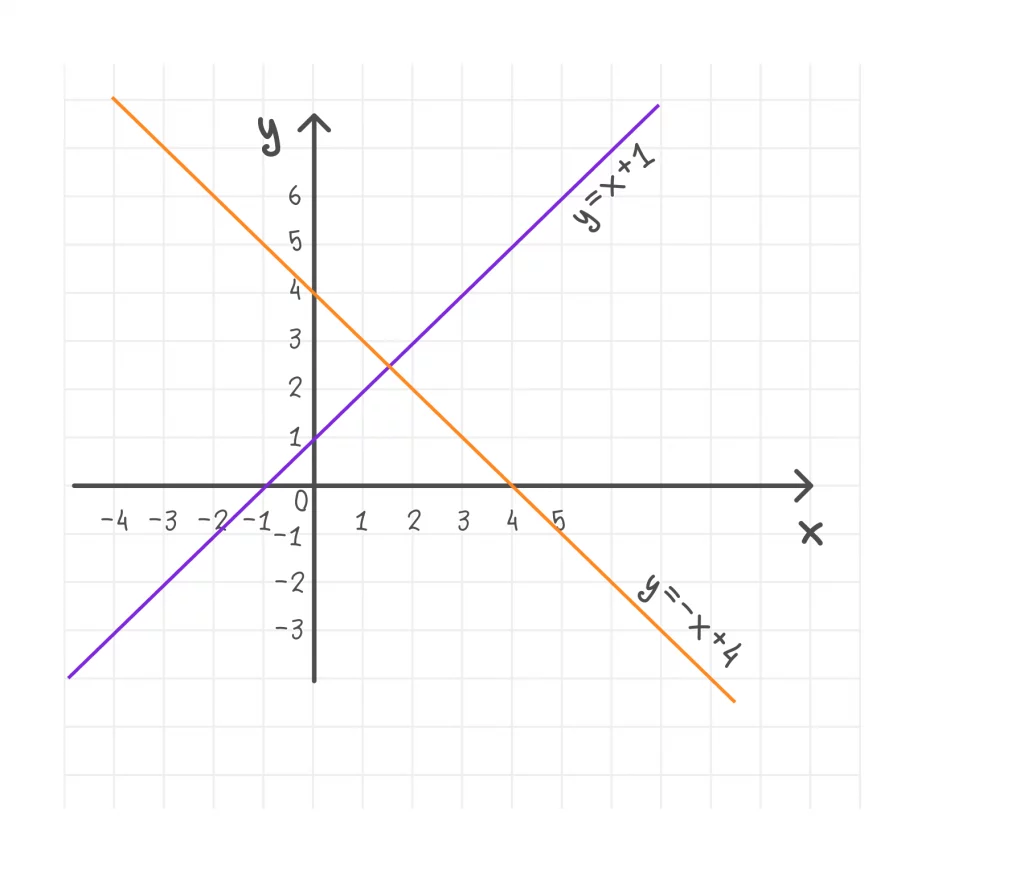
Свойства линейной функции

1️⃣ Область определения линейной функции — множество всех действительных чисел.

2️⃣ Множество значений линейной функции — множество всех действительных чисел.

3️⃣ График линейной функции — прямая.

4️⃣ Функция не имеет ни наибольшего, ни наименьшего значений.

5️⃣ График функции пересекает оси координат:

1. ось абсцисс ОХ — в точке (−b/k; 0): если график пересекает ось ОХ, значит в точке пересечения координата у = 0, тогда получаем: 0 = kx + b, следовательно kx = -b и следовательно x = -b/k (Рисунок 4);
2. ось ординат OY — в точке (0; b): если график пересекает ось OY, значит в точке пересечения координата х = 0, и тогда получаем, что y = k⋅0 + b, а значит y = b (Рисунок 4).

6️⃣ Если b = 0 и k = 0, то функция y = 0, при любом значении аргумента х.

Если b ≠ 0 и k = 0, то функция y = b, при любом значении аргумента х.

А если k ≠ 0 ,  то x = −b/k — является нулём функции.

7️⃣ Функция возрастает на всей области определения при k > 0 и убывает при k < 0.

8️⃣ При k > 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k < 0 функция принимает отрицательные значения на промежутке (−b/k; +∞) и положительные значения на промежутке (−∞; −b/k).

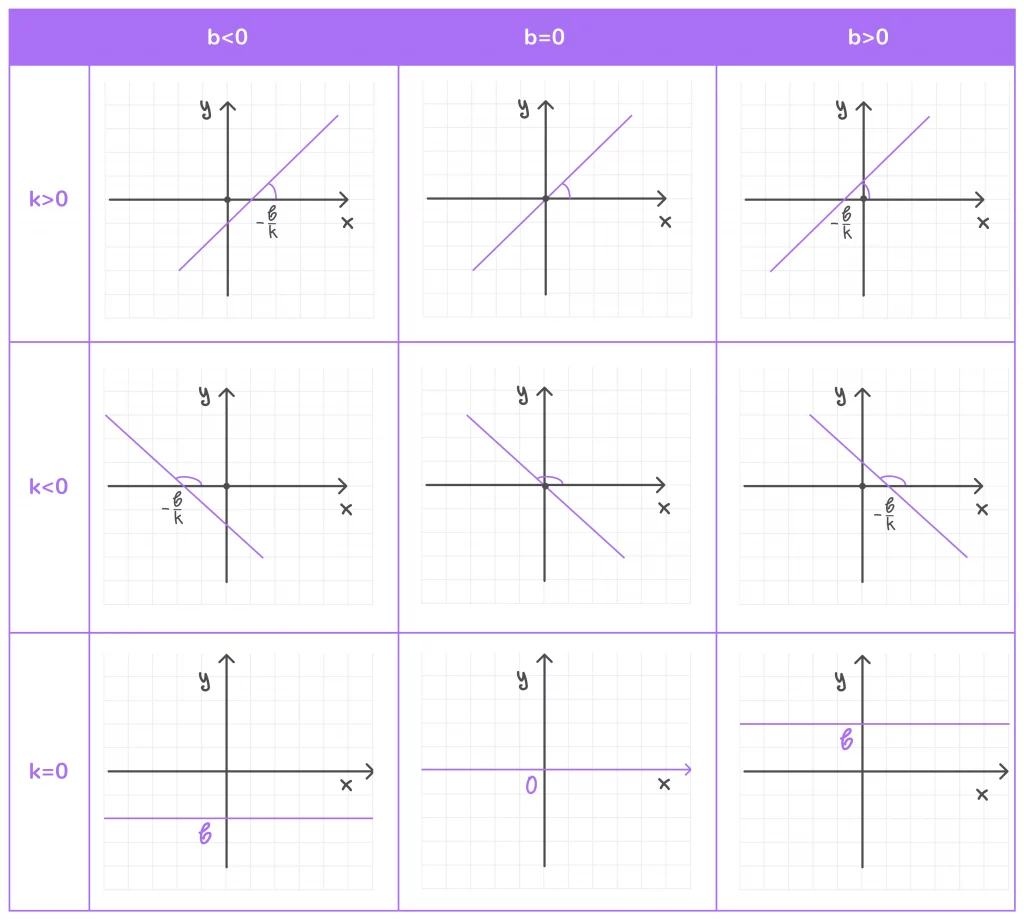
9️⃣ Коэффициент k определяет угол между прямой (графиком функции) и положительным направлением оси OX. Коэффициент k называют ещё угловым коэффициентом (Рисунок 4):

1. если k > 0, то этот угол острый;
2. если k < 0 — тупой;
3. а если k = 0, то прямая параллельна оси OX.

Частные случаи линейной функции:

→ Если b = 0, то функция принимает вид y = kx. Такая функция имеет название — прямая пропорциональность. График прямой пропорциональности — прямая,  проходящая через начало координат.

→ Если k = 0, то функция принимает вид y = b. Её график — прямая, параллельная оси OX и проходящая через точку (0; b).

Решение задач на линейную функцию

Рассмотрим теорию на практике.

Задача

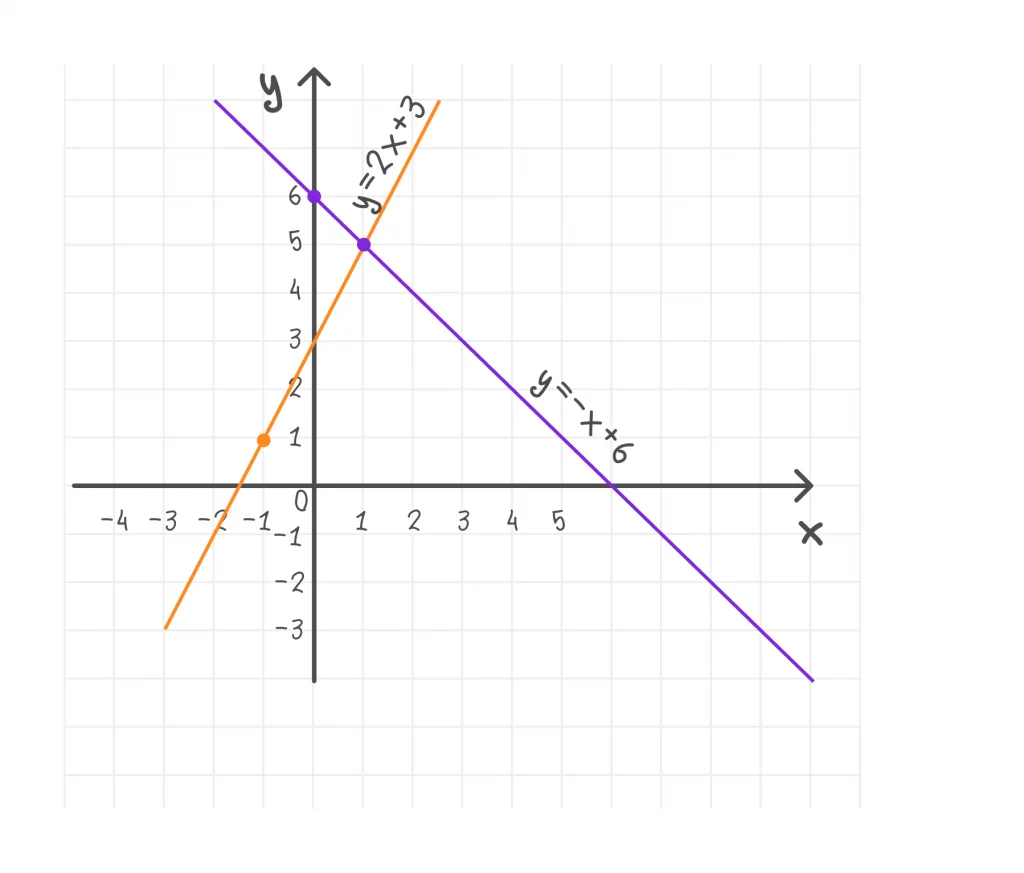
Найдите точку пересечения графиков функций y = 2x + 3 и y = −x + 6. Постройте графики.

Решение:

1. Чтобы найти точку пересечения, приравняем правые части:
2x + 3 = −x + 6

Решим уравнение:
3x = 3 ⇒ x = 1

Подставим x = 1 в любую из функций и найдём у:
y = 2⋅(1) + 3 = 5.

Прямые  пересекаются в точке (1; 5).

2. Построим графики.

а) y = 2x + 3.

1. k = 2, b = 3;
2. найденная в п.1. точка (1; 5) принадлежит графику функции y = 2x + 3;
3. найдём координаты ещё одной точки графика этой функции: пусть х = -1, тогда у = 2⋅(-1) + 3 = 1; получили точку (-1; 1)

b) y = −x + 6.

1. k = -1, b = 6;
2. найденная в п.1. точка (1; 5) принадлежит графику функции y = −x + 6;
3. найдём координаты ещё одной точки графика данной функции: пусть х = 0, тогда у = 0 + 6 = 6;
4. получили точку (0; 6).

Отметим точки на координатной плоскости и построим графики функций (Рисунок 5).

📝Упражнение для самопроверки

Попробуйте следующее задание выполнить самостоятельно.

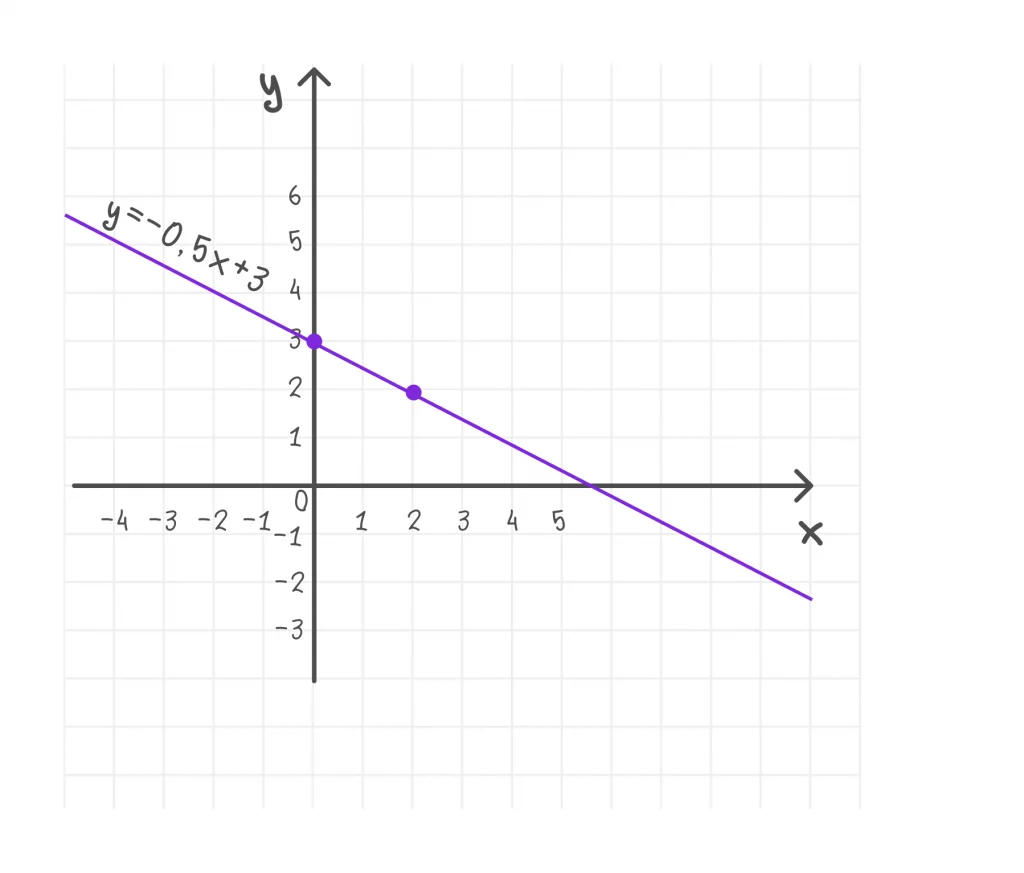
Упражнение. Постройте график функции y = −0,5x + 3 .

Решение: 

Это линейная функция, её график — прямая линия. Уравнение имеет вид y = kx + b, где k = −0,5 — угловой коэффициент (показывает угол наклона прямой), b = 3 — точка пересечения с осью ОУ.

Найдём две точки

Достаточно двух точек, чтобы построить прямую:

1. если х = 0, то у = 3;
2. если х = 2, то у = 2.

Построим график на координатной плоскости

1. Отметим точку (0; 3) — график пересекает ось OY в этой точке.
2. Отметим точку (2; 2).
3. Проведём через эти точки прямую линию — это и есть график функции (Рисунок 6).

Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы. Первый урок — бесплатный ⤵