Формулы приведения

Формулы приведения — это важный инструмент в тригонометрии, который позволяет упростить вычисления и преобразования тригонометрических функций. Эти формулы помогают связать значения тригонометрических функций для углов, выраженных через опорные точки тригонометрической окружности:

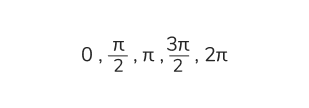
Для учеников 10-го класса, готовящихся к экзаменам или изучающих тригонометрию, формулы приведения являются фундаментальным разделом математики. Они занимают второе место по важности после основного тригонометрического тождества и часто используются при решении задач. В статье разберём список формул, их доказательства, способы запоминания и примеры решения задач.

Список формул приведения 

Формулы приведения позволяют выразить значения тригонометрических функций для углов, выраженных через опорные точки тригонометрической окружности. Вот основные формулы ⤵

— Опорная точка π/2:

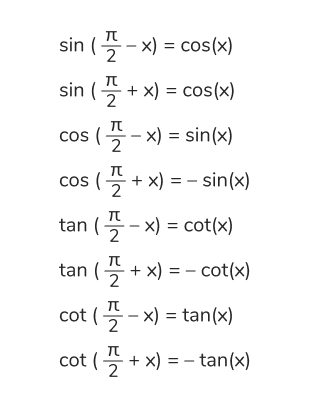
— Oпорная точка π:

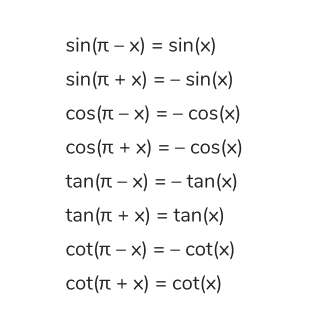
— Oпорная точка 3π/2:

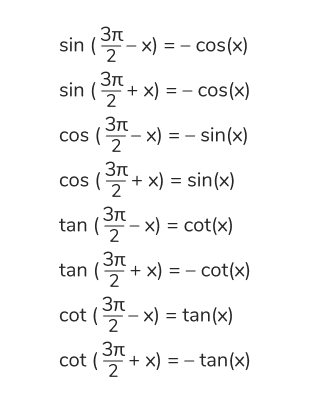
— Опорная точка 2π:

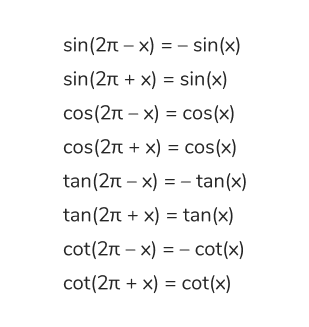
Доказательство формул приведения

Рассмотрим несколько примеров доказательств для лучшего понимания:

📌 Пример 1

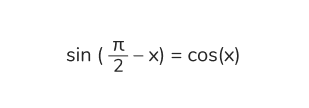
Используем формулу сложения для синуса:

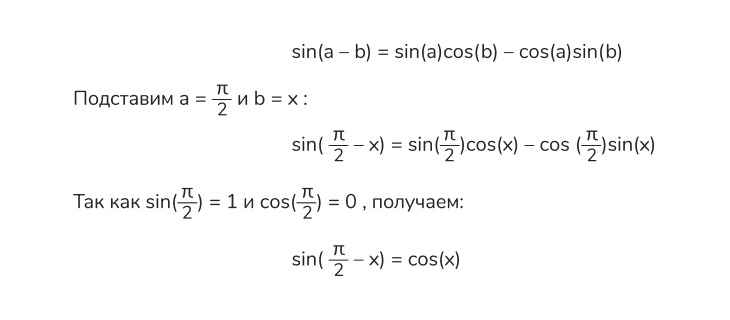
📌 Пример 2

cos(π − x) = −cos(x)

Используем формулу сложения для косинуса:

1. cos(π − x) = −cos(x)

Используем формулу сложения для косинуса:

1. cos(a − b) = cos(a)cos(b) + sin(a)sin(b)

Подставим a = π и b = x :

1. cos(π − x) = cos(π)cos(x) + sin(π)sin(x)

Так как cos(π) = −1 и sin(π) = 0 , получаем:

1. cos(π − x) = −cos(x)

Аналогично можно доказать остальные формулы.

Таблица формул приведения

Для удобства использования формул приведения их часто оформляют в виде таблицы.

Как запомнить формулы приведения

Запомнить все формулы приведения может быть сложно, но существует мнемонический алгоритм, который поможет:

1. Определите четверть: найдите, в какой четверти тригонометрической окружности находится угол.

2. Определите знак функции: знак тригонометрической функции зависит от четверти:

1. sin(x) > 0 в I и II четвертях, sin(x) < 0 в III и IV четвертях.
2. cos(x) > 0 в I и IV четвертях, cos(x) < 0 в II и III четвертях.

3. Определите, меняется ли функция:

1. Если угол содержит 3π/2 или π/2, то функция меняется на кофункцию (sin↔cos , tan↔cot).
2. Если угол содержит 0, π или 2π, то функция не меняется.

Решение задач

Задача 1

Упростите выражение sin(3π/2 — x).

Решение:

1. Определяем четверть: угол 3π/2 — x находится в третьей четверти.

2. Определяем знак: sin(x) < 0 — в третьей четверти.

3. Меняем функцию: sin(3π/2 — x) = -cos(x).

Ответ: -cos(x).

Задача 2

Найдите значение выражения cos(π + π/6).

Решение:

1. Угол π + π/6 находится в третьей четверти.

2. Знак cos(x) < 0 — в третьей четверти.

3. Функция не меняется: cos(π + π/6) = -cos(π/6).

4. Подставляем значение: -cos(π/6) = -√3/2.

Ответ: -√3/2.

Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы!