Формулы сокращённого умножения

В курсе алгебры с 7 по 10 класс учащиеся начинают изучать формулы сокращённого умножения, которые облегчают работу с многочленами и упрощают процесс решения уравнений. Эти формулы помогают представить произведение алгебраических выражений в компактной форме и являются важным инструментом в математике. В статье рассмотрим все формулы, а также их использование на практике.

Основные формулы сокращённого умножения

✔ Квадрат суммы

Формула: 

Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого и второго числа плюс квадрат второго числа.

✔ Квадрат разности

Формула: 

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого и второго числа плюс квадрат второго числа.

✔ Разность квадратов

Формула: 

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность.

✔ Куб суммы

Формула: 

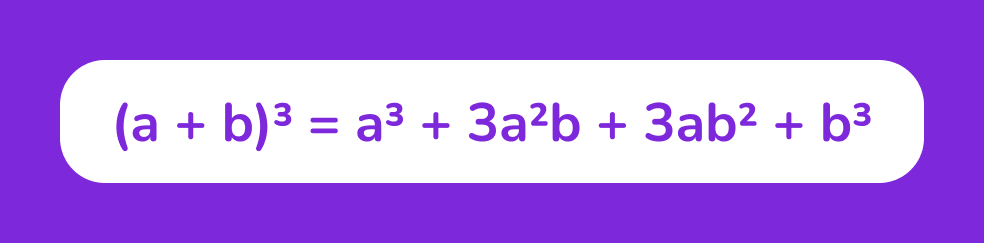
Куб суммы двух чисел равен кубу первого числа плюс тройное произведение квадрата первого числа на второе плюс тройное произведение первого числа на квадрат второго плюс куб второго числа.

✔ Куб разности

Формула: 

Куб разности двух чисел равен кубу первого числа минус тройное произведение квадрата первого числа на второе плюс тройное произведение первого числа на квадрат второго минус куб второго числа.

✔ Сумма кубов

Формула: 

Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат разности этих чисел.

✔ Разность кубов

Формула: 

Разность кубов двух чисел равна произведению разности этих чисел на неполный квадрат суммы этих чисел.

Доказательство формул сокращённого умножения

1. Квадрат суммы

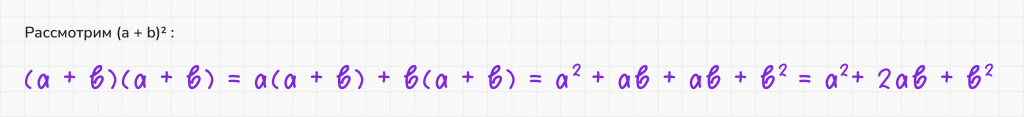
2. Квадрат разности

3. Разность квадратов

4. Куб суммы

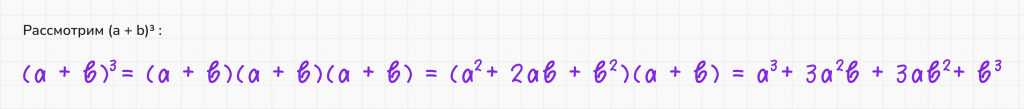
5. Куб разности

6. Сумма кубов

7. Разность кубов

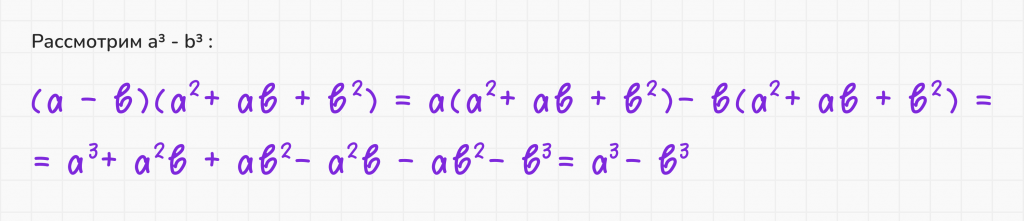
Дополнительные формулы сокращённого умножения

▶ Бином Ньютона

Формула: 

Пример вычисления биномиальных коэффициентов:

▶ Формула возведения в квадрат суммы трёх и четырёх слагаемых

Для трёх слагаемых:

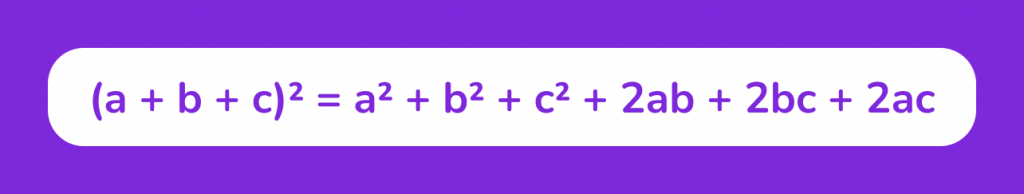
Для четырёх слагаемых:

▶ Формула разности n-ых степеней двух слагаемых

Формула: 

Решение задач на формулы сокращённого умножения

1. Найдите значение выражения:

Решение:

2. Разложите многочлен на множители:

Решение:

3. Найдите значение выражения:

Решение:

Советы по запоминанию формул

1. Используйте ассоциации: связывайте формулы с известными вам понятиями или визуальными образами.
2. Повторяйте регулярно: систематическое повторение помогает лучше запомнить формулы.
3. Решайте больше задач: практика помогает понять и запомнить формулы легче и быстрее.
4. Используйте карточки: создайте карточки с формулами и периодически повторяйте их.

Формулы сокращённого умножения — это важный инструмент в алгебре для упрощения вычислений и решения задач. Их понимание и умение применять значительно облегчают работу с многочленами, а также выражениями в средних и старших классах школы.

Если ребёнок испытывает трудности в работе с формулами сокращённого умножения, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия 💜