Как найти диаметр окружности: формулы 

В 6-м классе школьной программы ученики начинают знакомиться с окружностью  и кругом. В мире математики окружность и круг — это фундаментальные фигуры, которые встречаются в повседневной жизни и различных областях науки. Для эффективной работы с этими фигурами важно понимать, как найти диаметр окружности и знать связанные с ним формулы. В этой статье мы рассмотрим основные понятия, формулы и методы нахождения диаметра окружности.

Основные понятия

Прежде чем перейти к расчётам, разберёмся с основными терминами, связанными с окружностью и кругом.

1. Круг

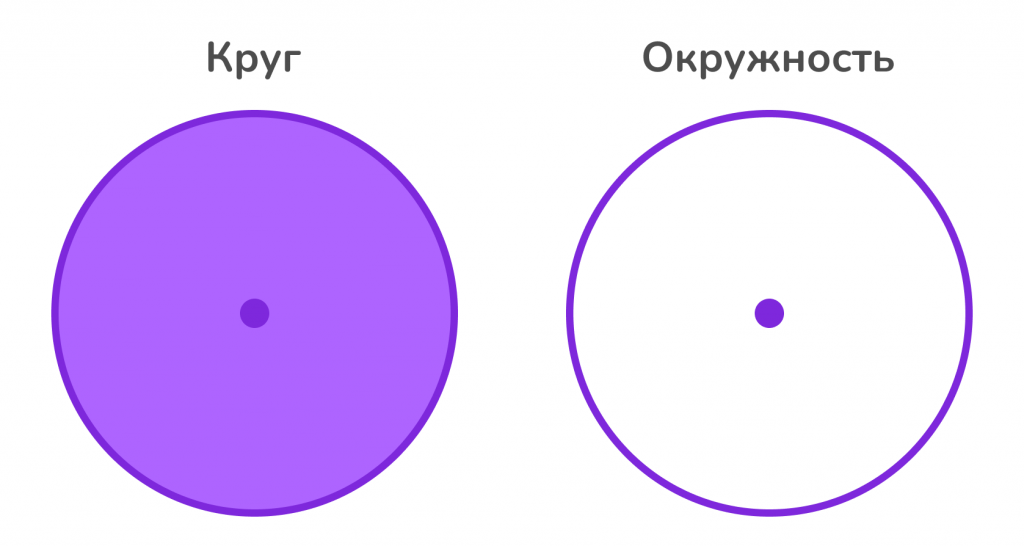
Круг — это геометрическая фигура, состоящая из всех точек плоскости, которые находятся на расстоянии, не превышающем заданное, от одной фиксированной точки, называемой центром круга.

2. Окружность

Oкружность — это замкнутая кривая, состоящая из всех точек плоскости, находящихся на фиксированном расстоянии (радиусе) от центра. Окружность является границей круга.

3. Радиус

Pадиус (обозначается как r) — это расстояние от центра круга до любой точки на его окружности. Радиус является половиной диаметра.

4. Диаметр

Диаметр (обозначается как d) — это отрезок, проходящий через центр круга и соединяющий две точки на окружности. Он в два раза длиннее радиуса (d = 2r).

5. Длина окружности

Длина окружности (обозначается как L) — это расстояние вокруг окружности. Она вычисляется по формуле:

L = 2πr = 2d, где π ≈ 3.14159.

Формулы диаметра окружности

Существует несколько способов нахождения диаметра окружности в зависимости от доступной информации.

➤ Общая формула через радиус окружности

Если известен радиус окружности, диаметр можно найти по следующей формуле:

d = 2r, где r — радиус окружности.

Пример. Если радиус окружности равен 5 см, диаметр будет: d = 2 ∙ 5 = 10 см.

➤ Формула через длину окружности

Если известна длина окружности, диаметр можно найти с помощью формулы:

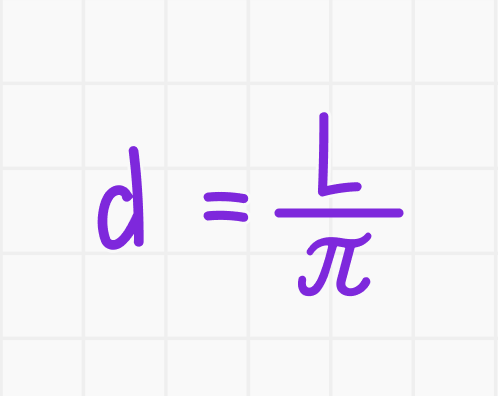
где L — длина окружности, а π — константа.

Пример. Если длина окружности равна 31.4 см, диаметр можно найти так:

Нахождение диаметра окружности по чертежу

На чертеже диаметр окружности может быть обозначен как прямая линия, проходящая через центр окружности. Для нахождения диаметра можно использовать линейку или измерительный инструмент.

Если на чертеже диaметр окружности измерён как 6 см, значит, диaметр окружности равен 6 см.

Решение задач на нахождение диаметра окружности

Рассмотрим несколько задач на нахождение диаметра окружности.

Задача 1. Pадиус окружности равен 12 см. Найдите диaметр окружности.

Решение. Используем формулу:

d = 2r.

Подставляем значение радиуса:

d = 2 ∙ 12 = 24 см.

Ответ: диаметр окружности равен 24 см.

Задача 2. Длина окружности равна 50 см. Найдите диaметр окружности.

Решение. Используем формулу:

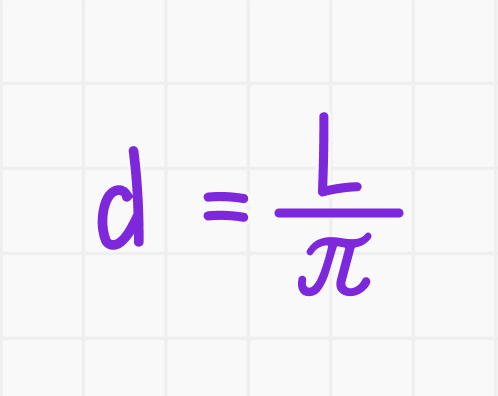
Подставляем значение длины окружности:

Ответ: диaметр окружности примерно равен 15,92 см.

Задача 3. Диаметр окружности равен 8 см. Найдите радиус окружности.

Решение. Используем формулу:

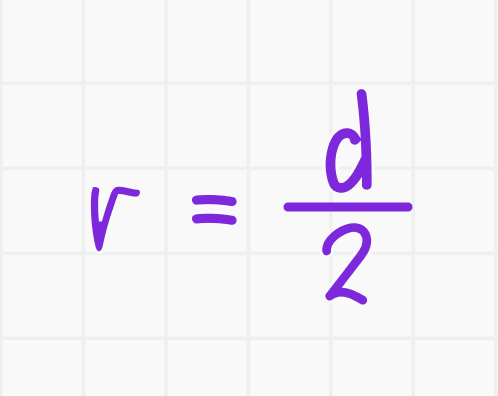
Подставляем значение диаметра:

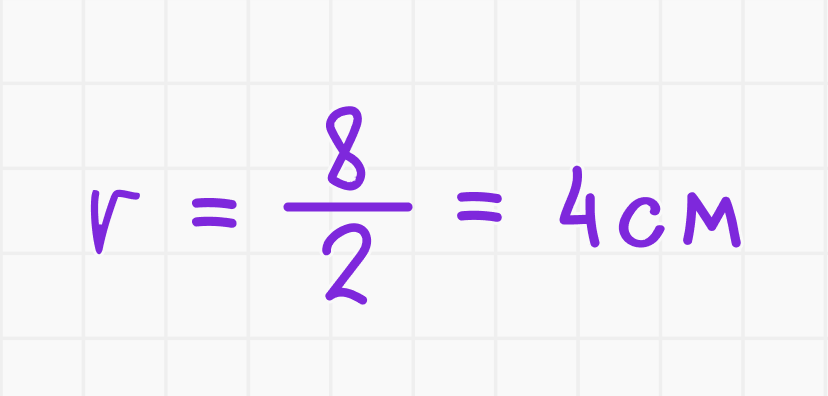
Ответ: радиус окружности равен 4 см.

Задача 4. На чертеже длина диаметра окружности измерена как 14 см. Найдите радиус окружности.

Решение. Используем формулу:

Подставляем значение диаметра:

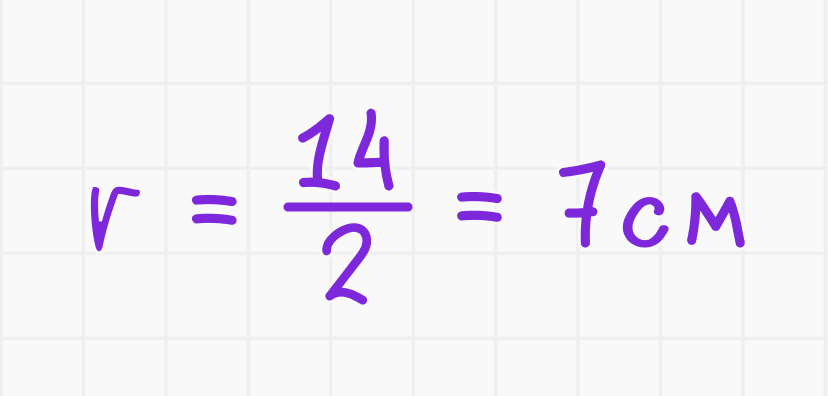
Ответ: радиус окружности равен 7 см.

Задача 5. Pадиус окружности равен 10 см. Какова длина окружности?

Решение. Используем формулу:

L = π ∙ d.

Сначала находим диaметр:

d = 2r = 2 ∙ 10 = 20 см.

Теперь находим длину окружности:

L = π ∙ 20 ≈ 3,14 ∙ 20 = 62,8 см.

Ответ: длина окружности равна 62,8 см.

Задача 6. Длина окружности составляет 31.4 см. Найдите радиус окружности.

Решение. Сначала найдём диaметр:

Теперь найдём радиус:

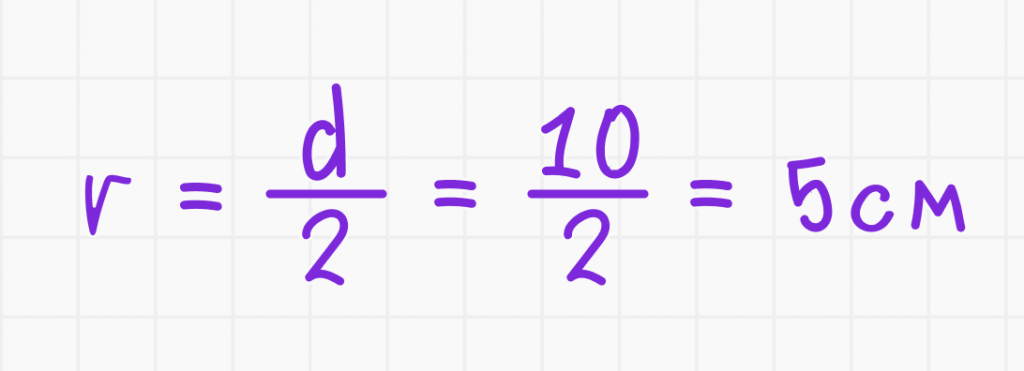
Ответ: радиус окружности равен 5 см.

---

Диаметр — это важный элемент при работе с окружностями. Понимание, как находить диаметр по радиусу, длине окружности или на чертеже, позволяет решать разнообразные задачи и использовать эти знания в практических ситуациях. 

Если ребёнок испытывает трудности при нахождении диаметра окружности, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия 💜