Чётные и нечётные числа

Знаменитый Пифагор более 2 тысяч лет назад впервые разделил числа на чётные и нечётные. Школьники же знакомятся с понятием чётности во втором классе, когда начинают изучение умножения и деления. Зачем необходимо знать, какие числа называются чётными? Разве недостаточно просто выучить таблицу умножения?

В статье мы найдём ответы на эти вопросы, узнаем, как определить чётность многозначных чисел, а также научимся использовать свойства чётных чисел при выполнении арифметических действий. 

Числа, которые называются чётными

Число, которое делится на два без остатка, называется чётным. Например, 6 — чётное число, потому что 6 : 2 = 3 

Чтобы определить чётное число, необязательно каждый раз производить вычисления. Достаточно запомнить правило: все числа, которые оканчиваются на цифры 0, 2, 4, 6 или 8, являются чётными.

Зная это правило, каждый сможет легко определить чётность любого многозначного числа. Давайте проверим. Число 65 498 (шестьдесят пять тысяч четыреста девяносто восемь) чётное или нечётное? 

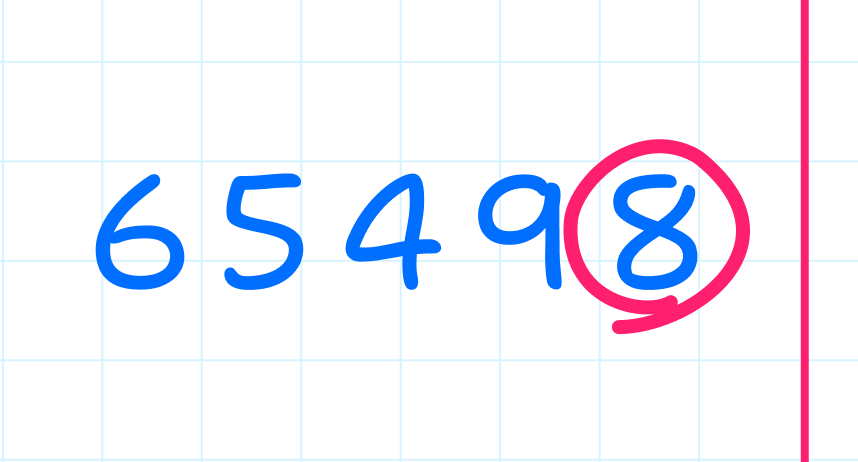
Какие числа называются нечётными

Нечётные числа — те, что не делятся на два без остатка. Например, 9 — число нечётное, потому что 9 : 2 = 4 (ост.1) 

Интересно, что при делении любого нечётного числа на 2, остаток всегда равен единице. 

Определить нечётное число можно также по последней цифре в его записи. Если число оканчивается на 1, 3, 5, 7 или 9, то оно нечётное.

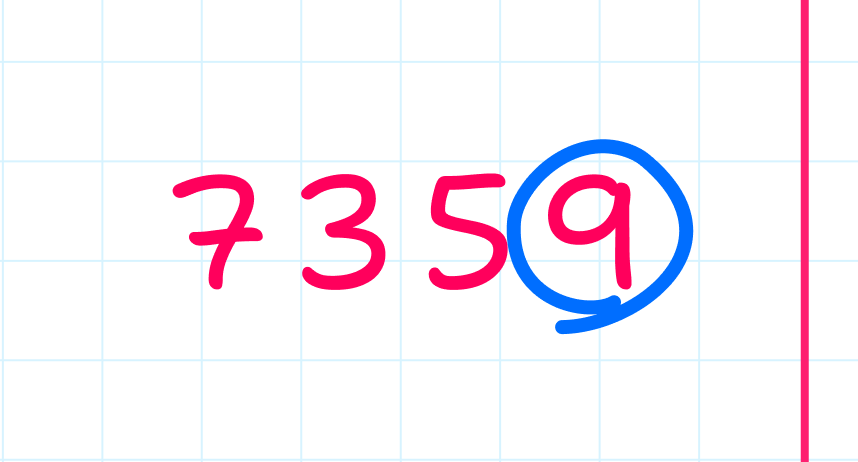
Чётные числа и счёт

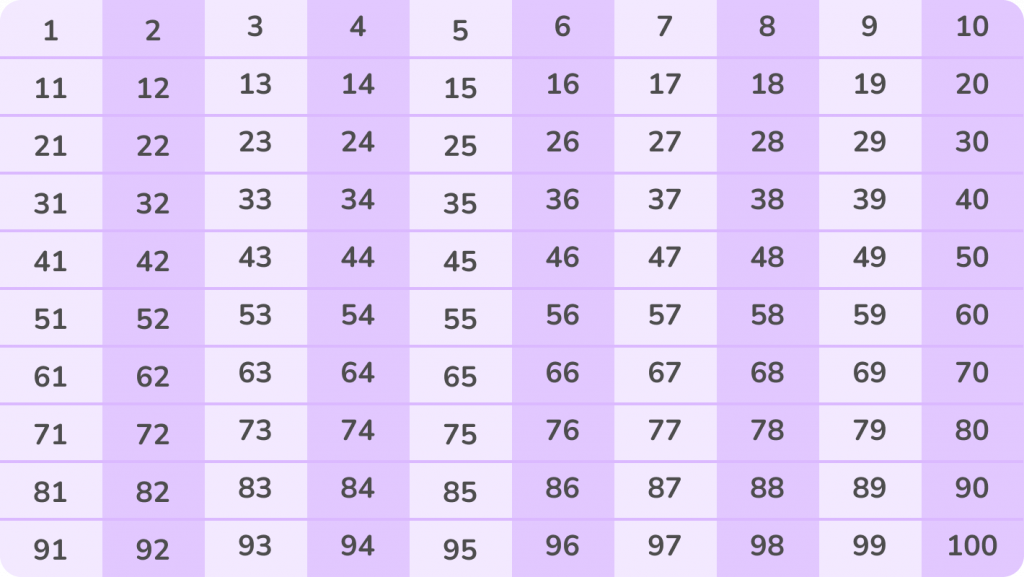
При счёте чётные числа чередуются с нечётными. Это наглядно видно на рисунке. 

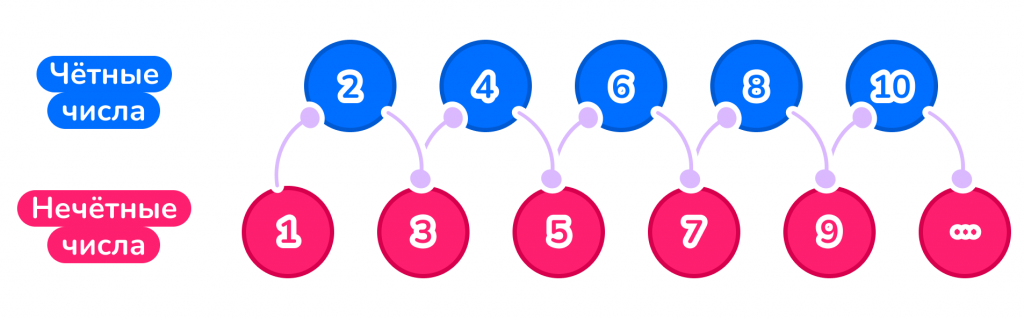
Так, любое чётное число всегда стоит в окружении двух нечётных и наоборот. Например, число 23 — нечётное. Его соседи 22 и 24 — чётные. 

Но вот интересный вопрос: 0 — это чётное или нечётное число? Ответить на него нам помогут изученные ранее правила:

1. Мы уже знаем, что числа при счёте чередуются, значит 0, который стоит перед нечётной единицей, является чётным числом. 
2. Числа, которые оканчиваются на 0, чётные. Пусть 0 — однозначное число, это правило также применимо. 
3. И самое важное, ноль делится на два без остатка. Значит ноль — чётное число. 

Свойства чётных чисел

1. Сумма чётных чисел является чётным числом

Чётное число + чётное число = чётное число:

6 + 8 = 14 (14 : 2 = 7; 14 — чётное число).

Чётное число + чётное число + чётное число = чётное число:

22 + 6 + 10 = 38 (38 : 2 = 19; 38 — чётное число).

2. Два нечётных числа — это чётное число

Нечётное число + нечётное число = чётное число:

7 + 9 = 16 (16 : 2 = 8; 16 — чётное число). 

3. Сумма чётного и нечётного числа — это нечётное число

Нечётное число + чётное число = нечётное число:

11  + 10 = 21 (21 : 2 = 10 (остаток 1); 21 — нечётное число).

Чётное число + нечётное число = нечётное число:

8 + 23 = 31 (31 : 2 = 15 (остаток 1); 31 — нечётное число).

4. Разность двух нечётных чисел является чётным числом

Нечётное число — нечётное число = чётное число:

17 — 3 = 14 (14 : 2 = 7; 14 — чётное число) 

5. Разность двух чётных чисел — чётное число

Чётное число — чётное число = чётное число:

22 — 10 = 12 (12 : 2 = 6; 6 — чётное число).

6. Произведение двух чётных чисел является чётным числом

Чётное число * чётное число = чётное число:

6 * 6 = 36 (36 : 2 = 18; 36 — чётное число).

7. Произведение двух нечётных чисел — нечётное число

Нечётное число * нечётное число = нечётное число:

5 * 5 = 25  (25 : 2 = 14 (остаток 1); 25 — нечётное число).

8. Если чётное число умножить на нечётное, то получится чётное число

Нечётное число * чётное число = чётное число:

3 * 8 = 24 (24 : 2 = 12; 24 — чётное число).

Чётное число * нечётное число = чётное число:

4 * 5 = 20 (20 : 2 = 10; 20 — чётное число).

Знание этих свойств поможет быстро решать примеры и применять устные приёмы вычислений по теме чётные и нечётные числа.

Практические задания

Выполните несколько заданий и потренируйтесь в определении чётности чисел. 

Задание 1. Запишите нечётные числа в порядке возрастания и разгадайте слово. 

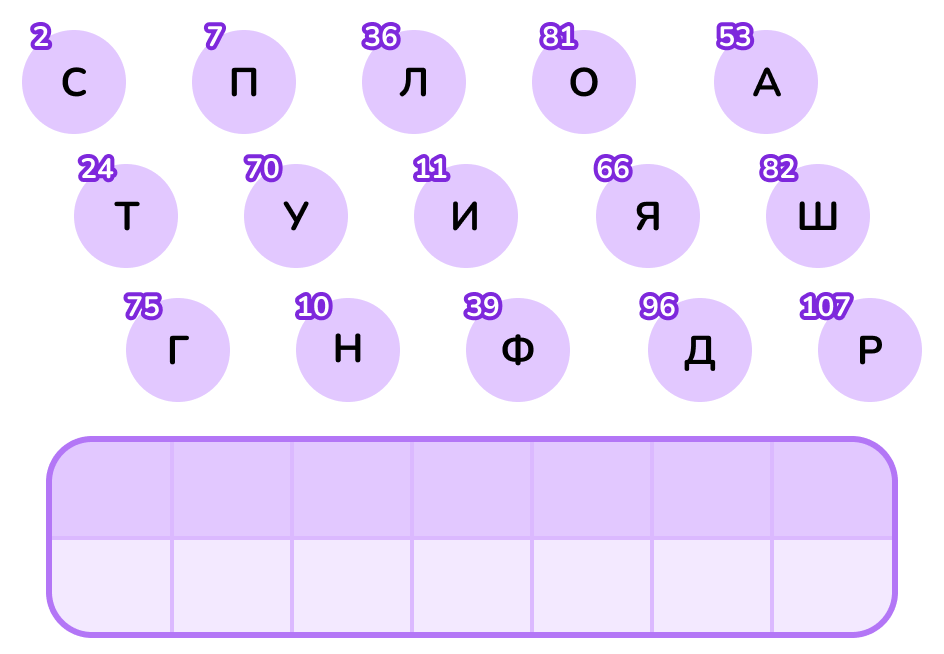
Проверьте себя:

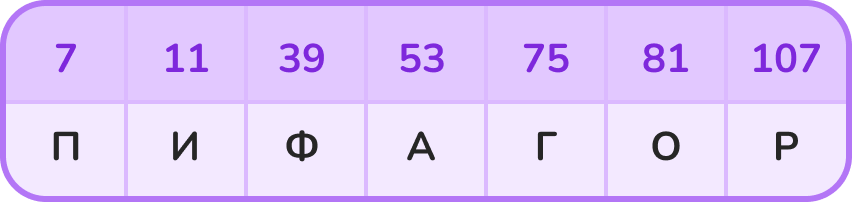
Задание 2. Запишите все чётные числа, расположенные между числами 40 и 50. А затем запишите нечётные числа, расположенные между 21 и 41. 

 Проверьте себя: 

1) 42, 44, 46, 48.

2) 23, 25, 27, 29, 31, 33, 35, 37, 39. 

Задание 3. Выполните вычисления и определите, чётное или нечётное получилось число.

Проверьте себя: 

Задание 4. Алиса загадала чётное число, разделила его на 2, прибавила 13, вычла 4 и получила 12. Какое число загадала Алиса? 

Проверьте себя:

Можно найти ответ, решив уравнение: 

x : 2 + 13 — 4 = 12 

х : 2 = 12 + 4 — 13

x : 2 = 3

x = 2 * 3 

х = 6  — чётное число

Задание 5. Запишите все нечётные двузначные числа, оканчивающиеся на цифру 3. Найдите их сумму. Какое получилось число: чётное или нечётное? 

Проверьте себя:

1) 13 + 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 = 477.

2) 477 заканчивается на цифру 7, значит число нечётное. 

Известное с древних времён понятие чётности встречается нам не только в вычислениях, но и в повседневной жизни. Знание свойств и понятий, связанных с определением чётности числа, позволит подмечать закономерности и накапливать опыт работы с числами, способствуя тем самым улучшению вычислительных навыков.

Важно запомнить по теме чётные и нечётные числа следующее: 

1. если число оканчивается на 0, 2, 4, 6 или 8, то оно чётное;
2. четные и нечётные числа при счёте чередуются;
3. 0 — чётное число;
4. при сложении, умножении и вычитании двух чётных чисел, получается чётное число. 

Если нужна помощь в отработке темы, приходите на наши онлайн-занятия по математике. Будем рады вам и вашему школьнику 💜