Умножение десятичных дробей

В повседневной жизни мы часто сталкиваемся с числами, содержащими дробную часть: цена товара, масса упаковки, длина детали, время. Все эти числа удобнее записывать в виде десятичных дробей. Чтобы уметь решать задачи и проводить вычисления, нужно знать, как правильно работать с такими дробями. В этой статье мы разберём, что такое десятичная дробь и как их умножать.

Понятие десятичной дроби

Например:

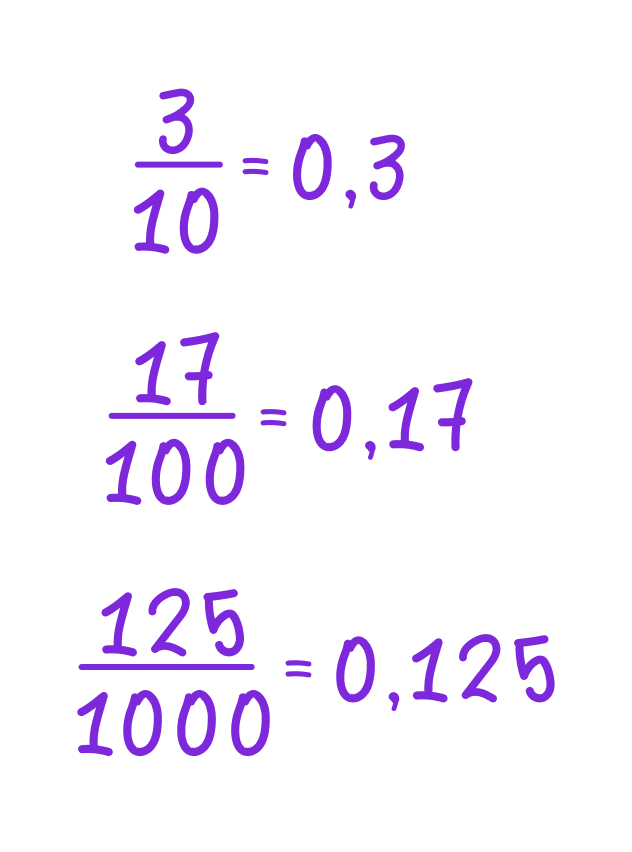
Главная особенность: дробная часть записывается после запятой.

Пример ⤵

Число 0,52 означает 52 сотых, то есть:

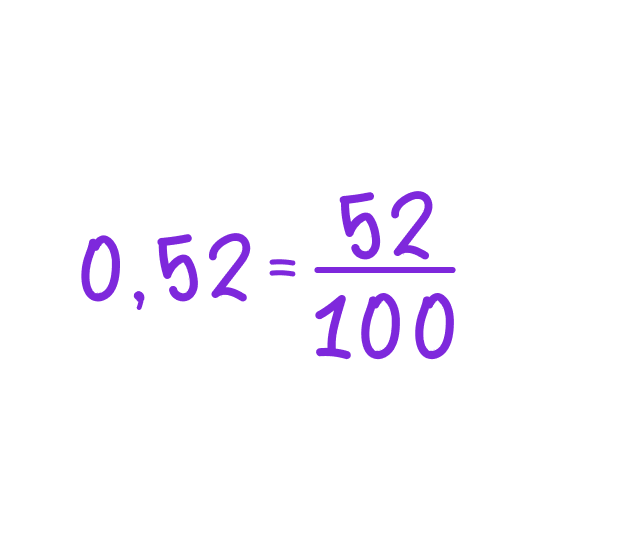
Как записать и правильно читать десятичную дробь

Чтобы записать десятичную дробь, нужно отделить целую часть от дробной с помощью запятой.

Правила чтения:

1. 0,3 — ноль целых три десятых;
2. 2,75 — две целых семьдесят пять сотых;
3. 5,004 — пять целых четыре тысячных.

Примеры перевода ⤵

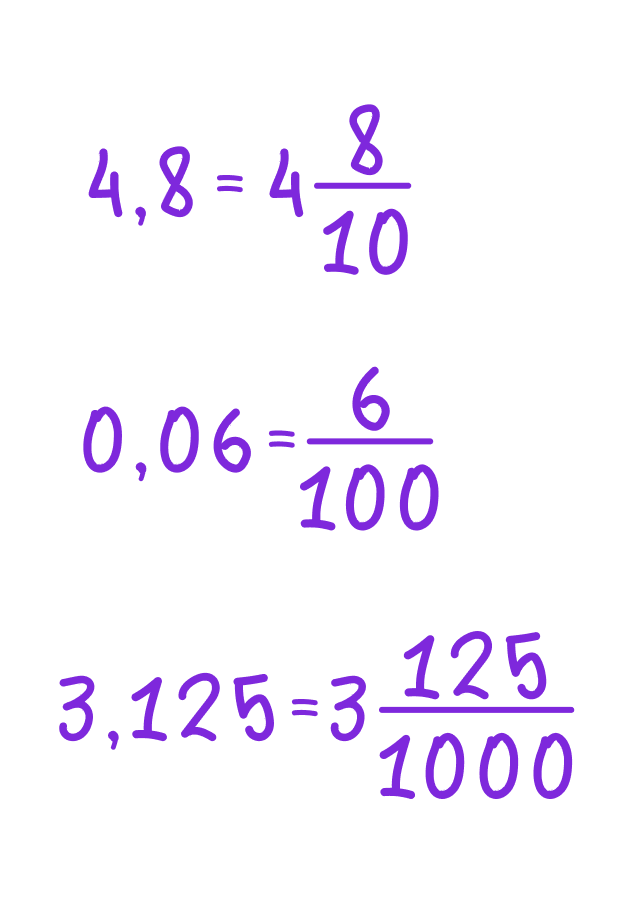
Свойства десятичных дробей

1️⃣ Нули в конце дробной части можно дописывать и убирать.

0,5 = 0,50 = 0,500

2️⃣ «Ширина» дробной части влияет только на точность, а не на значение.

1,4 и 1,40 обозначают одно и то же число.

3️⃣ Если сравнивать две десятичные дроби, их удобно «уравнять по количеству цифр» после запятой.

0,7 и 0,56 → 0,70 и 0,56 → 0,70 > 0,56

Свойства умножения

При работе с десятичными дробями действуют обычные свойства умножения ⤵

Умножение десятичных дробей на натуральное число

Алгоритм ⤵

1. Умножить число без запятой на натуральное число.

2. В результате поставить запятую в том же месте, где она была в дроби.

Пример 1

0,4 ⋅ 3

1. 4 · 3 = 12
2. В 0,4 одна цифра после запятой → 1 цифра после запятой в ответе
3. 0,4⋅3 = 1,2

Пример 2

2,75 ⋅ 4

1. 275 · 4 = 1 100
2. В 2,75 — две цифры после запятой → 2 цифры после запятой в ответе
3. 2,75⋅4 = 11,00 = 11

Умножение десятичных дробей в столбик

Алгоритм ⤵

1. Умножить числа, не обращая внимания на запятые.

2. Посчитать, сколько всего цифр после запятой было в обоих множителях.

3. Поставить запятую в ответе, отсчитав полученное количество цифр справа налево.

Пример:

1,2⋅0,35

Шаг 1: умножаем 12 × 35 = 420.
Шaг 2: цифр после запятой: в 1,2 — 1; в 0,35 — 2 → всего 3.
Шаг 3: ставим запятую: 0,420 = 0,42.

Ответ: 1,2⋅0,35 = 0,42

Умножение десятичных дробей на 10, 100, 1000

При умножении на 10, 100, 1000 и т. д. запятая перемещается вправо на столько цифр, сколько нулей.

Примеры:

1. 4,8⋅10 = 48 — запятая сдвинулась на 1 разряд.
2. 0,36⋅100 = 36 — на 2 разряда.
3. 5,07⋅1000 = 5 070 — на 3 разряда.

Умножение десятичных дробей на 0,1; 0,01; 0,001

Эти числа — это 1/10, 1/100, 1/1000.

Поэтому при умножении запятая перемещается влево на количество цифр после запятой в множителе.

Примеры:

1. 7,5⋅0,1 = 0,75 — сдвиг на 1 разряд.
2. 4,2⋅0,01 = 0,042 — на 2 разряда.
3. 3,19⋅0,001 = 0,00319 — на 3 разряда.

Умножение десятичной дроби на обыкновенную дробь

Чтобы умножить десятичную дробь на обыкновенную, нужно:

1. Записать десятичную дробь в виде обыкновенной.

2. Перемножить дроби.

3. Перевести результат обратно в десятичную дробь (если нужно).

Пример 1

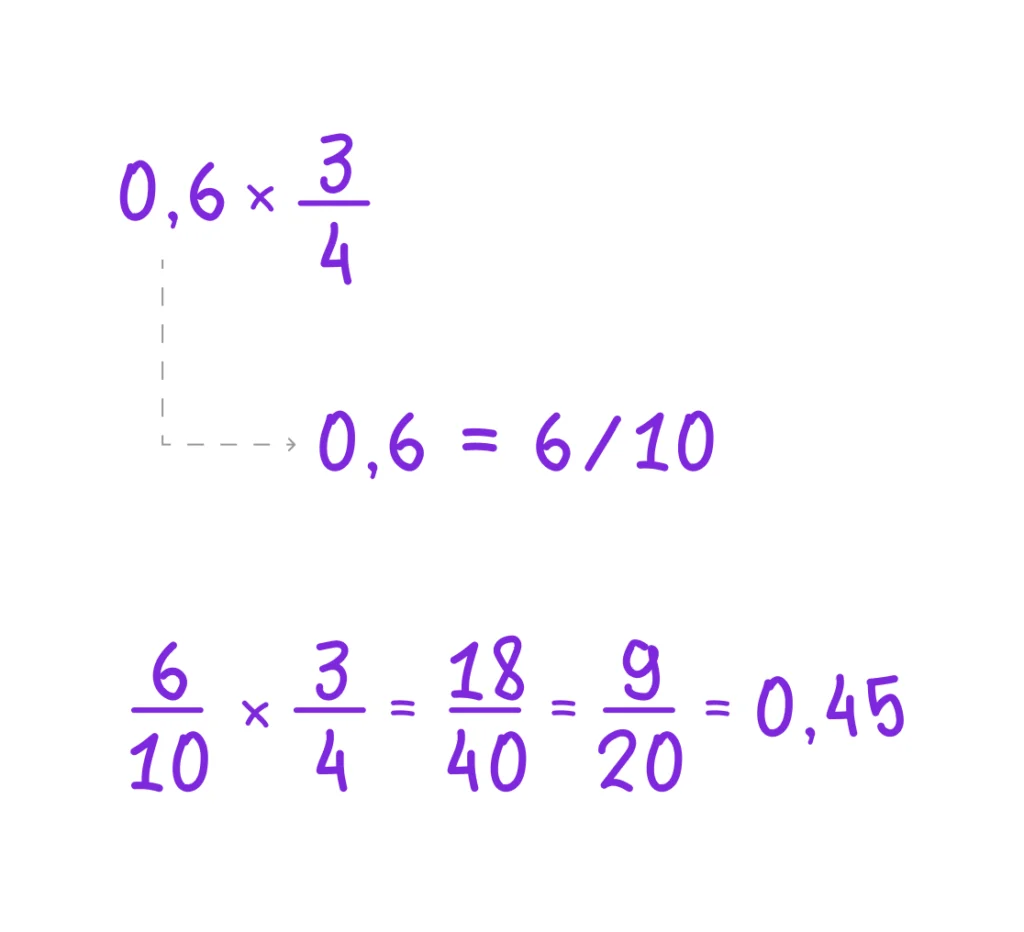
Пример 2

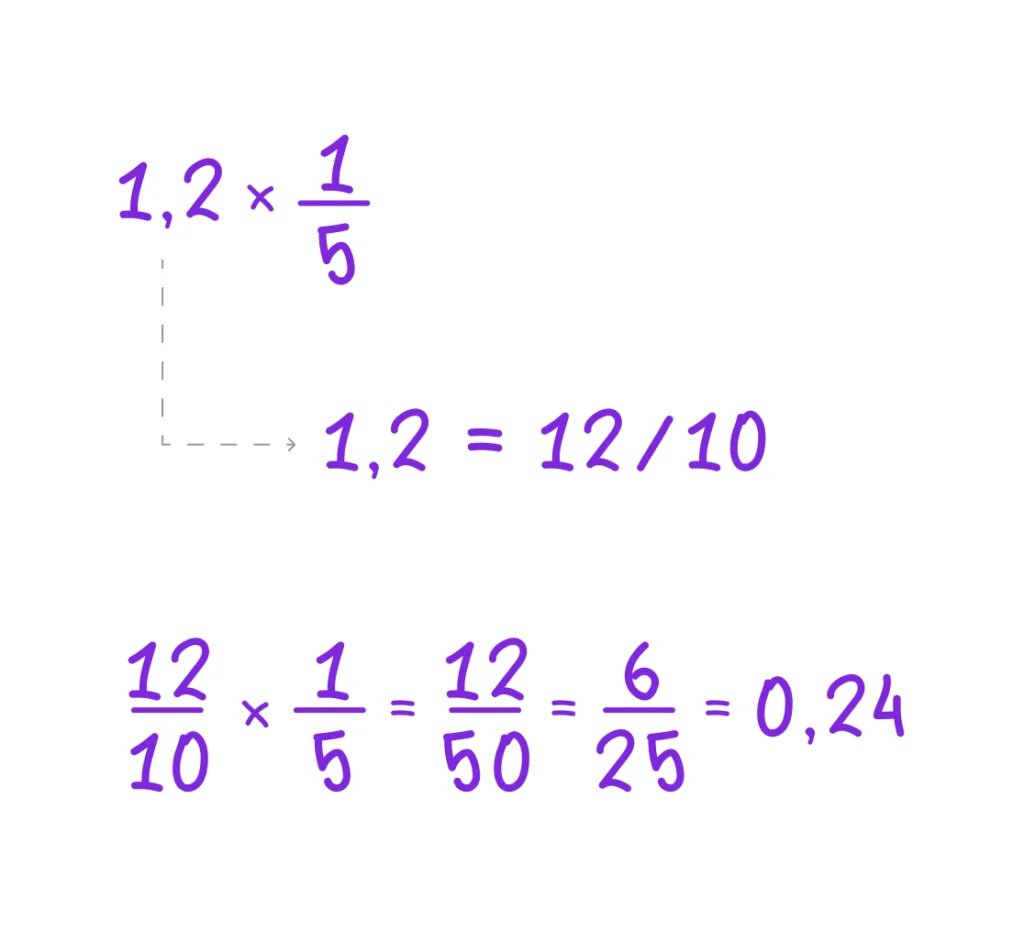
Подведём итоги

Умножение десятичных дробей — важный и полезный навык. Чтобы успешно выполнять такие вычисления, достаточно помнить несколько правил:

1. игнорировать запятые при умножении и обязательно ставить их в конце;
2. правильно считать количество разрядов после запятой;
3. пользоваться свойствами умножения;
4. свободно переводить десятичные дроби в обыкновенные и обратно.