
Треугольник
Треугольник — одна из самых простых, но в то же время важнейших фигур в геометрии. Он встречается повсеместно: от задач на уроках математики до реальных жизненных ситуаций, например, при строительстве или создании различных конструкций.
В 7-9-х классах изучение треугольников становится ключевым этапом в освоении геометрии. Именно здесь ученики знакомятся с основными понятиями: видами треугольников, их элементами (стороны, углы, высоты, медианы и биссектрисы), а также важными теоремами, такими как теорема Пифагора. Эти знания помогают не только решать задачи на уроках, но и развивают логическое мышление, что важно для понимания более сложных тем в старших классах.
В статье подробно рассматриваем основные свойства треугольников: определение, классификация, теорема Пифагора, медианы, биссектрисы, высоты, средняя линия, периметр, площадь, признаки равенства и подобия, а также свойства вписанной и описанной окружностей.

📎 Треугольник: определение и типы
Определение треугольника
Треугольник — это геометрическая фигура, которая состоит из трёх отрезков, соединяющих три точки (вершины), не лежащие на одной прямой. Эти отрезки называются сторонами треугольника, а точки их пересечения — вершинами.
Каждый треугольник имеет три угла, которые образуются при пересечении его сторон. Сумма всех углов треугольника всегда равна 180°.
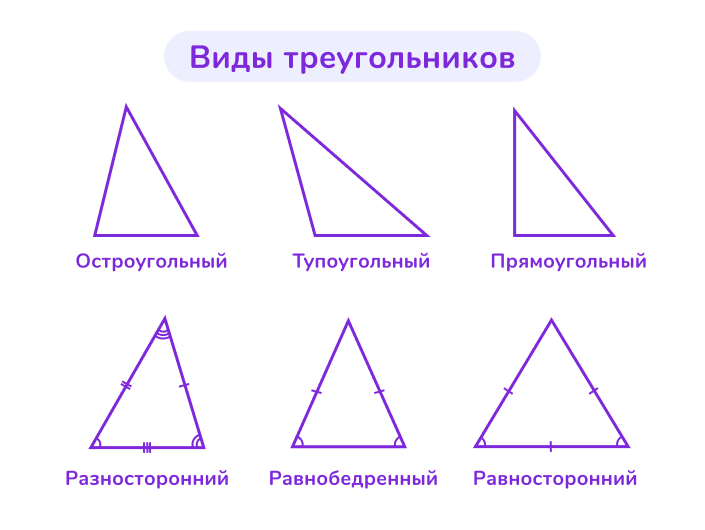
📌 Типы треугольников
1. По углам:
- Остроугольный треугольник: все углы треугольника меньше 90°.
- Прямоугольный треугольник: один из углов равен 90°. Сторона, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны — катетами.
- Тупоугольный треугольник: один из углов больше 90°.
2. По сторонам:
- Разносторонний треугольник: все стороны треугольника имеют разную длину.
- У равнобедренного треугольника: две стороны треугольника равны между собой. Эти стороны называются боковыми сторонами, а третья сторона — основанием. Углы при основании также равны.
- Равносторонний треугольник (правильный треугольник): все три стороны треугольника равны. Все углы такого треугольника равны 60°.
📎 Прямоугольный треугольник и теорема Пифагора
Прямоугольный треугольник — это треугольник, у которого один из углов равен 90°. Стороны прямоугольного треугольника имеют специальные названия:
- Катеты — две стороны, которые образуют прямой угол.
- Гипотенуза — сторона, лежащая напротив прямого угла. Гипотенуза всегда является самой длинной стороной в прямоугольном треугольнике.
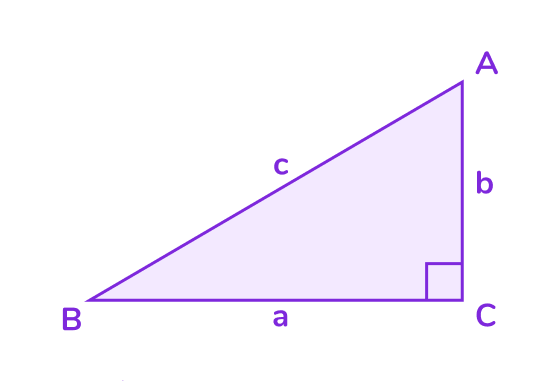
📌 Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90°:
- Если один острый угол равен α, то второй острый угол равен 90° — α.
2. Катет, лежащий напротив угла 30°, равен половине гипотенузы:
- Это свойство особенно полезно при решении задач, где один из острых углов треугольника равен 30°.
3. В равнобедренном прямоугольном треугольнике острые углы равны 45°:
- Если прямоугольный треугольник является равнобедренным (катеты равны), то каждый из острых углов будет равен 45°.
4. Медиана, проведённая к гипотенузе, равна половине гипотенузы:
- Медиана, проведённая из вершины прямого угла, делит гипотенузу пополам и равна её половине.
5. Высота, проведённая из вершины прямого угла, делит треугольник на два подобных треугольника:
- Высота, проведённая к гипотенузе, разбивает исходный треугольник на два треугольника, каждый из которых подобен исходному.
6. Отношение площадей отсечённых треугольников:
- Площади треугольников, образованных высотой, проведённой к гипотенузе, относятся как квадраты прилежащих катетов.
📌 Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула:
𝑐² = 𝑎² + 𝑏²
Где:
- 𝑐 — гипотенуза;
- 𝑎 и 𝑏 — катеты.
Из этой формулы можно выразить длину одного из катетов, если известны гипотенуза и другой катет:
𝑎 = √(𝑐² − 𝑏²);
𝑏 = √(𝑐² − 𝑎²).
📌 Обратная теорема Пифагора
Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то этот треугольник является прямоугольным.
Формула:
𝑐² = 𝑎² + 𝑏² ⇒ треугольник прямоугольный.
Где:
- 𝑐 — наибольшая сторона треугольника (предполагаемая гипотенуза);
- 𝑎 и 𝑏 — две другие стороны.
✏️ Примеры
Прямая теорема:
Дан прямоугольный треугольник с катетами 𝑎 = 3 и 𝑏 = 4. Найдём гипотенузу 𝑐:
𝑐² = 𝑎² + 𝑏² = 3² + 4² = 9 + 16 = 25.
𝑐 = √25 = 5.
Ответ: гипотенуза равна 5.
Обратная теорема:
Дан треугольник со сторонами 𝑎 = 6, 𝑏 = 8, 𝑐 = 10. Проверим, является ли он прямоугольным:
𝑐² = 10² = 100;
𝑎² + 𝑏² = 6² + 8² = 36 + 64 = 100.
Поскольку 𝑐² = 𝑎² + 𝑏², треугольник является прямоугольным.
Ответ: треугольник прямоугольный.
📎 Медианы треугольника
Медиана — это отрезок, проведённый из вершины угла треугольника к противолежащей стороне и делящий эту сторону пополам.
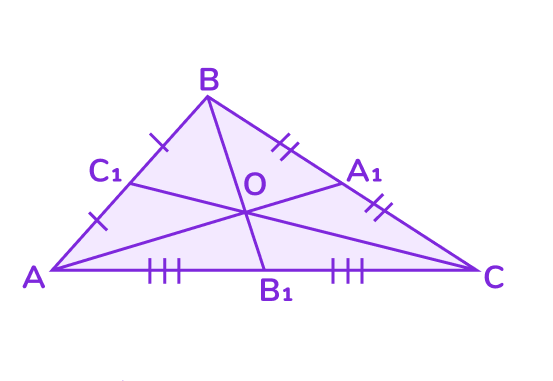
📌 Основные свойства медиан
1. Три медианы треугольника пересекаются в одной точке.
- Эта точка называется центром тяжести треугольника (или центроидом).
- Она делит каждую медиану в отношении 2 : 1, считая от вершины: например, если медиана обозначена как AM , то AO : OM = 2 : 1 , где O — точка пересечения медиан.
2. В равнобедренном треугольнике медианы, проведённые к равным сторонам, равны.
- Третья медиана (проведённая к основанию) является одновременно биссектрисой и высотой.
3. В равностороннем треугольнике все три медианы равны друг другу.
4. В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы.
5. Медиана разбивает треугольник на два равновеликих треугольника.
- Это означает, что площади этих треугольников равны.
- Три медианы разбивают треугольник на шесть равновеликих треугольников.
📎 Биссектрисы треугольника
Биссектриса треугольника — это отрезок, который делит угол треугольника пополам и соединяет вершину этого угла с противоположной стороной.
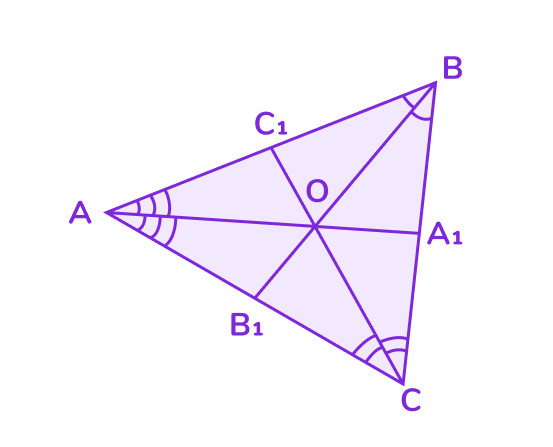
📌 Основные свойства биссектрис
1. Точка пересечения биссектрис:
- Все три биссектрисы треугольника пересекаются в одной точке. Эта точка называется инцентром треугольника.
- Инцентр является центром окружности, вписанной в треугольник.
2. Расстояние до сторон треугольника:
- Любая точка на биссектрисе угла равноудалена от сторон этого угла. Это означает, что расстояние от инцентра до всех сторон треугольника одинаково и равно радиусу вписанной окружности.
3. Отношение деления стороны:
- Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению прилежащих сторон: BD / DC = AB / AC, где AD — биссектриса угла A, а B и C — вершины треугольника.
4. Свойство равнобедренного треугольника:
- В равнобедренном треугольнике биссектриса, проведённая к основанию, является одновременно медианой и высотой.
5. Свойство равностороннего треугольника:
- B равностороннем треугольнике все три биссектрисы равны друг другу.
6. Перпендикулярность внешней и внутренней биссектрис:
- Внутренняя и внешняя биссектрисы одного и того же угла треугольника перпендикулярны друг другу.
📎 Высоты треугольника
Высота треугольника — это перпендикуляр, проведённый из вершины угла к противолежащей стороне (или её продолжению). Высоту обычно обозначают буквой h (или H).
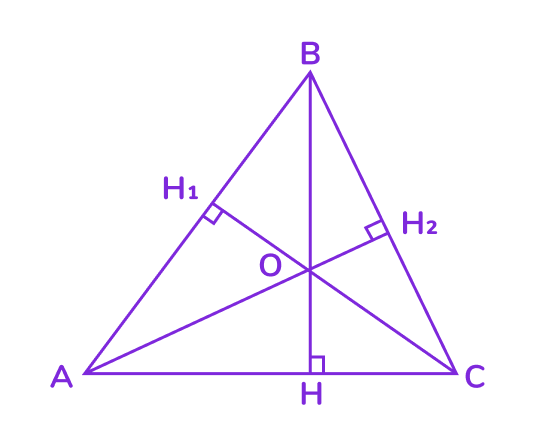
📌 Основные свойства высот треугольника
1. Точка пересечения высот:
- Все три высоты треугольника (или их продолжения) пересекаются в одной точке. Эта точка называется ортоцентром треугольника.
- Расположение ортоцентра зависит от типа треугольника:
— в остроугольном треугольнике ортоцентр находится внутри треугольника;
— в прямоугольном треугольнике ортоцентр совпадает с вершиной прямого угла;
— а в тупоугольном треугольнике ортоцентр лежит вне треугольника.
2. Построение высот:
- Если треугольник остроугольный, то все высоты лежат внутри треугольника.
- Если треугольник тупоугольный, то две высоты выходят за пределы треугольника и падают на продолжение сторон.
3. Особенности прямоугольного треугольника:
- В прямоугольном треугольнике две высоты совпадают с катетами.
- Третья высота проводится из вершины прямого угла к гипотенузе.
4. Связь высот с площадью треугольника:
- Высоту треугольника можно найти через площадь:
h = 2S / a
где:
S — площадь треугольника;
a — сторона, к которой проведена высота.
5. Высота, проведённая из вершины прямого угла:
- Высота, проведённая из вершины прямого угла, делит гипотенузу на два отрезка m и n. При этом выполняется соотношение:
h² = m · n,
где h — высота, проведённая к гипотенузе.
6. Связь между высотой и катетами:
- Высота, проведённая из вершины прямого угла, связана с катетами следующим образом:
1 / h² = 1 / a² + 1 / b²,
где a и b — катеты, а h — высота.
✏️ Пример задачи
Найти высоту треугольника, проведённую к стороне a = 6, если площадь треугольника равна S = 12.
Решение:
Используем формулу:
h = 2S / a.
Подставляем значения:
h = 2 · 12 / 6 = 4.
Ответ: высота равна h = 4.
📎 Средняя линия треугольника
Средняя линия треугольника — это отрезок, который соединяет середины двух сторон треугольника и параллелен третьей стороне.
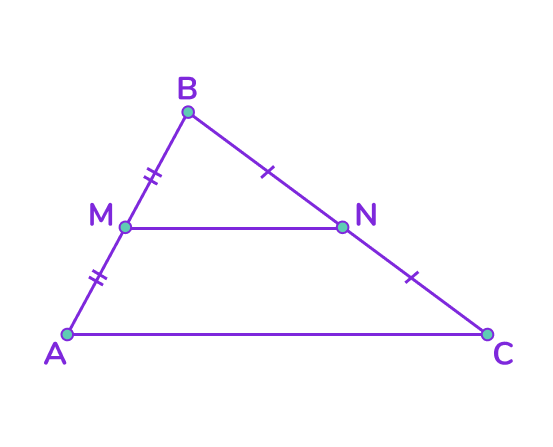
📌 Основные свойства средней линии треугольника
1. Параллельность и длина:
- Средняя линия треугольника всегда параллельна одной из его сторон (стороне, которую она не пересекает).
- Длина средней линии равна половине длины стороны, которой она параллельна:
MN = ½ BC,
где MN — средняя линия, а BC — сторона треугольника.
2. Отсечение подобного треугольника:
- Средняя линия отсекает от треугольника меньший треугольник, который подобен исходному.
- Коэффициент подобия равен ½ , а площадь отсечённого треугольника в 4 раза меньше площади исходного:
S₁ = ¼ S₂,
где S1 — площадь отсечённого треугольника, S2 — площадь исходного.
3. Три средние линии:
- В любом треугольнике можно провести три средние линии.
- Эти линии разделяют треугольник на четыре равновеликих треугольника (треугольники с одинаковой площадью).
✏️ Пример 1
В треугольнике ABC проведена средняя линия MN, соединяющая середины сторон AB и AC . Если длина стороны BC = 8, то длина средней линии MN равна:
MN = ½ BC = ½ ⋅ 8 = 4.
✏️ Пример 2
В треугольнике ABC проведены три средние линии. Площадь исходного треугольника ABC равна 24 . Найдите площадь одного из четырёх треугольников, образованных средними линиями.
Решение:
Площадь каждого из четырёх треугольников равна:
S₁ = ¼ S₂ = ¼ ⋅ 24 = 6.
📎 Периметр и площадь треугольника
👉 Периметр треугольника — это сумма длин всех его сторон.
Формула:
P = a + b + c
где a, b, c — длины сторон треугольника.
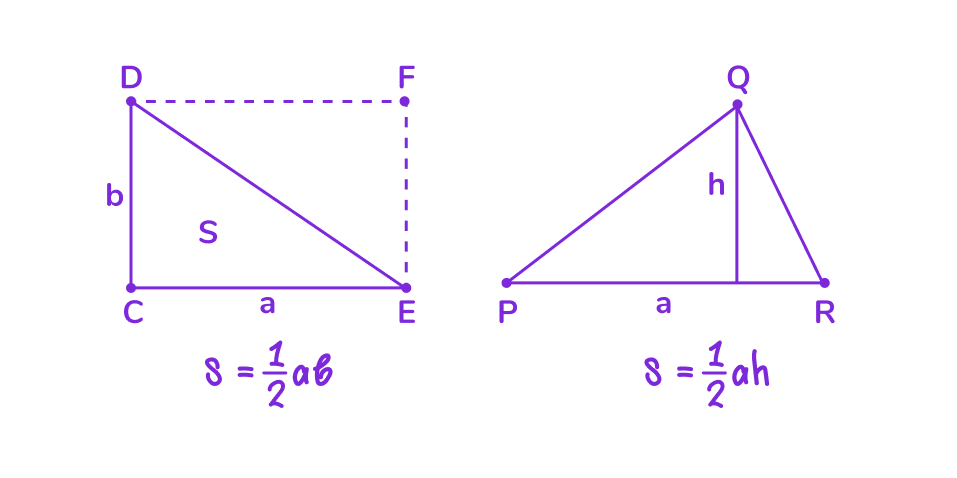
👉 Площадь треугольника можно вычислить разными способами в зависимости от известных данных. Вот основные формулы:
- Через сторону и высоту:
S = ½ · a · hₐ, где: a — сторона треугольника, hₐ — высота, проведённая к этой стороне.
- Через две стороны и угол между ними:
S = ½ · a · b · sin(γ), где: a, b — две стороны треугольника, γ — угол между этими сторонами.
- Формула Герона:
S = √[p · (p — a) · (p — b) · (p — c)], где: p = ½ ⋅ (a + b + c) — полупериметр треугольника, a, b, c — стороны треугольника.
- Для прямоугольного треугольника:
S = ½ · a · b, где: a, b — катеты прямоугольного треугольника.
- Для равностороннего треугольника:
S = (a² · √3) / 4, где: a — сторона равностороннего треугольника.
- Через радиус вписанной окружности:
S = r · p, где: r — радиус вписанной окружности, p = ½ ⋅ (a + b + c) — полупериметр треугольника.
- Через радиус описанной окружности:
S = (a · b · c) / (4R), где: a, b, c — стороны треугольника, R — радиус описанной окружности.
- Через высоту, проведённую из вершины прямого угла (для прямоугольного треугольника):
S = (a · b) / c, где: a, b — катеты, c — гипотенуза.
- Через среднюю линию:
Если треугольник разбит средней линией на два подобных треугольника, то площадь одного из них равна:
S₁ = ¼ · S₂, где: S₂ — площадь исходного треугольника.
📎 Равенство треугольников
Два треугольника называются равными, если их можно совместить наложением так, что все их соответствующие стороны и углы совпадут. Это означает, что:
- соответствующие стороны треугольников равны;
- соответствующие углы треугольников равны.
👉 Существует два способа доказательства равенства треугольников:
Метод наложения:
- Для этого нужно приложить один треугольник к другому таким образом, чтобы их стороны и углы совместились.
- Если все элементы совпадают (три стороны и три угла), то треугольники равны.
Однако метод наложения не всегда удобен, так как требует физического или визуального сравнения всех шести элементов треугольников. Поэтому математики разработали более простые способы — признаки равенства треугольников.
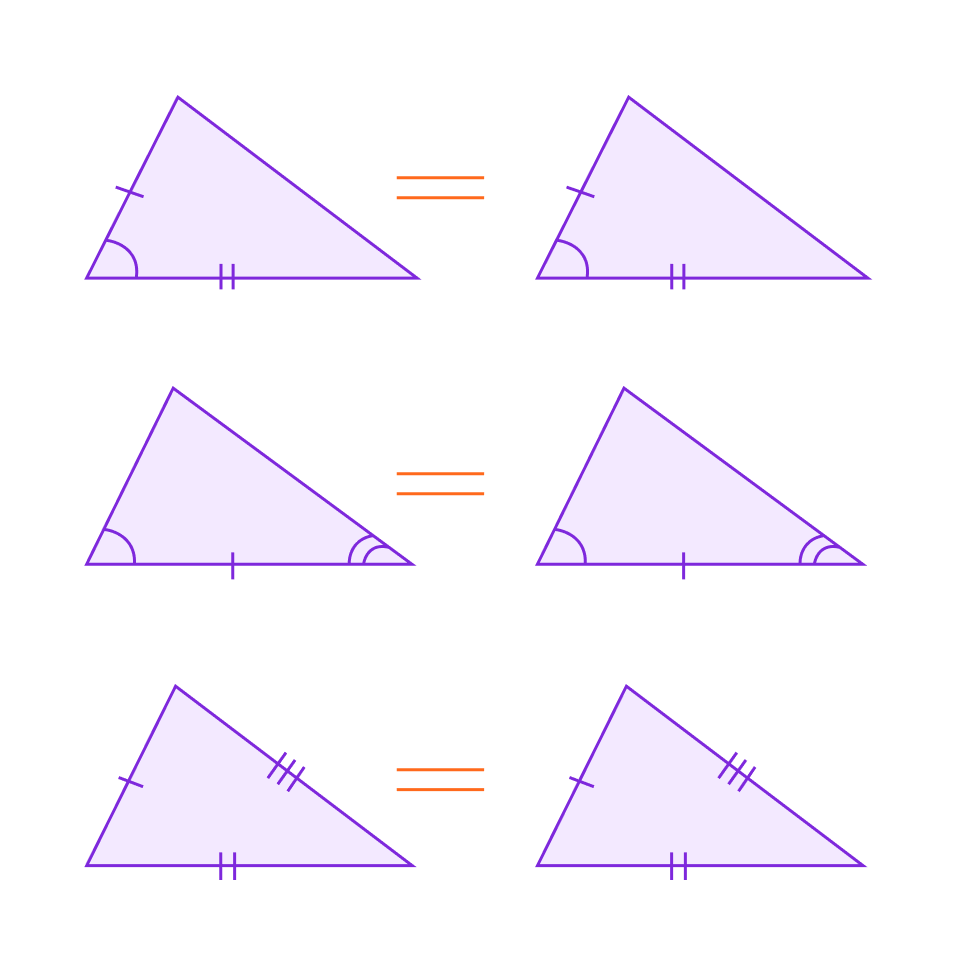
📌 Всего существует три основных признака равенства треугольников:
1. Первый признак равенства треугольников (по двум сторонам и углу между ними):
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
△ABC = △A₁B₁C₁, если AB = A₁B₁, AC = A₁C₁, ∠A = ∠A₁.
2. Второй признак равенства треугольников (по стороне и двум прилежащим углам):
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
△ABC = △A₁B₁C₁, если AB = A₁B₁, ∠A = ∠A₁, ∠B = ∠B₁.
3. Третий признак равенства треугольников (по трём сторонам):
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
△ABC = △A₁B₁C₁, если AB = A₁B₁, BC = B₁C₁, AC = A₁C₁.
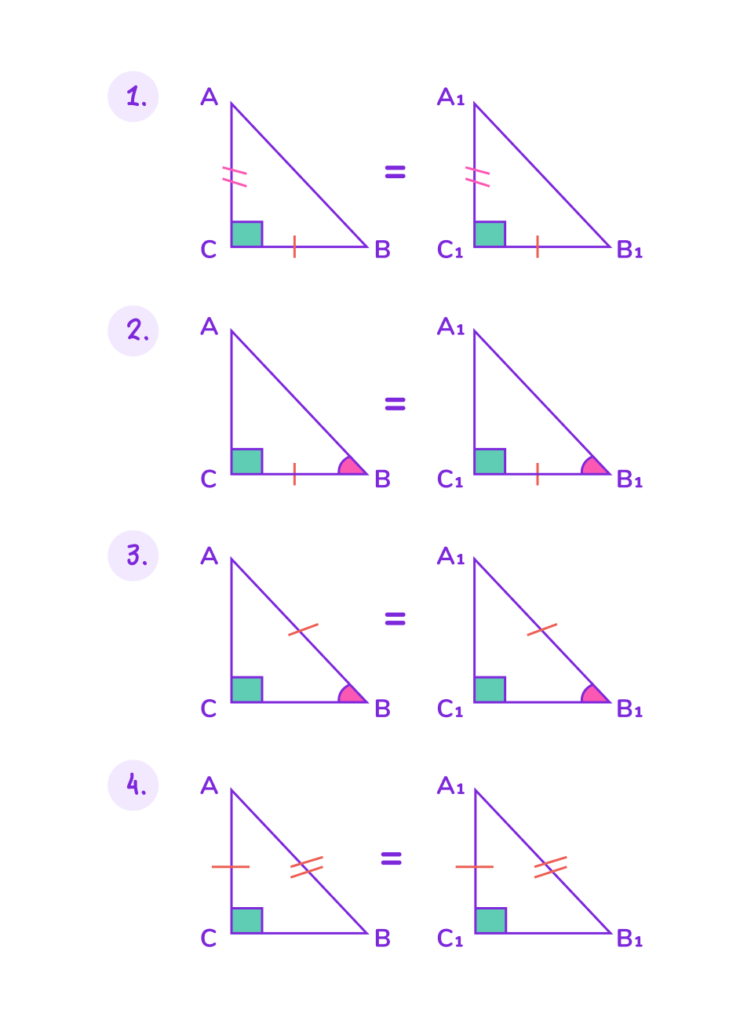
📌 Дополнительные признаки равенства прямоугольных треугольников
Для прямоугольных треугольников существуют ещё четыре дополнительных признака равенства, которые учитывают особенности прямоугольных треугольников (наличие прямого угла, катетов и гипотенузы).
1. По двум катетам:
Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
△ABC = △A₁B₁C₁, если AB = A₁B₁, AC = A₁C₁.
2. По катету и прилежащему острому углу:
Если катет и прилежащий острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
△ABC = △A₁B₁C₁, если AB = A₁B₁, ∠A = ∠A₁.
3. По гипотенузе и острому углу:
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
△ABC = △A₁B₁C₁, если BC = B₁C₁, ∠A = ∠A₁.
4. По гипотенузе и катету:
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
△ABC = △A₁B₁C₁, если BC = B₁C₁, AB = A₁B₁.
📎 Подобие треугольников
Подобие треугольников — это важное понятие в геометрии, которое описывает связь между треугольниками, имеющими одинаковую форму, но разные размеры.
Два треугольника называются подобными, если:
1. Их соответствующие углы равны: ∠A = ∠A₁, ∠B = ∠B₁, ∠C = ∠C₁.
2. Их соответствующие стороны пропорциональны: AB / A₁B₁ = BC / B₁C₁ = AC / A₁C₁ = k, где k — это коэффициент подобия.
Коэффициент подобия показывает, во сколько раз стороны одного треугольника больше (или меньше) сторон другого.
📌 Свойства подобных треугольников
1. Отношение периметров:
- Если два треугольника подобны с коэффициентом k, то их периметры относятся как k: P(△ABC) / P(△A₁B₁C₁) = k.
2. Отношение площадей:
- Площади подобных треугольников относятся как квадрат коэффициента подобия: S(△ABC) / S(△A₁B₁C₁) = k².
3. Соответственные высоты, медианы и биссектрисы:
- Соответственные элементы подобных треугольников также пропорциональны с коэффициентом k.
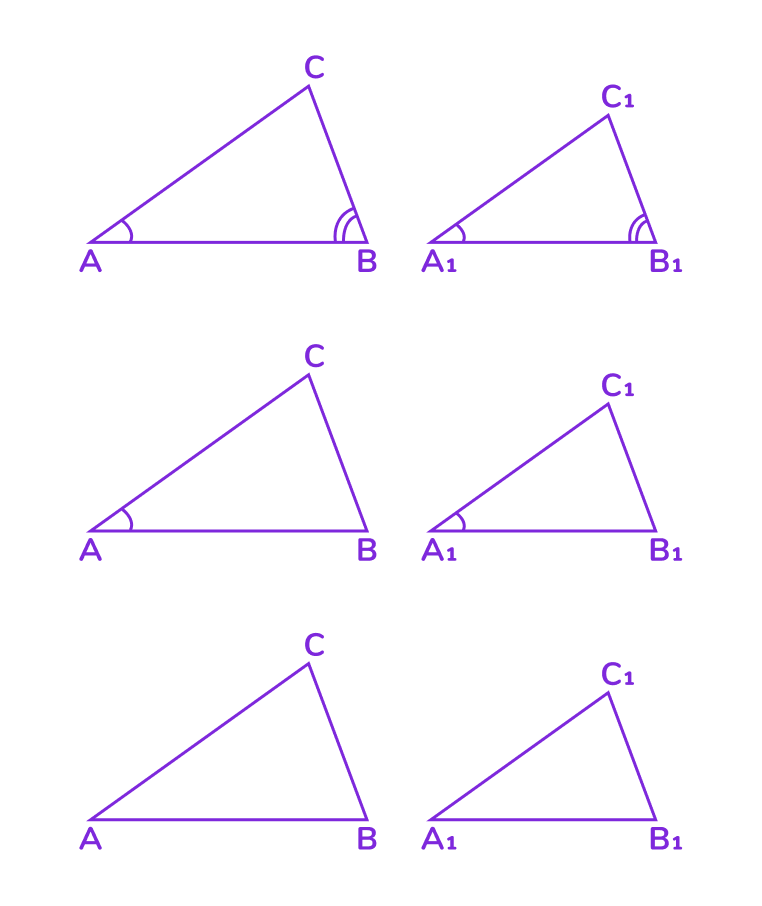
📌 Признаки подобия треугольников
Чтобы доказать, что треугольники подобны, не обязательно проверять все углы и стороны. Достаточно использовать один из трёх основных признаков подобия:
1. Первый признак подобия (по двум углам):
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны:
Если ∠A = ∠A₁ и ∠B = ∠B₁, то △ABC ∼ △A₁B₁C₁.
2. Второй признак подобия (по двум сторонам и углу между ними):
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы между этими сторонами равны, то такие треугольники подобны:
Если AB / A₁B₁ = AC / A₁C₁ и ∠A = ∠A₁, то △ABC ∼ △A₁B₁C₁.
3. Третий признак подобия (по трём сторонам):
- Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны:
Если AB / A₁B₁ = BC / B₁C₁ = AC / A₁C₁, то △ABC ∼ △A₁B₁C₁.
📎 Вписанная и описанная окружность
Вписанная окружность — это окружность, которая касается всех сторон треугольника.
- Центр вписанной окружности называется инцентр.
- Инцентр является точкой пересечения биссектрис треугольника.
Описанная окружность — это окружность, которая проходит через все вершины треугольника.
- Центр описанной окружности является точкой пересечения серединных перпендикуляров к сторонам треугольника.
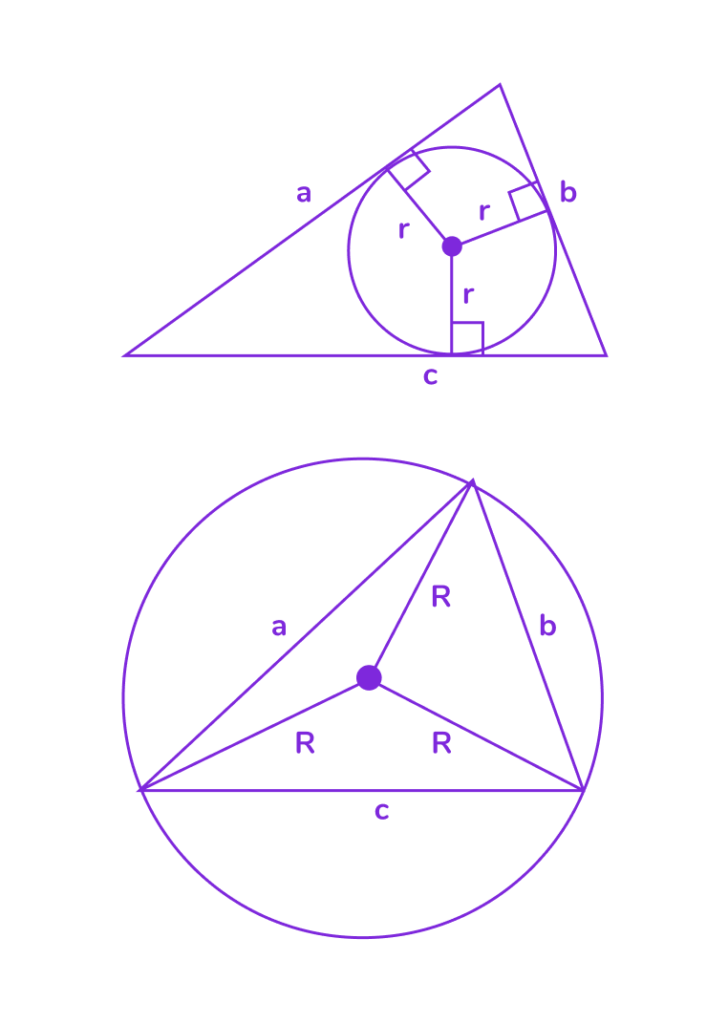
📌 Свойства вписанной окружности
1. В любой треугольник можно вписать окружность, причём только одну.
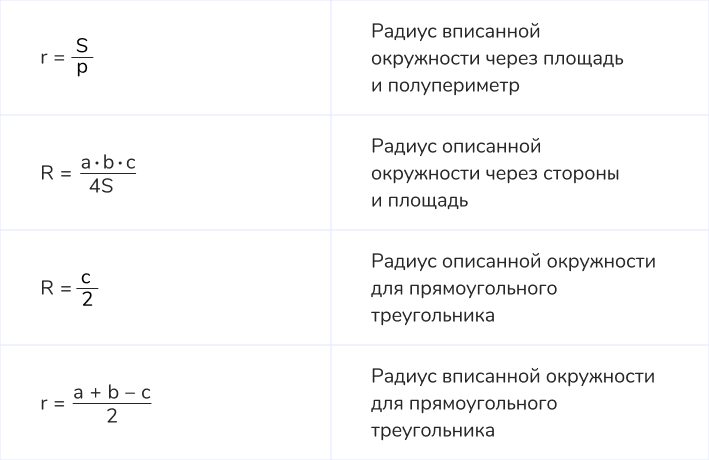
2. Радиус вписанной окружности (r) вычисляется по формуле: r = S / p, где: S — площадь треугольника, p = (a + b + c) / 2 — полупериметр треугольника.
3. Площадь треугольника через радиус вписанной окружности: S = r ⋅ p.
4. Если окружность вписана, то расстояние от центра окружности до любой стороны треугольника равно радиусу r.
5. Для равностороннего треугольника радиус вписанной окружности равен: r = a / (2√3), где a — сторона треугольника.
6. Для прямоугольного треугольника радиус вписанной окружности равен: r = (a + b − c) / 2, где c — гипотенуза, a и b — катеты.
📌 Свойства описанной окружности
1. Около любого треугольника можно описать окружность, причём только одну.
2. Радиус описанной окружности (R) вычисляется по формуле: R = (a ⋅ b ⋅ c) / (4S), где: a, b, c — стороны треугольника, S — площадь треугольника.
3. Для прямоугольного треугольника центр описанной окружности находится на середине гипотенузы, а радиус равен половине гипотенузы: R = c / 2, где c — гипотенуза.
4. Расстояние от центра описанной окружности до вершин треугольника равно радиусу R.
5. Для равностороннего треугольника: радиус описанной окружности равен: R = a/√3, где a — сторона треугольника.
6. Для прямоугольного треугольника: центр описанной окружности всегда лежит на гипотенузе.
7. Связь между радиусами вписанной (r) и описанной (R) окружностей: для любого треугольника: R ≥ 2r.
8. Для равнобедренного треугольника: если треугольник равнобедренный, то центр описанной окружности лежит на высоте, проведённой к основанию.
9. Для тупоугольного треугольника: центр описанной окружности лежит вне треугольника.
10. Для остроугольного треугольника: центр описанной окружности лежит внутри треугольника.
📌 Дополнительные свойства
1. Формула Эйлера:
Расстояние между центром вписанной (I) и описанной (O) окружностей выражается формулой: d² = R²−2Rr, где: d — расстояние между центрами, R — радиус описанной окружности, r — радиус вписанной окружности.
2. Связь с углами треугольника: для описанной окружности: a / sin(A) = b / sin(B) = c / sin(C) = 2R, где A , B , C — углы треугольника, a, b, c — стороны.
3. Положение центров окружностей:
- Центр вписанной окружности всегда лежит внутри треугольника.
- Центр описанной окружности может лежать внутри (для остроугольного треугольника), на стороне (для прямоугольного треугольника) или вне треугольника (для тупоугольного треугольника).
📎 Свойства углов и сторон треугольника
1. Сумма внутренних углов любого треугольника равна 180°:
∠A + ∠B + ∠C = 180°
2. В прямоугольном треугольнике сумма острых углов равна 90°:
∠A + ∠B = 90°
3. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним:
∠внешний = ∠A + ∠B
4. В треугольнике напротив большего угла лежит большая сторона, а напротив меньшего угла — меньшая сторона:
Если ∠A > ∠B, то BC > AC.
5. Сумма длин любых двух сторон треугольника всегда больше длины третьей стороны:
a + b > c
b + c > a
a + c > b
6. Теорема синусов
Для любого треугольника отношение стороны к синусу противолежащего угла одинаково и равно диаметру описанной окружности:
a / sin(A) = b / sin(B) = c / sin(C) = 2R
7. Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
c² = a² + b² — 2ab · cos(γ)
8. Теорема Пифагора (для прямоугольного треугольника)
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
9. Катет, лежащий напротив угла 30°
В прямоугольном треугольнике катет, лежащий напротив угла 30°, равен половине гипотенузы:
a = c / 2
10. В равнобедренном треугольнике углы при основании равны, а медиана, биссектриса и высота, проведённые к основанию, совпадают.
11. В равностороннем треугольнике все стороны и углы равны, каждый угол равен 60°:
∠A = ∠B = ∠C = 60°
12. Высота, проведённая из вершины прямого угла, делит гипотенузу на отрезки m и n, причём:
h² = m · n
13. Медиана делит сторону треугольника пополам. Три медианы пересекаются в одной точке (центре тяжести), которая делит каждую медиану в отношении 2:1.
14. Биссектриса делит угол пополам. Она также делит противоположную сторону в отношении, равном отношению прилежащих сторон.
📋 Памятка с формулами
1. Площадь треугольника

2. Периметр треугольника

3. Теоремы для треугольников

4. Высоты треугольника

5. Медианы треугольника

6. Биссектрисы треугольника

7. Радиусы вписанной и описанной окружностей
8. Средняя линия треугольника

9. Углы треугольника

10. Прямоугольный треугольник
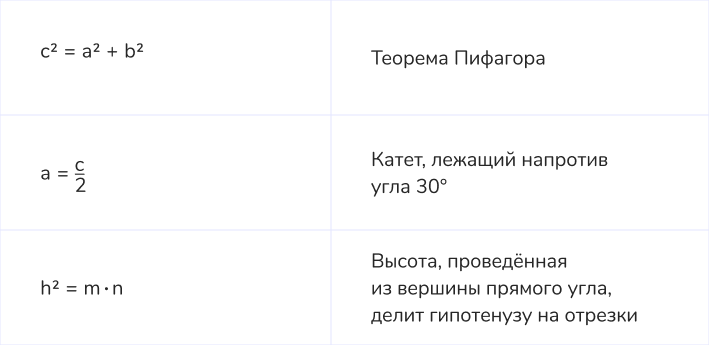
11. Подобие треугольников
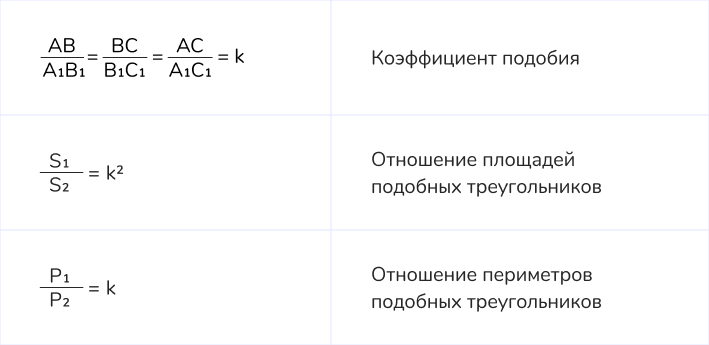
12. Окружности и треугольники
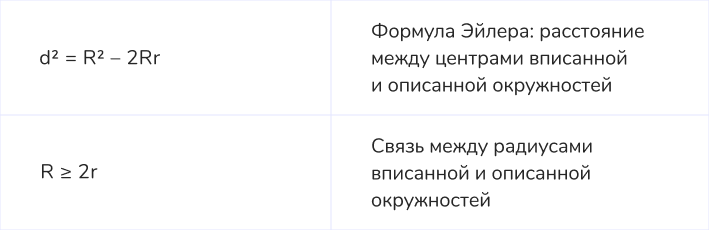
13. Свойства равнобедренного треугольника
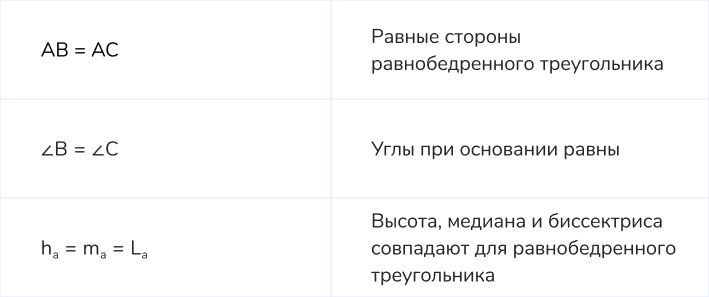
14. Свойства равностороннего треугольника
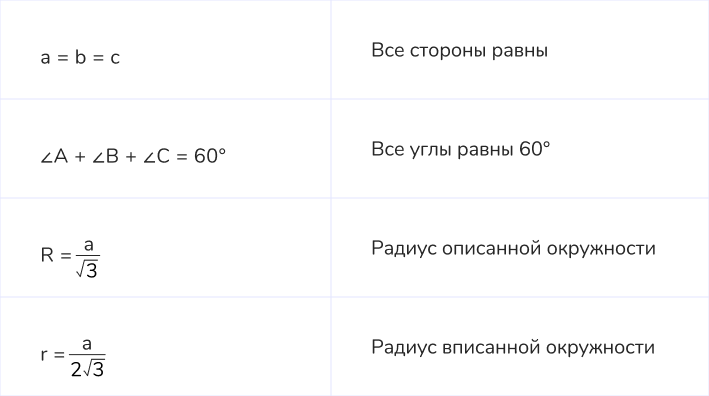
✏️
Треугольник — это базовая геометрическая фигура, состоящая из трёх сторон и трёх вершин, с фиксированными свойствами и разнообразными видами (остроугольный, прямоугольный, тупоугольный, равнобедренный, равносторонний). Важными элементами треугольника являются высоты, медианы, биссектрисы, средние линии, а также вписанная и описанная окружности. Для решения задач используются ключевые теоремы: Пифагора, синусов, косинусов, а также признаки подобия и равенства треугольников.
Треугольники играют центральную роль в геометрии, так как их свойства применяются для анализа более сложных фигур и решения практических задач.
Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы!
 3
3
 1
1
 0
0








Комментарии 0