Куб: основные элементы и свойства

Куб — одна из самых удивительных и гармоничных геометрических фигур, которая привлекает внимание своей симметрией и универсальностью. Эта тема особенно актуальна для учащихся 10-го класса, которые начинают глубже изучать стереометрию и знакомятся с трёхмерными фигурами. Понимание свойств куба позволяет не только решать задачи на уроках геометрии, но и развивать пространственное мышление, необходимое для освоения более сложных разделов математики.

В статье мы подробно рассмотрим, что такое куб, из чего он состоит, и разберём его основные элементы: грани, рёбра, вершины, диагонали и оси. Особое внимание будет уделено свойствам куба, таким как площадь поверхности, периметр, объём, а также взаимосвязь куба со сферой и координатами вершин. 

Что такое куб и из чего он состоит 

🖇️ Куб — это уникальная геометрическая фигура, которая представляет собой правильный многогранник. Его особенность заключается в том, что все его элементы равны и симметричны. Куб состоит из определённого количества элементов, каждый из которых играет важную роль в его структуре.

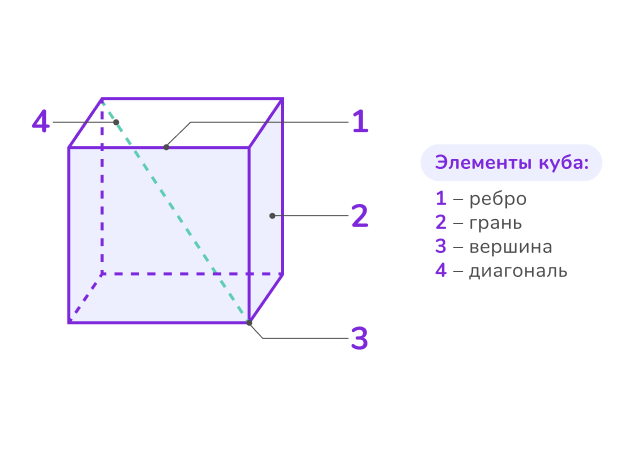
Основные элементы куба ⤵

1. Грани (6 штук)
Грани куба — это плоские поверхности, ограничивающие его. Все грани куба являются равными квадратами. Именно благодаря этому свойству куб выглядит одинаково со всех сторон.

2. Рёбра (12 штук)
Рёбра — это отрезки, которые соединяют соседние вершины куба. Все рёбра куба имеют одинаковую длину, что делает его идеально пропорциональным.

3. Вершины (8 штук)
Вершины — это точки пересечения трёх рёбер. В каждой вершине куба сходятся три грани, образуя угол в 90 градусов.

4. Диагонали

1. Диагонали граней: каждая грань куба имеет две диагонали, которые соединяют противоположные углы квадрата. У куба всего 12 диагоналей граней (по 2 на каждую из 6 граней).
2. Пространственные диагонали: это диагонали, которые соединяют противоположные вершины куба через его внутреннее пространство. У куба их всего 4.

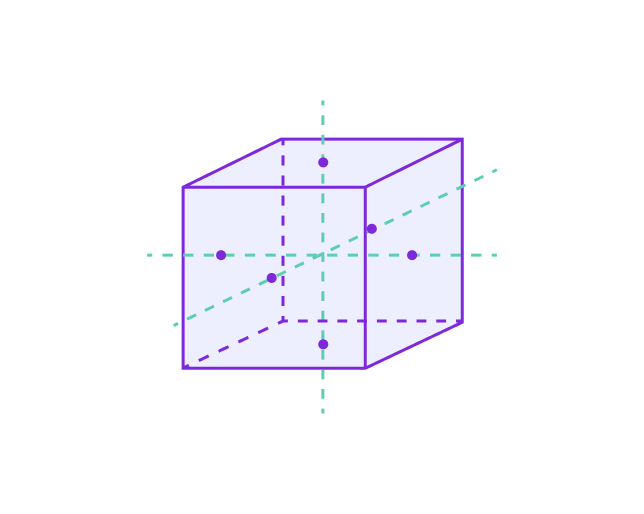
Определение осей куба:

1. Ось куба — это прямая, которая проходит через центр куба и центры двух его параллельных граней.
2. У куба есть три оси, так как у него шесть граней, которые попарно параллельны.

Взаимное расположение осей:

1. Все три оси взаимно перпендикулярны друг другу. Это связано с тем, что грани куба также расположены под прямым углом друг к другу.
2. Каждая ось соответствует одной из пространственных координат (например, x, y, z), если куб расположен в декартовой системе координат.

Площадь поверхности, периметр и объём куба

Куб — это правильный многогранник, все стороны которого равны. Для решения задач важно знать формулы для вычисления его площади поверхности, периметра и объёма.

📌 Площадь поверхности куба

Площадь поверхности куба — это сумма площадей всех его граней. У куба 6 граней, каждая из которых является квадратом. Чтобы найти площадь поверхности, нужно умножить площадь одной грани на 6. Если длина ребра куба равна a, то площадь поверхности можно вычислить так:

Например: если длина ребра куба равна 10, то площадь поверхности будет равна:

S = 6 ∙ 10² = 6 ∙ 100 = 600.

📌 Периметр куба

Периметр куба — это сумма длин всех его рёбер. У куба 12 рёбер, и все они равны между собой. Чтобы найти периметр, нужно умножить длину одного ребра на 12:

Например: если длина ребра куба равна 10, то периметр будет равен:

P = 12 ∙ 10 = 120.

📌 Объём куба

Oбъём куба — это количество пространства, которое занимает фигура. Чтобы найти объём, нужно перемножить длины трёх рёбер, выходящих из одной вершины. Так как все рёбра куба равны, объём можно вычислить так:

Например: если длина ребра куба равна 10, то объём будет:

V = 10³ = 10 ∙ 10 ∙ 10 = 1000.

Также объём куба можно вычислить, зная длину его диагонали. Если диагональ куба равна d, то объём можно найти по формуле:

Куб и сфера

Kуб и сфера — это две фундаментальные геометрические фигуры, которые часто рассматриваются вместе из-за их уникальных взаимосвязей. Сфера может быть как вписана в куб, так и описана вокруг него. Эти соотношения играют важную роль в решении задач стереометрии.

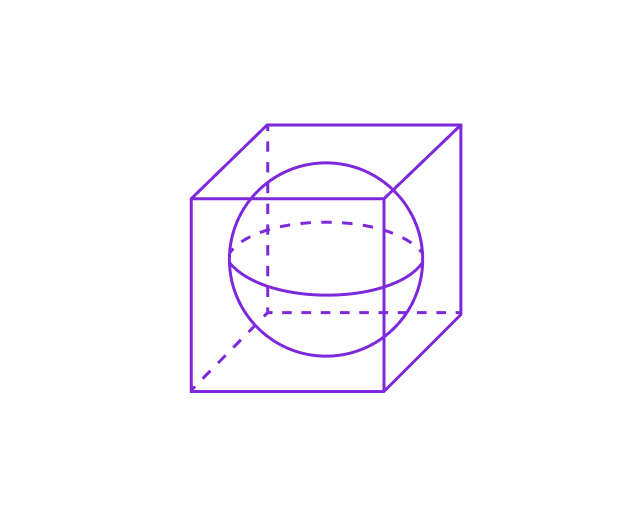
📌 Вписанная сфера

Вписанная сфера — это сфера, которая касается всех граней куба в их центрах.

1. Центр вписанной сферы совпадает с центром куба.
2. Радиус вписанной сферы равен половине длины ребра куба: r = a / 2, где a –– длина ребра куба.
3. Объём вписанной сферы можно вычислить по формуле: V = (4 / 3) ∙ π ∙ r³ = (4 / 3) ∙ π ∙ (a / 2)³ = (π ∙ a³) / 6.

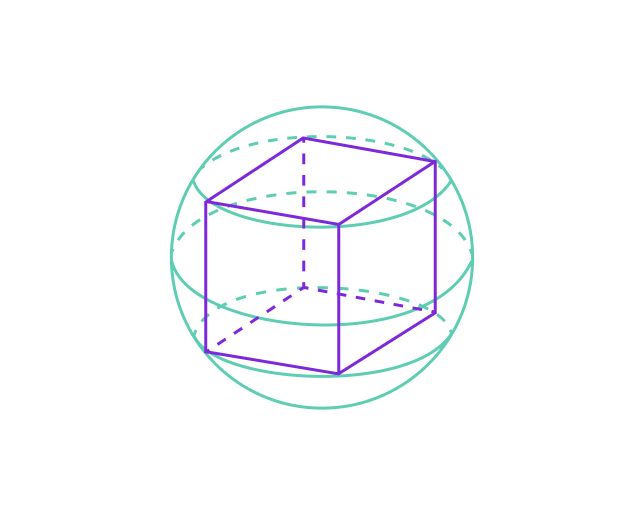
📌 Описанная сфера

Описанная сфера — это сфера, которая проходит через все вершины куба.

1. Центр описанной сферы также совпадает с центром куба.
2. Радиус описанной сферы равен половине длины пространственной диагонали куба: R = d / 2 = (a ∙ √3) / 2, где d = a ∙ √3 –– диагональ куба.
3. Объём описанной сферы вычисляется по формуле: V = (4/3) ∙ π ∙ R³ = (4/3) ∙ π ∙ ((a ∙ √3) / 2)³ = (π ∙ a³ ∙ √3) / 2.

📌 Геометрические свойства:

1. Соотношение радиусов: радиус описанной сферы всегда больше радиуса вписанной сферы. Их соотношение: R / r = √3.

2. Положение центров: центры обеих сфер совпадают с центром куба, что подчеркивает высокую степень симметрии этой фигуры.

Свойства куба

Куб — это уникальная геометрическая фигура, обладающая рядом важных свойств. Эти свойства делают его одной из самых симметричных и удобных фигур для изучения в геометрии.

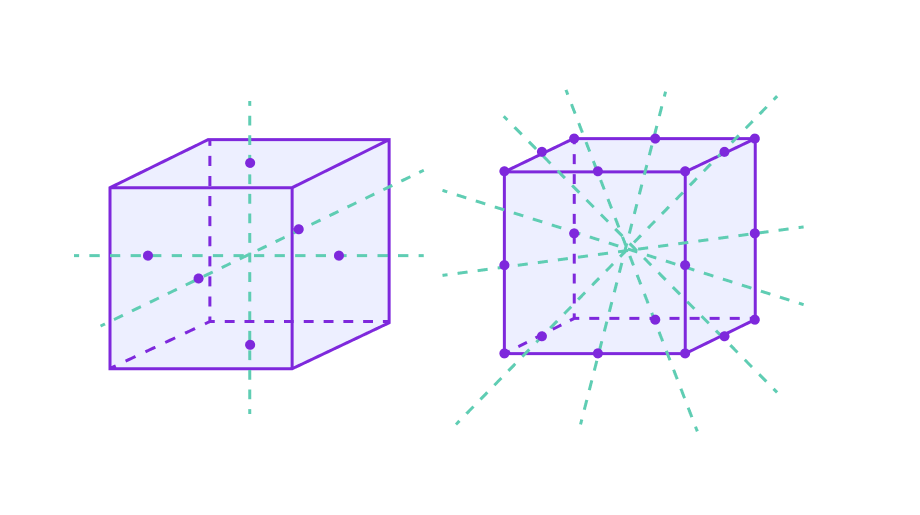
Куб имеет высокую степень симметрии. У него есть 9 осей симметрии:

1. 3 оси проходят через центры противоположных граней.
2. 4 оси проходят через противоположные вершины.
3. 2 оси проходят через середины противоположных рёбер.

Диагонали куба:

1. У куба есть 4 пространственные диагонали, которые соединяют противоположные вершины. Длина каждой диагонали вычисляется по формуле: d = a ∙ √3, где a — длина ребра куба.
2. Диагонали всех граней равны между собой, их длина равна: d = a ∙ √2.

Вписанная и описанная сфера:

1. В куб можно вписать сферу, радиус которой равен половине длины ребра: r = a / 2.
2. Bокруг куба можно описать сферу, радиус которой равен половине длины пространственной диагонали: R = (a ∙ √3) / 2.
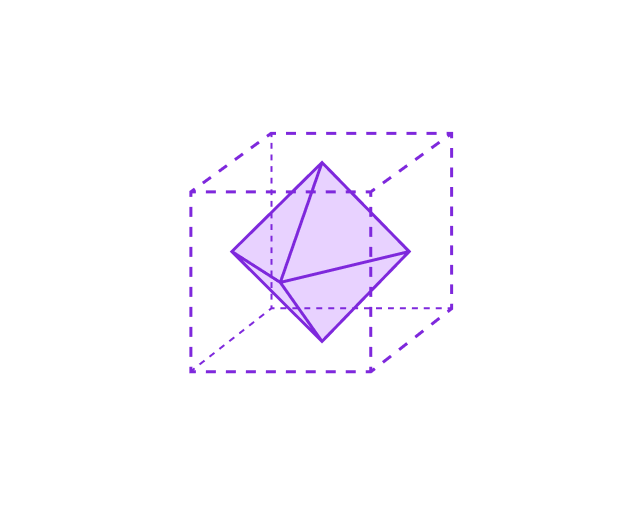
3. В куб можно вписать тетраэдр так, чтобы все 4 вершины тетраэдра совпадали с вершинами куба. Рёбра тетраэдра будут равны диагонали грани куба: d = a ∙ √2.

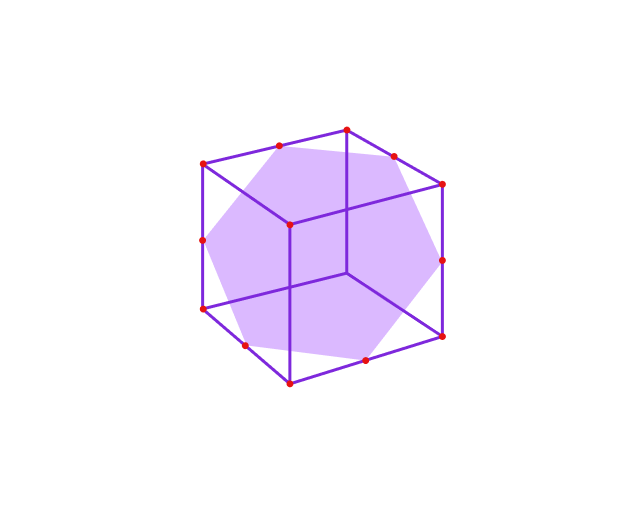
Шестиугольник внутри куба:

1. В куб можно вписать правильный шестиугольник так, что все 6 вершин шестиугольника будут находиться в центрах граней куба.

Перпендикулярность рёбер:

1. Все рёбра куба пересекаются под углом 90°. Это свойство делает куб идеальной моделью для изучения трёхмерной системы координат.

Равенство всех элементов:

1. Все грани куба — равные квадраты.
2. Bсе рёбра куба имеют одинаковую длину.
3. Все углы между гранями прямые (90°).

Координаты вершин куба

Куб — это фигура в трёхмерном пространстве, и каждая его точка имеет координаты в системе координат. Если расположить куб так, чтобы его рёбра были параллельны осям координат, то координаты его вершин можно легко определить.

1. Куб с началом координат в одной из вершин

Если одна из вершин куба находится в начале координат (точка (0, 0, 0)), а длина ребра равна a, то координаты всех вершин будут следующими:

1. A(a, 0, 0);
2. B(a, a, 0);
3. C(0, a, 0);
4. D(0, 0, 0);
5. E(a, 0, a);
6. F(a, a, a);
7. G(0, a, a);
8. H(0, 0, a).

Здесь:

A, B, C, D — это вершины нижней грани куба.

E, F, G, H — это вершины верхней грани куба.

2. Куб с центром в начале координат

Если центр куба совпадает с началом координат, а длина ребра равна 2a, то координаты вершин будут такими:

1. A(a, -a, -a);
2. B(a, a, -a);
3. C(-a, a, -a);
4. D(-a, -a, -a);
5. E(a, -a, a);
6. F(a, a, a);
7. G(-a, a, a);
8. H(-a, -a, a).

Здесь:

A, B, C, D — это вершины нижней грани куба.

E, F, G, H — это вершины верхней грани куба.

3. Единичный куб

Единичный куб — это куб, у которого все рёбра имеют длину, равную единице. Если одна из его вершин находится в начале координат, то координаты вершин будут такими:

1. A(1, 0, 0);
2. B(1, 1, 0);
3. C(0, 1, 0);
4. D(0, 0, 0);
5. E(1, 0, 1);
6. F(1, 1, 1);
7. G(0, 1, 1);
8. H(0, 0, 1).

Свойства:

1. Каждая вершина куба соединена с тремя соседними вершинами рёбрами.
2. Все грани куба — это квадраты, и их стороны равны длине ребра куба.

Пересечение куба плоскостью

Когда плоскость пересекает куб, форма сечения зависит от того, как именно эта плоскость расположена относительно граней и рёбер куба. Рассмотрим основные случаи пересечения:

1. Сечение — квадрат

Если плоскость проходит через центр куба параллельно одной из его граней, то в сечении получится квадрат.

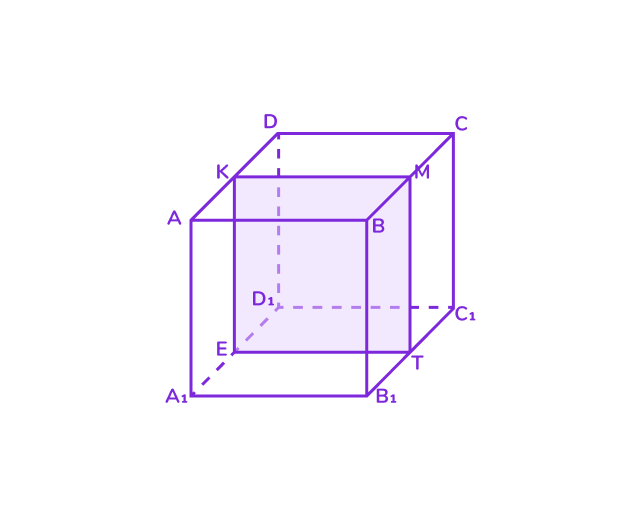
2. Сечение — прямоугольник

Если плоскость проходит через центр куба и два его параллельных ребра, то в сечении получится прямоугольник.

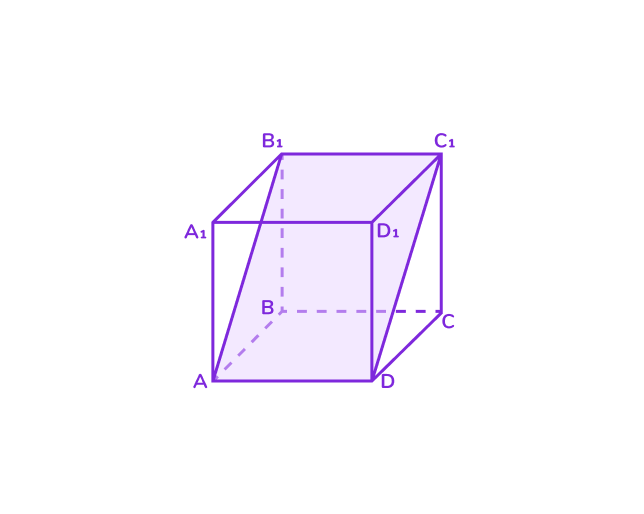
3. Сечение — правильный треугольник

Если плоскость проходит через три вершины куба, то в сечении получится правильный треугольник.

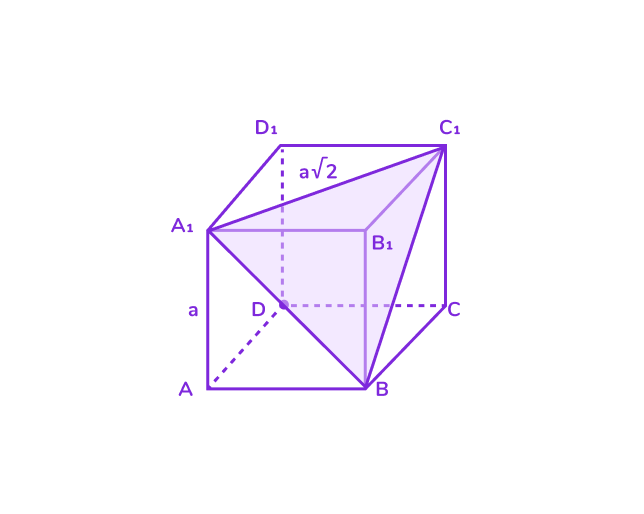
4. Сечение — правильный шестиугольник

Если плоскость проходит через центр куба и середины шести его граней, то в сечении получится правильный шестиугольник.

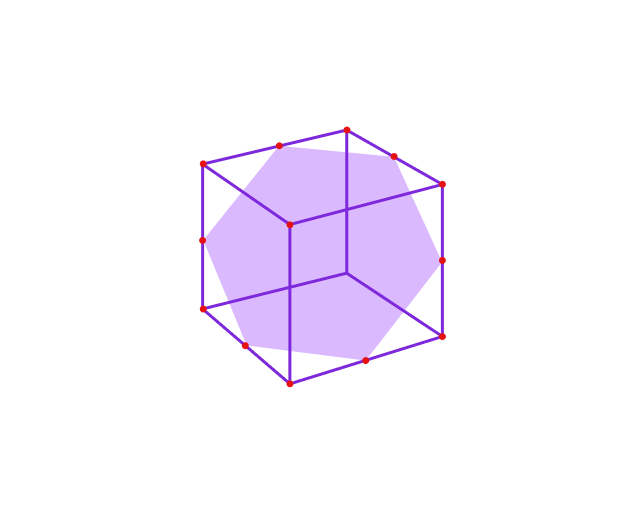
5. Сечение — трапеция

Если плоскость пересекает одну из боковых граней куба и его основание, то в сечении может получиться трапеция.

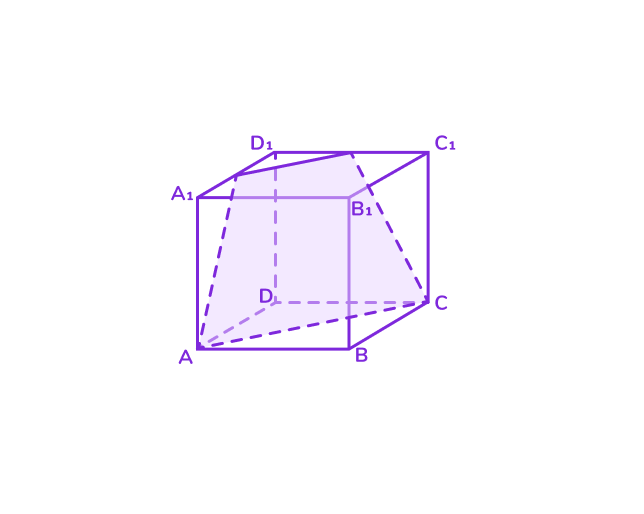
Памятка с формулами

Куб — это не только простая и элегантная геометрическая фигура, но и мощный инструмент для понимания законов симметрии, пространственных отношений и математического моделирования. Его свойства находят применение в архитектуре, физике, компьютерной графике и многих других областях. Изучение куба помогает развивать пространственное мышление и навыки решения задач, что особенно важно для подготовки к экзаменам и дальнейшего обучения.