
Что такое функция
Функция — это одно из самых важных понятий в математике, с которым ученики начинают знакомиться в 7-м классе. Функция помогает описывать и анализировать взаимосвязи между различными величинами. Например, как меняется температура в течение дня, как зависит стоимость покупки от количества товаров или как движется автомобиль по дороге. Все эти процессы можно описать с помощью функций.
В этой статье мы подробно разберём, что такое функция, как она задаётся и как её можно использовать для решения задач.

Понятие функции
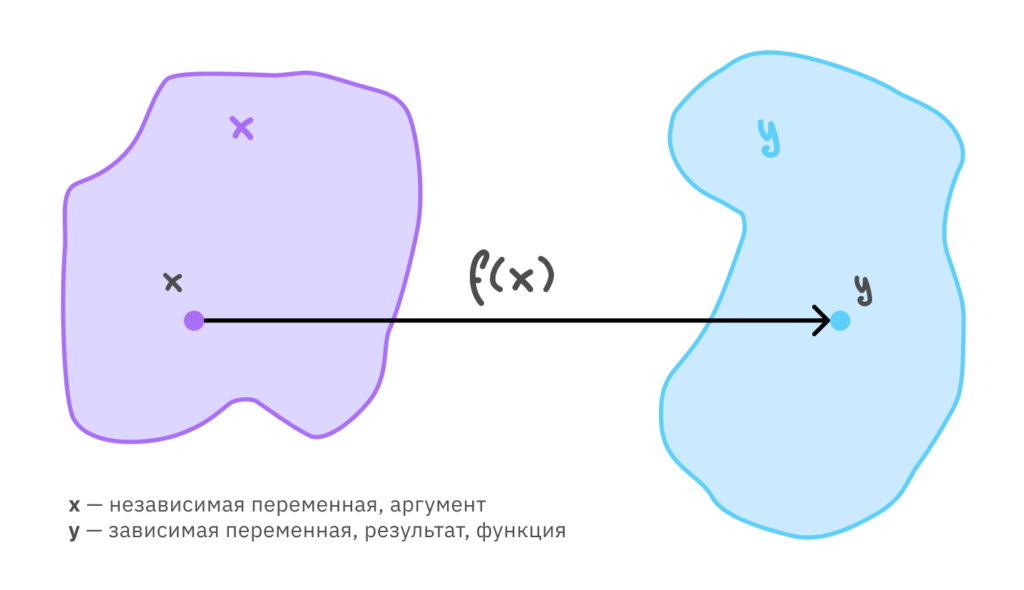
📎 Функция — это правило, которое каждому значению одной величины (называемой аргументом или x) ставит в соответствие единственное значение другой величины (называемой y).
Обозначается функция обычно как y = f(x) , где:
- x — независимая переменная (аргумент);
- y — зависимая переменная (значение функции);
- f — правило, связывающее x и y.
💡
Простыми словами, функция показывает, как изменение одного числа влияет на другое. Например, если вы покупаете конфеты по цене 20 рублей за штуку, то общая стоимость покупки зависит от количества конфет. Это и есть пример функции:
y = 20x,
где x — количество конфет, а y — стоимость покупки.
Ещё один способ понять функцию — представить её как устройство, которое «перерабатывает» входные данные (x) в выходные (y). Например, если вы вводите число в калькулятор, он выполняет операцию и выдаёт результат.
Область определения и область значений ⤵
📎 Oбласть определения — это множество всех допустимых значений x, при которых функция имеет смысл. Например, для функции y = 1 / x область определения: x ≠ 0 , так как деление на ноль невозможно.
📎 Область значений — это множество всех возможных значений y, которые функция может принимать. Например, для функции y = x² область значений: y ≥ 0, так как квадрат любого числа неотрицателен.
Способы задания функций
Функцию можно описать разными способами. Каждый из них имеет свои особенности и подходит для разных задач. Рассмотрим основные способы задания функций ⤵
1. Задание функции формулой
Это самый распространённый и удобный способ. Функция записывается в виде формулы, которая показывает, как найти значение y, зная значение x. Например:
- y = 2x + 5 — линейная функция;
- y = x² − 3x + 4 — квадратичная функция.
Преимущество этого способа в том, что формула позволяет быстро вычислить значение функции для любого значения аргумента. Например, если y = 2x + 5 и x = 3, то:
y = 2 ⋅ 3 + 5 = 6 + 5 = 11.
Также формула помогает анализировать свойства функции, такие как возрастание, убывание или наличие экстремумов.
2. Задание функции таблицей
В этом случае функция задаётся в виде таблицы, где указаны значения x и соответствующие им значения y.
Пример ⤵

Таблица удобна, когда нужно быстро найти конкретные значения функции. Например, из таблицы видно, что при x = −2 значение y = 4. Однако этот способ не всегда нагляден, особенно если нужно понять общее поведение функции.
3. Задание функции графиком
📎 График функции — это множество точек на координатной плоскости, где каждая точка имеет координаты (x;y). График наглядно показывает, как изменяется функция, и помогает анализировать её свойства.
Пример ⤵
Для функции y=x² графиком будет парабола. Если подставить значения x = −2, −1, 0, 1, 2 , то получим точки:
(−2;4), (−1;1), (0;0), (1;1), (2;4).
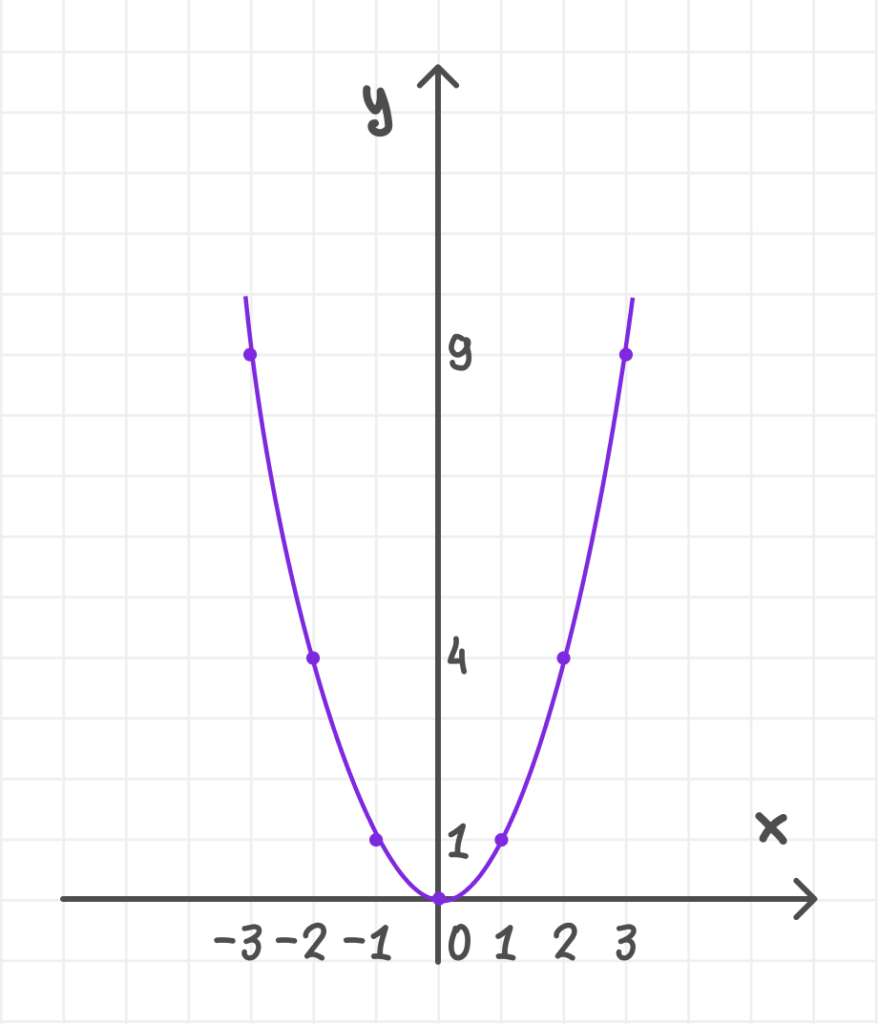
Эти точки можно отметить на плоскости и соединить плавной линией.График позволяет сразу увидеть, где функция возрастает, где убывает, есть ли максимумы или минимумы.
📌 Важные замечания
1. Выбор способа зависит от задачи:
- Если нужно быстро вычислить значения, используйте формулу.
- Если важно наглядно увидеть поведение функции, постройте график.
- А если данные уже собраны, используйте таблицу.
2. Переход между способами:
- Из формулы можно построить график или составить таблицу.
- Из графика можно определить формулу (если график достаточно простой).
Функция — это важный инструмент в математике, который помогает описывать зависимости между величинами. Мы рассмотрели три основных способа задания функции: формулой, таблицей и графиком. Каждый из них имеет свои преимущества. Понимание этих способов поможет вам уверенно решать задачи и анализировать процессы в реальной жизни. Продолжайте практиковаться, и вы станете настоящим мастером работы с функциями.
Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы. Первый урок по форме ниже — бесплатный!
 15
15
 20
20
 14
14








Спасибо ❤️
Как решается квадратическая функция? Как решается задача по таблице? Ничего не объяснили, что понял, то понял. Максимум нам под таблицей написано, мол «x=-2 и значение y=4», и этот способ не всегда нагляден… Что за способ? Как решается? Статься, не сказал бы, что лчшая…