Арифметическая прогрессия

Арифметическая прогрессия — это одна из важнейших тем в курсе алгебры 9-го класса. Она помогает понять, как устроены числовые последовательности, и применяется в различных задачах: от расчёта финансовых платежей до анализа физических процессов. В этой статье мы разберём определение арифметической прогрессии, её свойства, формулы для вычисления n-го члена и суммы первых n членов, а также решим несколько задач. 

Определение числовой последовательности

📎 Числовая последовательность — это набор чисел, расположенных в определённом порядке. Каждое число в последовательности называется членом последовательности. Последовательности могут быть:

1. конечными — если количество членов ограничено;
2. бесконечными — если последовательность продолжается бесконечно.

Примеры:

1. конечная последовательность: 2, 4, 6, 8;
2. бесконечная последовательность: 1, 2, 3, 4, … .

Способы задания последовательностей

Последовательности можно задавать несколькими способами ⤵︎

1. Аналитический способ

Последовательность задаётся формулой n-го члена. Например:

1. Арифметическая прогрессия: aₙ = a₁ + (n — 1) · d.
2. Геометрическая прогрессия: bₙ = b₁ · qⁿ⁻¹.

Пример:

aₙ = 2n + 3 ⇒ 5, 7, 9, 11, ….

2. Рекуррентный способ

Каждый следующий член последовательности выражается через предыдущие. Например:

1. Арифметическая прогрессия: aₙ₊₁ = aₙ + d.
2. Геометрическая прогрессия: bₙ₊₁ = bₙ · q.

Пример:

a₁ = 2, aₙ₊₁ = aₙ + 3 ⇒ 2, 5, 8, 11, ….

3. Словесный способ

Последовательность описывается словами. Например:

1. «Каждое следующее число на 4 больше предыдущего».
2. «Первый член равен 1, а каждый следующий в два раза больше предыдущего».

4. Табличный способ

Последовательность задаётся в виде таблицы, где указаны номера членов и их значения.

5. Графический способ

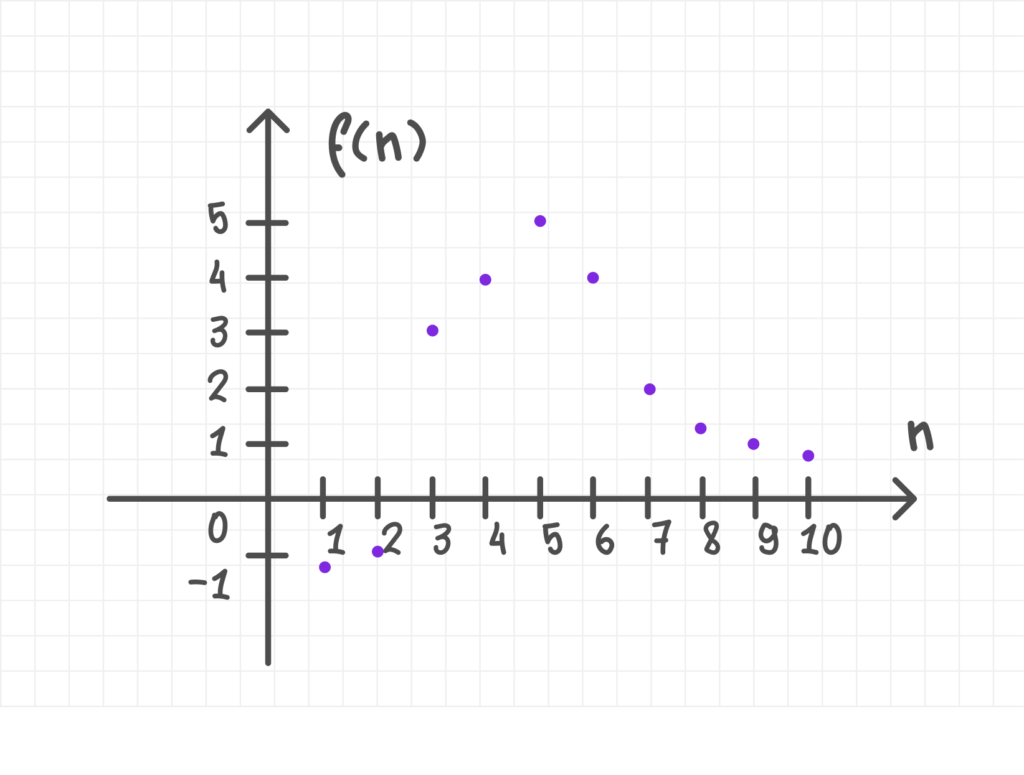
Члены последовательности изображаются точками на координатной плоскости с координатами (n, aₙ). Например:

1. Для арифметической прогрессии точки лежат на прямой.
2. Для геометрической прогрессии точки лежат на кривой.

Определение арифметической прогрессии

📎 Арифметическая прогрессия — это числовая последовательность, в которой каждый следующий член отличается от предыдущего на одно и то же число. Это число называется разностью арифметической прогрессии и обозначается как d .

Формально:

aₙ₊₁ = aₙ + d

где:

1. aₙ — текущий член прогрессии;
2. aₙ₊₁ — следующий член прогрессии;
3. d — разность прогрессии.

Если известны первый член a₁ и n-й член прогрессии aₙ, разность d можно найти по формуле:

d = (aₙ — a₁) / (n — 1)

Арифметическая прогрессия бывает трёх видов:

1. Возрастающая — если разность d > 0. Пример: 2, 5, 8, 11, 14 (здесь d = 3).
2. Убывающая — если разность d < 0. Пример: 10, 7, 4, 1, -2 (здесь d = -3).
3. Стационарная — если разность d = 0. Пример: 5, 5, 5, 5 (здесь d = 0).

Свойство арифметической прогрессии

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних членов. Это свойство можно записать в виде формулы:

aₙ = (aₙ₋₁ + aₙ₊₁) / 2

где:

1. aₙ — текущий член прогрессии;
2. аₙ₋₁ — предыдущий член;
3. aₙ₊₁ — следующий член.

Это свойство позволяет проверить, является ли последовательность арифметической прогрессией, или найти неизвестный член, если известны его соседние члены.

Формула n-го члена арифметической прогрессии

Формула для нахождения n-го члена арифметической прогрессии выглядит следующим образом:

aₙ = a₁ + (n — 1) · d,

где:

1. aₙ — n-й член прогрессии;
2. a₁ — первый член прогрессии;
3. d — разность прогрессии;
4. n — номер искомого члена.

Эта формула позволяет найти любой член прогрессии, если известны первый член, разность и номер члена.

Формулы арифметической прогрессии

Для работы с арифметической прогрессией используются следующие основные формулы.

1. Формула n-го члена

Чтобы найти n-й член арифметической прогрессии, используется формула:

aₙ = a₁ + (n — 1) · d

где:

1. aₙ — n-й член прогрессии;
2. a₁ — первый член прогрессии;
3. d — разность прогрессии;
4. n — номер искомого члена.

2. Сумма первых n членов

Сумма первых n членов арифметической прогрессии вычисляется по одной из двух формул:

Если известны первый и последний члены прогрессии:

Sₙ = (a₁ + aₙ) · n / 2

где:

1. Sₙ — сумма первых n членов;
2. a₁ — первый член;
3. aₙ — n-й член;
4. n — количество членов.

Если известны первый член и разность:

Sₙ = (2a₁ + (n — 1) · d) · n / 2

где:

1. d — разность прогрессии.

3. Разность арифметической прогрессии

Если известны первый и n-й члены прогрессии, разность d можно найти по формуле:

d = (aₙ — a₁) / (n — 1)

где:

1. aₙ — n-й член прогрессии;
2. a₁ — первый член;
3. n — номер n-го члена.

4. Среднее арифметическое

Любой член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних членов:

aₙ = (aₙ₋₁ + aₙ₊₁) / 2

где:

1. aₙ — текущий член;
2. аₙ₋₁ — предыдущий член;
3. aₙ₊₁ — следующий член.

Геометрическая прогрессия

📎 Геометрическая прогрессия — это числовая последовательность, в которой каждый следующий член получается из предыдущего умножением на одно и то же число. Это число называется знаменателем геометрической прогрессии и обозначается как q.

Формально:

bₙ₊₁ = bₙ · q

где:

1. bₙ — текущий член прогрессии;
2. bₙ₊₁ — следующий член прогрессии;
3. q — знаменатель прогрессии.

Пример: 2, 6, 18, 54, … (здесь q = 3).

Для нахождения n-го члена геометрической прогрессии используется формула:

bₙ = b₁ · qⁿ⁻¹

где:

1. bₙ — n-й член прогрессии;
2. b₁ — первый член прогрессии;
3. q — знаменатель прогрессии;
4. n — номер искомого члена.

Решение задач

Задача 1. Найдите 10-й член арифметической прогрессии, если a₁ = 3 и d = 4.

Решение:
Используем формулу n-го члена арифметической прогрессии:

aₙ = a₁ + (n — 1) · d

Подставляем известные значения:

a₁₀ = 3 + (10 — 1) · 4

а₁₀ = 3 + 9 · 4

a₁₀ = 3 + 36 = 39

Ответ: 39.

Задача 2. Найдите сумму первых 8 членов арифметической прогрессии, если a₁ = 5 и d = 2.

Решение:
Используем формулу суммы первых n членов:

Sₙ = (2a₁ + (n — 1) · d) · n / 2

Подставляем известные значения:

S₈ = (2 · 5 + (8 — 1) · 2) · 8 / 2

S₈ = (10 + 7 · 2) · 8 / 2

S₈ = (10 + 14) · 8 / 2

S₈ = 24 · 8 / 2 = 96

Ответ: 96.

Задача 3. В арифметической прогрессии a₃ = 7 и a₅ = 13. Найдите разность d и первый член a₁.

Решение:
Используем формулу n-го члена:

aₙ = a₁ + (n — 1) · d

Для a₃:

a₃ = a₁ + 2d = 7

Для a₅:

a₅ = a₁ + 4d = 13

Составляем систему уравнений:

a₁ + 2d = 7

a₁ + 4d = 13

Вычитаем первое уравнение из второго:

(a₁ + 4d) — (a₁ + 2d) = 13 — 7

2d = 6 ⇒ d = 3

Подставляем d = 3 в первое уравнение:

a₁ + 2 · 3 = 7

a₁ + 6 = 7 ⇒ a₁ = 1

Ответ: d = 3, a₁ = 1

---

Числовые последовательности, такие как арифметическая и геометрическая прогрессии, играют важную роль в математике и её приложениях. Мы рассмотрели определения, свойства, формулы и способы задания арифметической прогрессии, а также решили несколько задач. Эти знания помогут не только в учёбе, но и в реальной жизни, например, при расчётах в финансах, в физике или информатике.

Если возникают трудности с пониманием темы, воспользуйтесь материалами статьи или обратитесь за дополнительной помощью к репетиторам нашей онлайн-школы. Первый урок по форме ниже — бесплатный!