
Признаки равенства треугольников
В школьной программе геометрии признаки равенства треугольников начинают изучать в 7-м классе. Эти признаки являются одними из ключевых понятий, которые позволяют определить, равны ли два треугольника, не сравнивая все их элементы. Знание признаков равенства треугольников помогает решать задачи на доказательство и вычисление различных величин.
В этой статье мы подробно разберём три основных признака равенства треугольников, их доказательства, а также научимся применять их для решения задач.
Первый признак равенства треугольников
Формулировка: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство первого признака равенства треугольников:
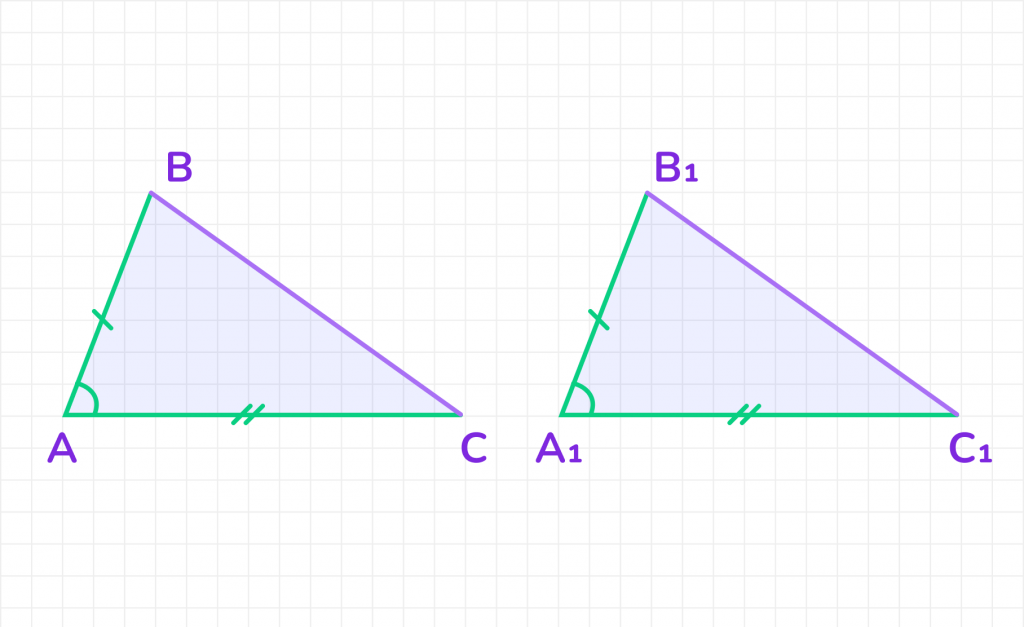
1. Рассмотрим два треугольника ABC и A₁B₁C₁, где:
- AB = A₁B₁ (равные стороны).
- AC = A₁C₁ (равные стороны).
- ∠BAC = ∠B₁A₁C₁ (равные углы).
2. Наложим ΔABC на ΔA₁B₁C₁ так, чтобы:
- Вершина A совпала с вершиной A₁.
- Сторона AB совпала со стороной A₁B₁.
- Сторона AC совпала со стороной A₁C₁.
3. Поскольку ∠BAC = ∠B₁A₁C₁, сторона BC совпадёт со стороной B₁C₁.
4. Таким образом, треугольники полностью совмещаются, что означает их равенство.
Второй признак равенства треугольников
Формулировка: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство второго признака равенства треугольников:
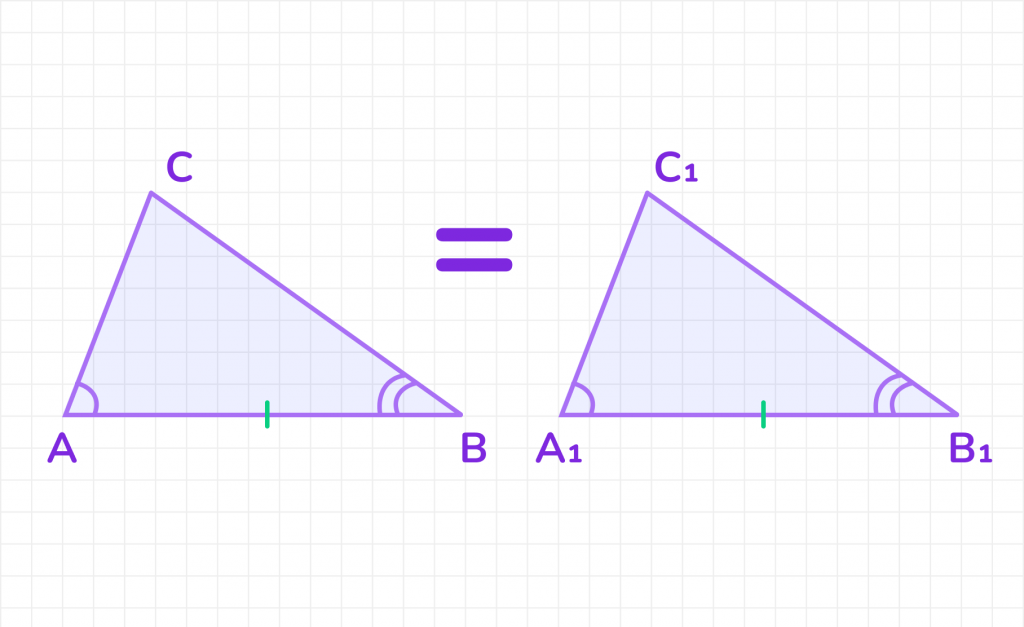
1. Рассмотрим два треугольника ABC и A1B1C1, где:
- AB = A₁B₁ (равные стороны).
- ∠CAB = ∠C₁A₁B₁ (равные углы).
- ∠ABC = ∠A₁B₁C₁ (равные углы).
2. Наложим треугольник ABC на треугольник A₁B₁C₁ так, чтобы:
- Вершина A совпала с вершиной A₁.
- Сторона AB совпала со стороной A₁B₁.
3. Поскольку ∠CAB = ∠C₁A₁B₁, сторона AC совпадёт со стороной A₁C₁.
4. Аналогично, поскольку ∠ABC = ∠A₁B₁C₁, сторона BC совпадёт со стороной B₁C₁.
5. Таким образом, треугольники полностью совмещаются, что означает их равенство.
Третий признак равенства треугольников
Формулировка: если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Доказательство третьего признака равенства треугольников:
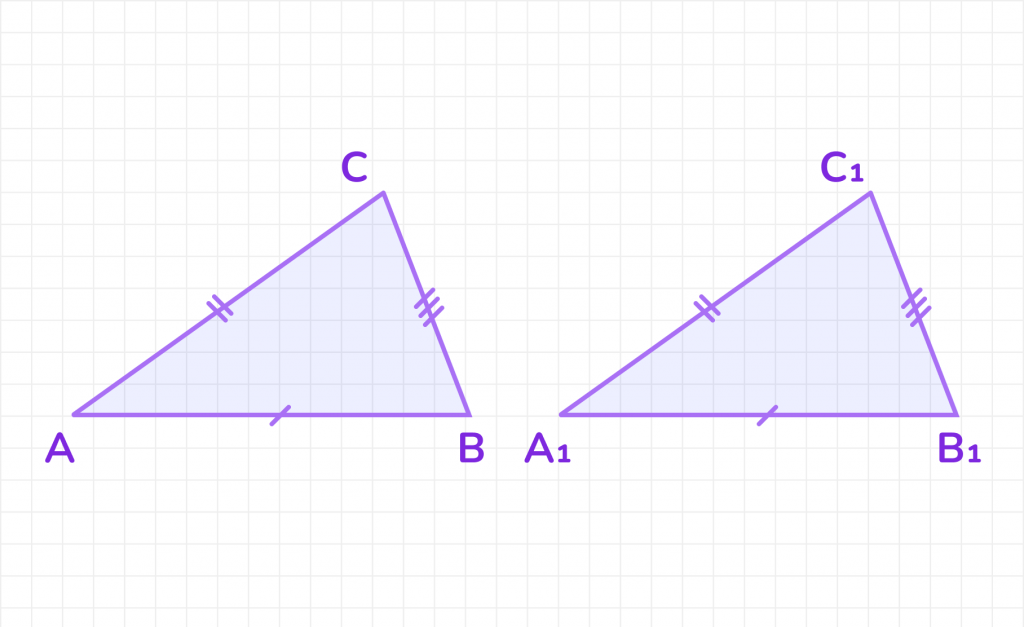
1. Рассмотрим два треугольника ABC и A₁B₁C₁, где:
- AB = A₁B₁.
- AC = A₁C₁.
- BC = B₁C₁.
2. Наложим ΔABC на ΔA₁B₁C₁ так, чтобы:
- Сторона AB совпала со стороной A₁B₁.
- Сторона AC совпала со стороной A₁C₁.
3. Поскольку BC = B₁C₁, точка C совпадёт с точкой C₁.
4. Таким образом, треугольники полностью совмещаются, что означает их равенство.
Решение задач на признаки равенства треугольников
Задача 1
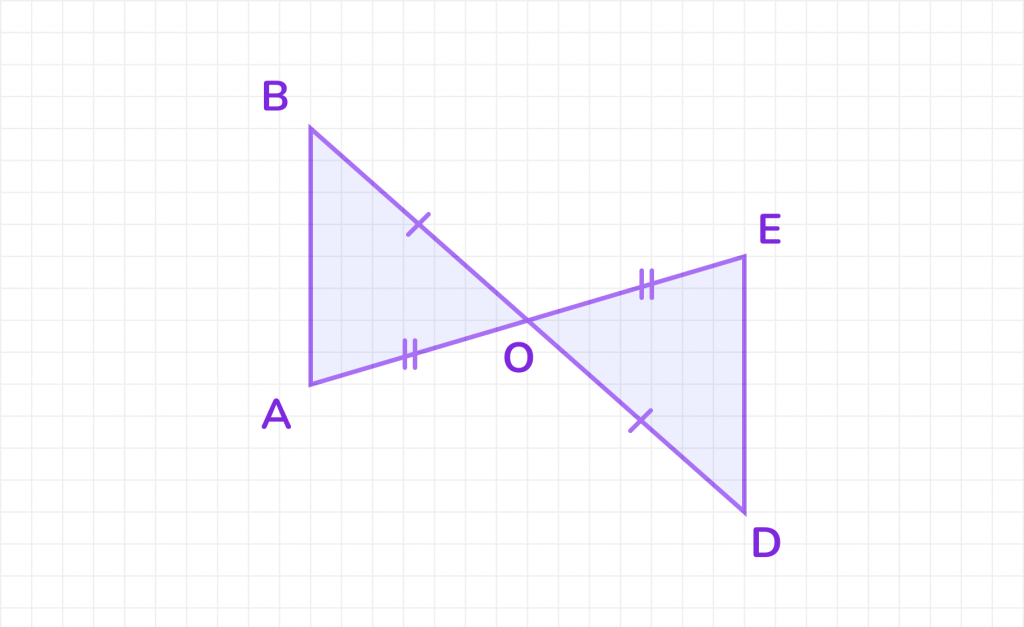
Доказать: ΔAOB = ΔDOE.
Доказательство:
- BO = OD и AO = OE (по условию).
- ∠BOA = ∠DOE, так как это вертикальные углы.
- ΔAOB = ΔDOE по двум сторонам и углу между ними (по первому признаку равенства треугольников).
Задача 2
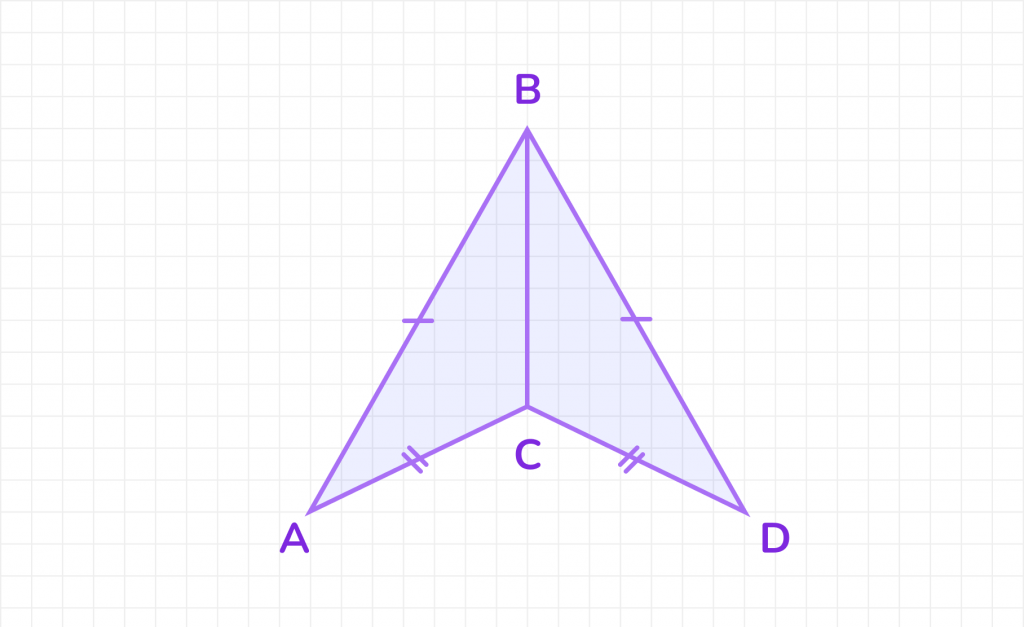
Доказать: ΔABC = ΔBCD.
Доказательство:
- BA = BD и AC = CD (по условию).
- BC – общая сторона.
- ΔABC = ΔBCD по трём сторонам (по третьему признаку равенства треугольников).
Задача 3
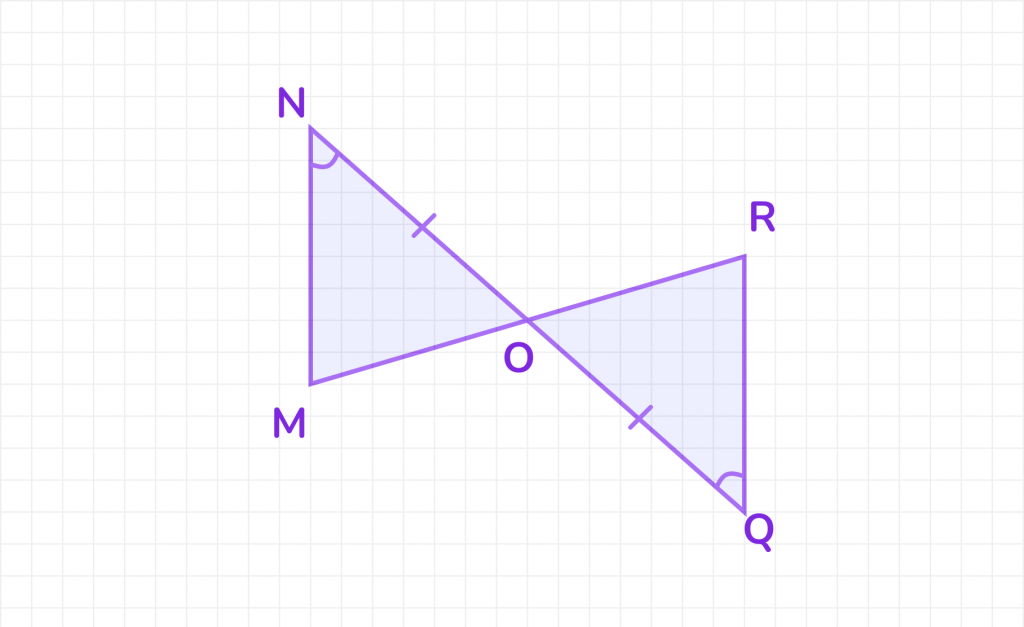
Доказать: ΔMON = ΔROQ.
Доказательство:
- NO = QO (по условию), ∠MNO = ∠RQO (по условию).
- ∠MON = ∠QOR, так как это вертикальные углы.
- ΔMON = ΔROQ по стороне и двум прилежащим к ней углам (по второму признаку равенства треугольников).

Признаки равенства треугольников — это важные инструменты в геометрии, которые позволяют быстро и точно определять равенство треугольников. В статье мы рассмотрели три основных признака, их доказательства и примеры использования. Эти знания помогут ученикам 7-го класса решать задачи на доказательство и вычисление, а также подготовиться к более сложным темам по геометрии.
Если ребёнок испытывает трудности в работе с признаками равенства треугольников, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия!
 60
60
 24
24
 10
10








Всё ясно и понятно
не могу понять,ну никак