
Как посчитать проценты от числа
Проценты — это важное понятие в математике, которое помогает нам выражать части целого в удобной форме. Школьники начинают знакомиться с ним в 5–6-х классах. В повседневной жизни мы часто сталкиваемся с процентами: от скидок в магазинах до расчётов налогов и процентов по кредитам. В этой статье мы разберёмся, как правильно находить проценты от числа, используя различные методы и примеры.
Основные понятия
Процент — это единица измерения, которая обозначает часть от ста. Проще говоря, процент — это одна сотая часть какого-то числа.
Процент — это 1/100 от числа. То есть, если у вас есть число, например, 200, и вы хотите найти 1% от этого числа, вам нужно разделить его на 100.
Если 1% от числа — это 1 сотая часть этого числа, то 10% — это 10 сотых, 25% — это 25 сотых и так далее.
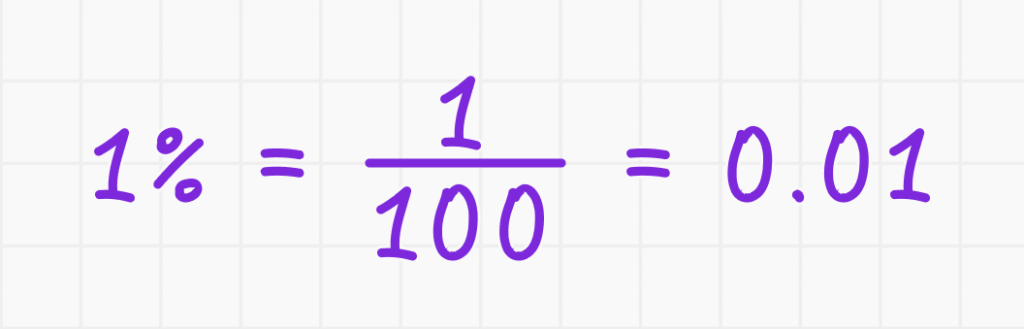
Чтобы перевести любой процент p в дробь, используйте формулу:
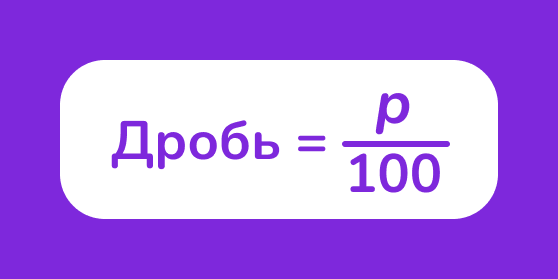
Затем упростите дробь, если это необходимо.
Процентное значение обозначает количество сотых частей числа. Поэтому, чтобы перевести процент в десятичную дробь, достаточно разделить процентное значение на 100. Это позволяет работать с процентами в более удобной форме, особенно когда нужно выполнять математические операции.
Чтобы перевести дробь в проценты, нужно выполнить несколько простых шагов. Процесс включает в себя преобразование дробного значения в десятичную дробь, а затем умножение на 100, чтобы получить процентное значение.
Шаги по переводу дробей в проценты
- Преобразуйте дробь в десятичную дробь. Для этого разделите числитель дроби на её знаменатель.
- Умножьте результат на 100. Это преобразует десятичную дробь в проценты.
- Добавьте знак процента (%). Это завершает процесс и показывает, что значение выражено в процентах.
Пример перевода дроби в проценты
Дробь 3/4 преобразуем в десятичную дробь:
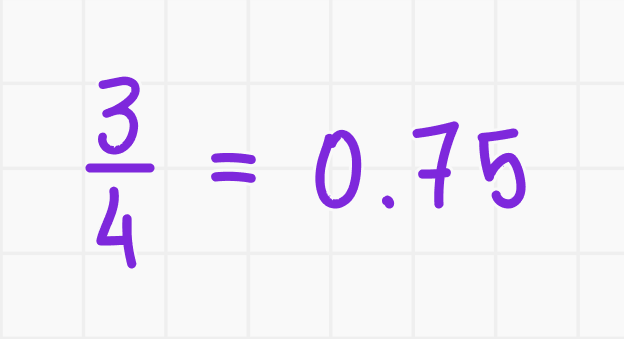
Умножаем на 100: 0,75 ∙ 100 = 75.
Ответ:
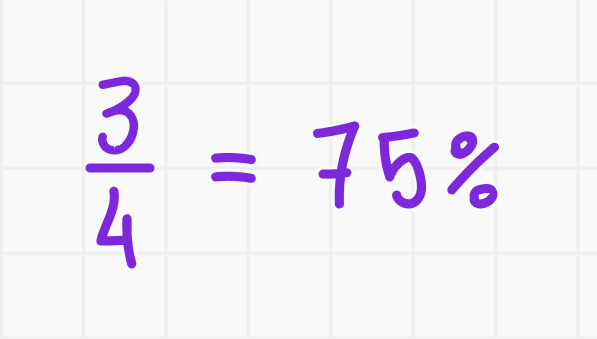
Правила нахождения процентов от числа
Чтобы найти процент от числа, следуйте этим шагам:
- Переведите процент в дробь: процент нужно преобразовать в дробь, деля его на 100. Например, 20% = 20/100 = 0,20.
- Умножьте на число: умножьте эту дробь на число, от которого нужно найти процент. Например, чтобы найти 20% от 50, умножьте 0,20 на 50.
Формула нахождения процентов от числа:

1. Нахождение одного процента от числа
Чтобы найти один процент от числа, используйте следующую формулу:

Например, чтобы найти 1% от 80, разделите 80 на 100: 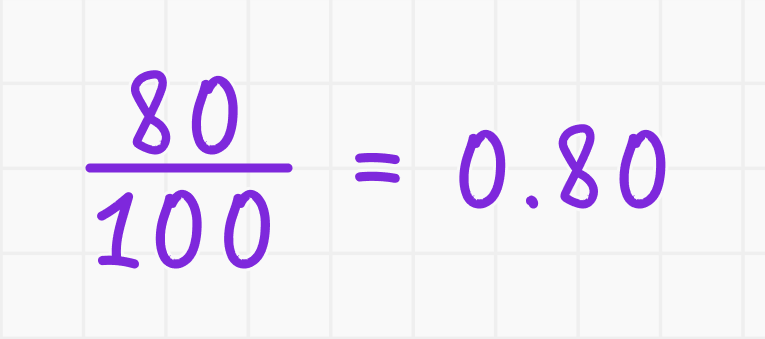
Таким образом, 1% от 80 равен 0,80.
2. Перевод процентов в десятичную дробь
Процент можно легко перевести в десятичную дробь, разделив его на 100.
Примеры:
1. 25% в виде десятичной дроби:
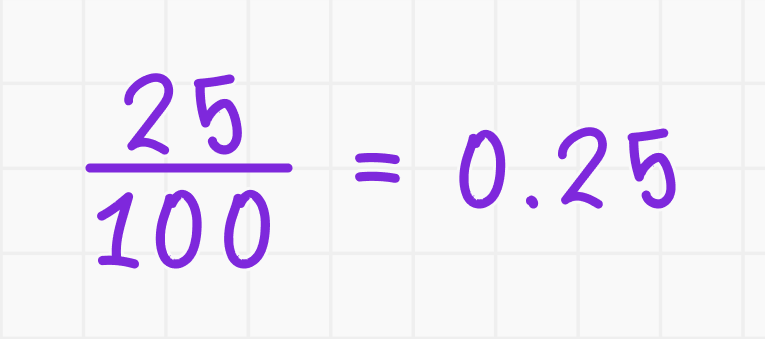
2. 75% в виде десятичной дроби:
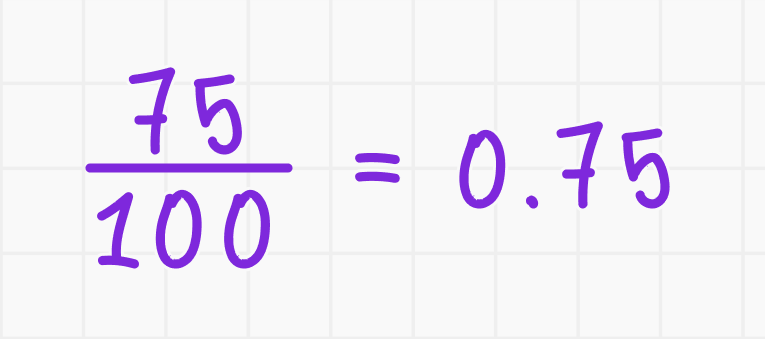
3. Составление пропорции
Пропорция — это уравнение, в котором два отношения равны. Она помогает решить задачи, связанные с процентами.
Пример:
Если 30% от числа x равно 60, найдите x.
1. Составьте пропорцию:
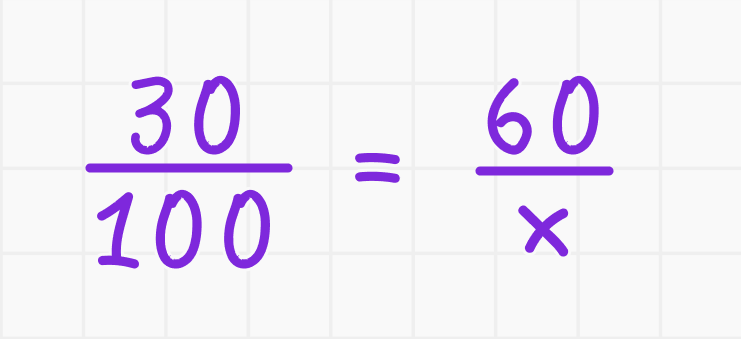
2. Перемножьте крест-накрест:
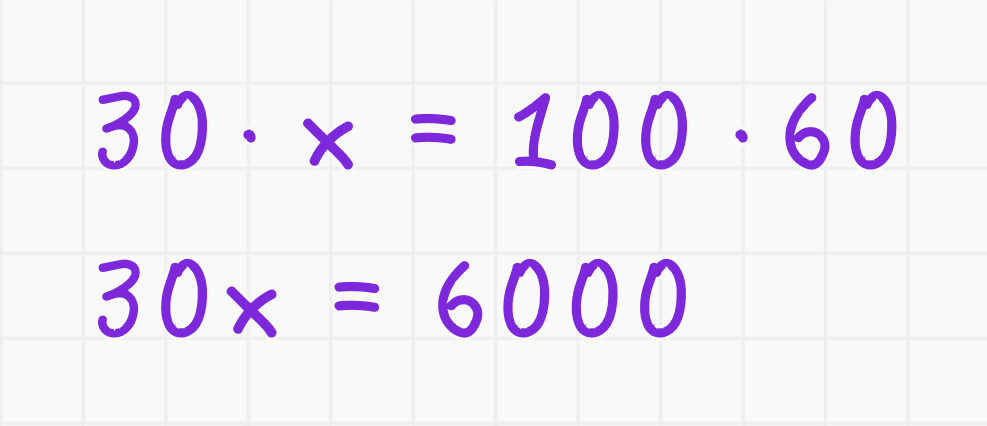
3. Разделите обе стороны на 30:
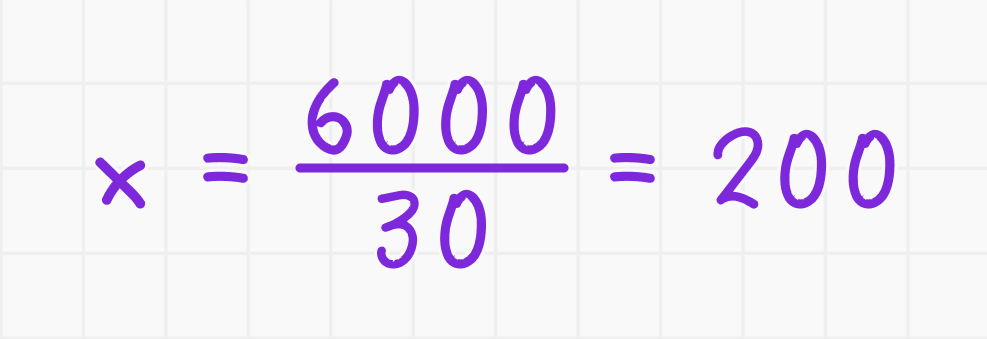
3. Соотношения чисел
Соотношение между числами можно выразить в процентах, если одно число является частью другого.
Пример:
Если в классе 30 учеников, из которых 12 — девочки, то какое процентное соотношение девочек в классе?
1. Используйте формулу:

2. Подставьте значения:
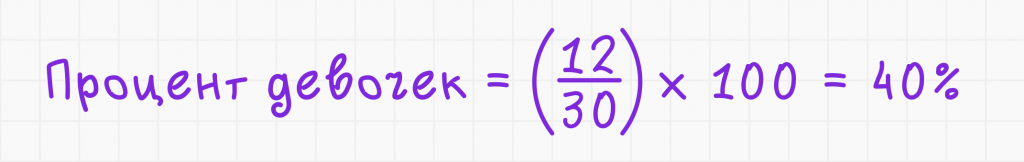
Решение задач на нахождение процентов от числа
Задача 1. Найдите 15% от 200.
- Переведите 15% в десятичную дробь: 15% = 0,15.
- Умножьте на 200: 0,15 ∙ 200 = 300.
- Ответ: 15% от 200 равно 30.
Задача 2. Если число увеличилось на 25% и стало 150, какое было первоначальное число?
- Пусть первоначальное число — x. После увеличения на 25% оно стало 150: x + 0,25x = 150.
- 1,25x = 150
- Разделите обе стороны на 1,25:
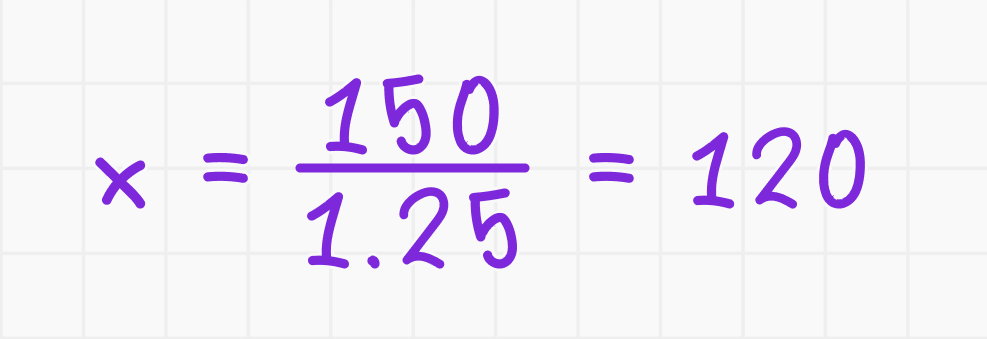
Ответ: первоначальное число было 120.
Задача 3. 60% от какого числа равно 90?
1. Составьте пропорцию:
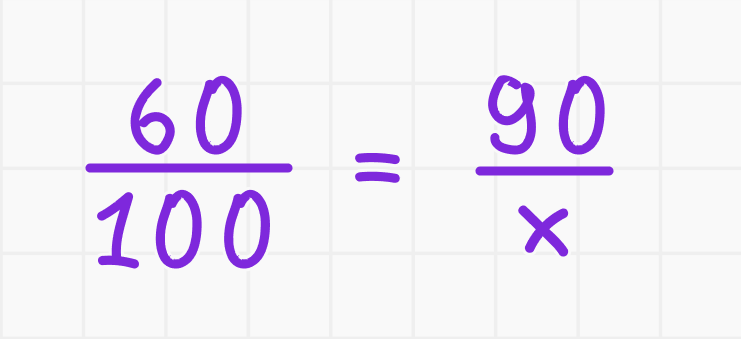
2. Перемножьте крест-накрест: 60x = 9000.
3. Разделите обе стороны на 60:
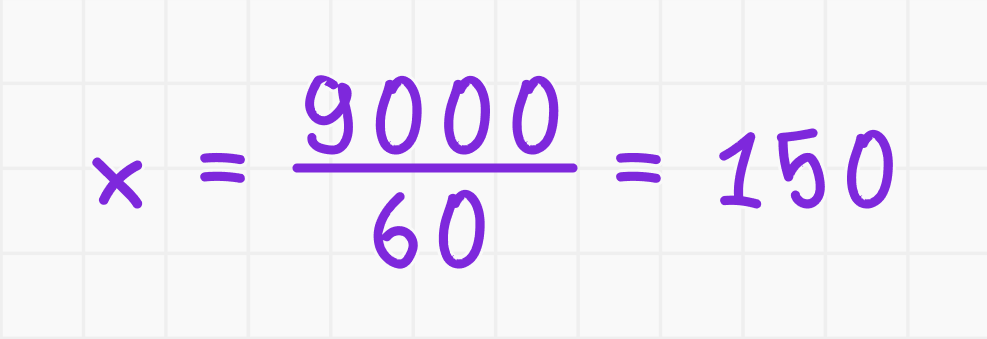
Ответ: искомое число равно 150.
Задача 4. Какой процент составляет число 45 от числа 360?
1. Используйте формулу:
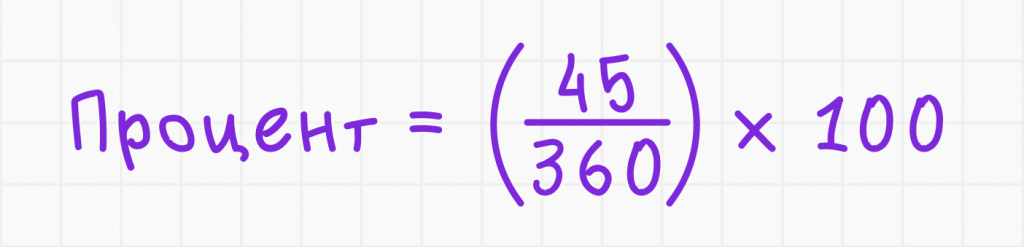
2. Выполните расчёт:
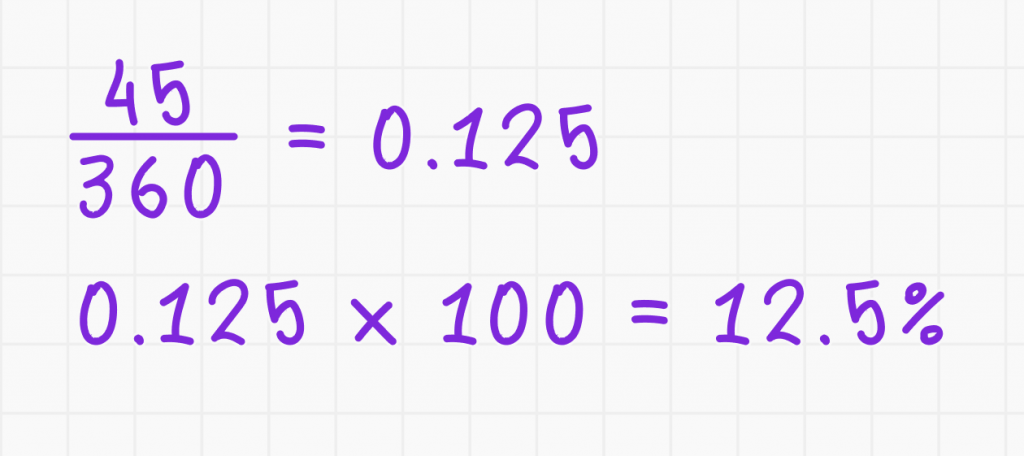
Ответ: 45 составляет 12,5% от 360.
Задача 5. После повышения на 40% цена товара стала 140 рублей. Какая была исходная цена?
1. Пусть исходная цена — x. После повышения на 40% она стала 140 рублей: x + 0,40 = 140;
1,40x = 140.
2. Разделите обе стороны на 1,40:

Ответ: исходная цена была 100 рублей.
Задача 6. На сколько процентов число 100 больше числа 80?
1. Найдите разницу между числами: 100 — 80 = 20.
2. Найдите процентное соотношение этой разницы к исходному числу:


3. Процентное увеличение = 0,25 — это 25%.
Ответ: число 100 больше числа 80 на 25%.
Знание того, как находить проценты от числа, полезно в различных ситуациях. Проценты позволяют сравнивать, анализировать и представлять данные в удобной форме. С помощью формул и методов, представленных в этой статье, можно легко решать задачи на нахождение процентов и применять их в повседневной жизни и учёбе.
Если ребёнок испытывает трудности в нахождении процентов от числа, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия 💜
 51
51
 17
17
 15
15








Я ничего не понял, а у меня завтра контроша 😢😢
Супер
Женя, добрый день! Первый урок с репетитором — бесплатный. Финальная стоимость занятий зависит от количества уроков в пакете, квалификации преподавателя, длительности занятия и направления подготовки.
Сколько стоит один час с репетитором?