Десятичные дроби: как решать

Десятичные дроби — важный раздел математики в 5–6-х классах. Знание об их свойствах и умение выполнять основные арифметические операции с ними помогает решать различные задачи и осуществлять повседневные расчёты. В этой статье мы подробно рассмотрим определение, свойства, запись, чтение, преобразования и действия с десятичными дробями.

Десятичные дроби: определение

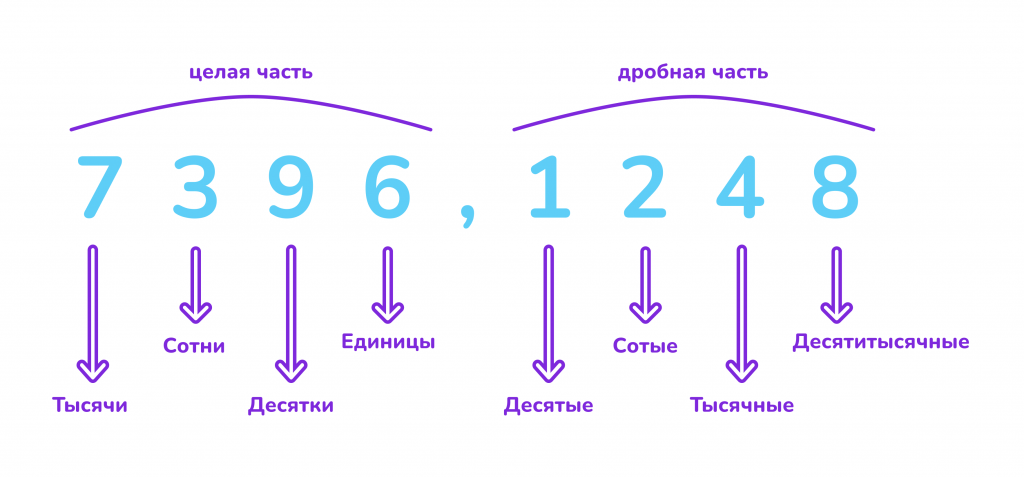
Десятичная дробь — это дробь, у которой знаменатель является степенью числа 10. Она записывается с помощью запятой, разделяющей целую часть и дробную часть.

В числе 3,75 целая часть — 3, а дробная часть — 75 сотых.

Десятичные дроби: свойства

1. Ограниченность: десятичные дроби могут быть конечными (например, 0.25) или бесконечными периодическими (например, 0.333…).
2. Сравнение: для сравнения десятичных дробей выравнивайте количество цифр после запятой и сравнивайте числа.
3. Прибавление и вычитание: операции сложения и вычитания выполняются, выравнивая запятые.
4. Умножение и деление: операции умножения и деления проводятся, как с обычными дробями, с учётом запятых.

Главное свойство десятичной дроби: если к десятичной дроби справа приписать один или несколько нулей, её величина не изменится.

1. 2,5 = 2,50.
2. 4,075 = 4,0750.

Запись десятичных дробей

Запись десятичных дробей требует правильного размещения запятой. Количество цифр после запятой определяет точность дроби.

1. 7,1 — семь целых и одна десятая.
2. 0,005 — пять тысячных.

Чтение десятичных дробей

Чтение десятичных дробей включает произнесение целой и дробной частей отдельно.

1. 4,62 читается как «четыре целых шестьдесят две сотых».
2. 0,075 читается как «ноль целых семьдесят пять тысячных».

Преобразования десятичных дробей

Преобразование между десятичными и обыкновенными дробями — важный навык.

1. Из десятичной в обыкновенную дробь

Запишите числитель как дробь от 1 и укажите степень десяти. Примеры:

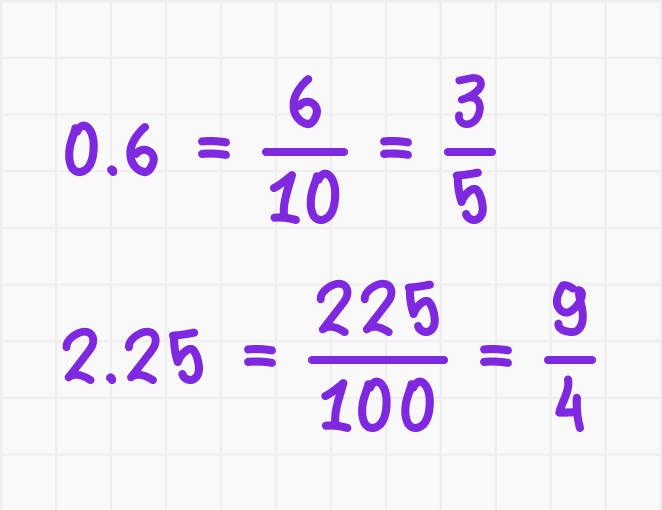
2. Из обыкновенной дроби в десятичную

Разделите числитель на знаменатель. Примеры:

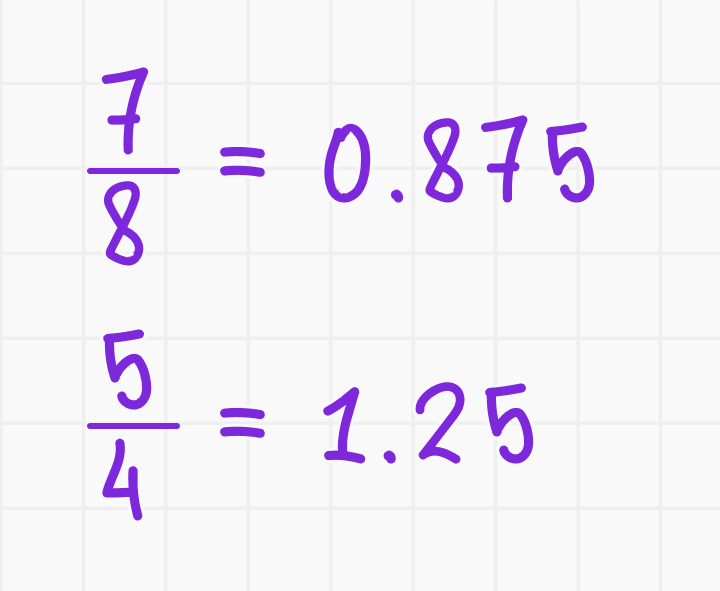
Действия с десятичными дробями

1. Десятичные дроби: сложение и вычитание

1. Выравнивание запятых: убедитесь, что все дроби имеют одинаковое количество знаков после запятой.
2. Сложение и вычитание: выполняйте операции как с целыми числами.

Примеры:

1. 3,4 + 2,15 = 5,55.
2. 7,8 — 1,35 = 6,45.

2. Десятичные дроби: умножение

1. Игнорирование запятых: умножайте как обычные числа.
2. Подсчёт знаков после запятой: сложите количество знаков после запятой в обоих множителях.
3. Размещение запятой: в результате умножения разместите запятую с учётом общего числа знаков после запятой.

Примеры:

1. 0,4 ∙ 0,5 = 0,20 = 0,2.
2. 2,5 ∙ 3,6 = 9,00 = 9

3. Десятичные дроби: деление

1. Преобразование делителя: перенесите запятую в делителе вправо, чтобы он стал натуральным числом. Сделайте то же самое с делимым.
2. Деление: выполните деление как с целыми числами.
3. Постановка запятой: расположите запятую в ответе, учитывая количество знаков после запятой в делимом.

Примеры:

1. 4,8 : 0,6 = 8,0 = 8.
2. 7,2 : 0,4 = 18,0 = 18.

4. Десятичные дроби: сравнение

1. Выравнивание знаков после запятой: добавьте нули по необходимости, чтобы дроби имели одинаковое количество знаков после запятой.
2. Сравнение чисел: сравните числа, учитывая знаки после запятой.

Примеры:

1. 3,25 и 3,250 равны.
2. 4,01 больше, чем 4,001.

Десятичные дроби: практика решения задач

1. Найдите сумму 2,45 и 3,75.
2. Вычислите разность 6,8 и 2,55.
3. Умножьте 0,4 на 5,6.
4. Разделите 9,6 на 1,2.

Решение:

1. 2,45 + 3,75 = 6,20 = 6,2.
2. 6,8 — 2,55 = 4,25.
3. 0,4 ∙ 5,6 = 2,24.
4. 9,6 : 1,2 = 8,0 = 8.

Десятичные дроби являются важным инструментом в математике и повседневной жизни. Знание их свойств, умение выполнять арифметические операции и правильно преобразовывать дроби помогают эффективно решать задачи и осуществлять расчёты. 

Если ребёнок испытывает трудности в работе с десятичными дробями, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия 💜