
Какие числа называются целыми
В 6-м классе школьной программы учащиеся начинают более подробно изучать различные виды чисел, включая целые числа. Понимание целых чисел и их свойств является основой для дальнейшего изучения алгебры и других разделов математики. В этой статье мы рассмотрим определение целых чисел, их свойства, виды, применение и решение задач с их использованием.
Определение целого числа
Целые числа включают все натуральные числа, их отрицательные значения и ноль. Множество целых чисел обычно обозначается буквой Z и выглядит следующим образом:
Z = { …, -3, -2, -1, 0, 1, 2, 3, … }.
Примеры целых чисел: -5, 0, -7, 1 000, 56.
Целые числа могут быть изображены на числовой прямой. Числовая прямая — это графическое представление чисел, где каждая точка соответствует определённому числу. На этой прямой ноль занимает центральное положение, положительные числа находятся справа от нуля, а отрицательные — слева.

Свойства целых чисел
1. Замкнутость: целые чиcла замкнуты относительно операций сложения, вычитания и умножения. Это означает, что сумма, разность и произведение любых двух целых чисел также являются целыми числами.
2. Ассоциативность:
— (a + b) + c = a + (b + c);
— (a · b) · c = a · (b · c).
3. Коммутативность:
— a + b = b + a;
— a · b = b · a.
4. Существование нуля и единицы:
— a + 0 = a;
— a · 1 = a.
5. Дистрибутивность умножения относительно сложения:
— a · (b + c) = (a · b) + (a · c).
Положительные и отрицательные целые числа
Целые чиcла делятся на положительные, отрицательные и ноль.
Положительные целые чиcла: это числа больше нуля (1, 2, 3, …).
Отрицательные целые чиcла: это чиcла меньше нуля (-1, -2, -3, …).
Ноль: не является ни положительным, ни отрицательным числом, но включается в множество целых чисел.
Примеры:
- Положительные: 3, 15, 100.
- Отрицательные: -4, -20, -100.
- Ноль: 0.
Неположительные и неотрицательные целые числа
Неположительные целые числа: включают все отрицательные целые числа и ноль (≤ 0).
Неотрицательные целые числа: включают все положительные целые числа и ноль (≥ 0).
Примеры:
- Неположительные: 0, -1, -2, -3.
- Неотрицательные: 0, 1, 2, 3.
Множества и подмножества целых чисел
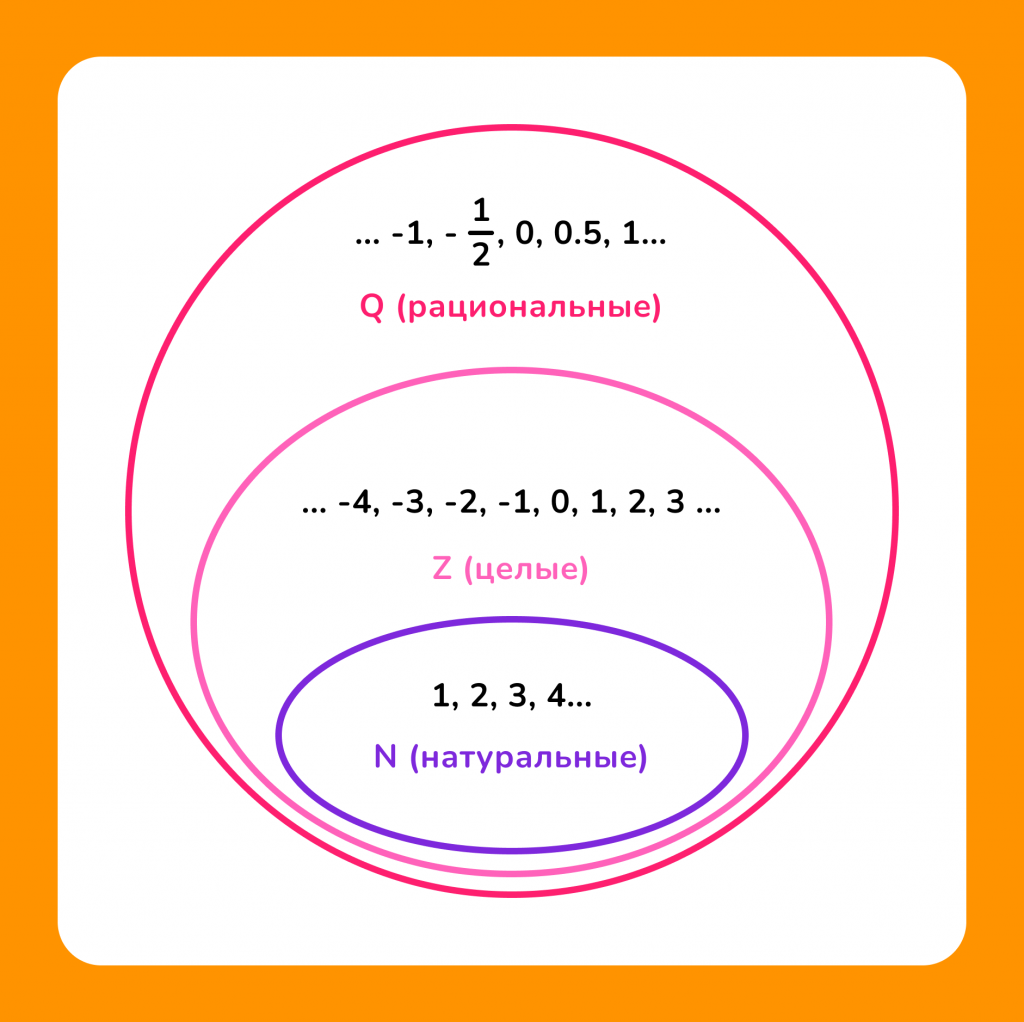
Целые числа являются частью более широкого множества чисел. Рассмотрим основные множества чисел и их подмножества:
1. Натуральные чиcла (N): это положительные целые числа, начиная с 1 (1, 2, 3, …).
2. Целые чиcла (Z): включают натуральные числа, их отрицательные значения и ноль.
3. Рациональные чиcла (Q): это числа, которые могут быть представлены в виде дроби a/b, где a и b — целые чиcла, и b ≠ 0.
Применение целых чисел
Целые чиcла широко используются в различных областях математики и реальной жизни:
- Финансы: представление прибылей и убытков.
- Температурные шкалы: измерение температур выше и ниже нуля.
- Координатные системы: представление точек на координатных осях.
- Ежедневные ситуации: подсчёт предметов, расчёт изменений в количестве чего-либо.
Решение задач с целыми числами
Пример 1. Сложение целых чисел.
Найдите сумму чисел 7 и -5.
Решение: 7 + (-5) = 2.
Пример 2. Вычитание целых чисел.
Найдите разность чисел -3 и 4.
Решение: -3 — 4 = -7.
Пример 3. Умножение целых чисел.
Найдите произведение чисел -6 и 3.
Решение: -6 ∙ 3 = -18.
Пример 4. Деление целых чисел.
Найдите частное чисел -20 и 5.
Решение: -20 ÷ 5 = -4.
Пример 5. Целые чиcла на числовой прямой.
Найдите целые чиcла между -3 и 2 на числовой прямой.
Решение. Целые чиcла в этом промежутке -2, -1, 0, 1.
Пример 6. Количество целых чисел между числами.
Сколько целых чисел находится между -10 и 5?
Решение. Целые чиcла в этом промежутке: -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4.
Количество целых чисел: 14.
Пример 7. Количество целых чисел между числами.
Сколько целых чисел находится между 3 и 12?
Решение. Целые чиcла в этом промежутке: 4, 5, 6, 7, 8, 9, 10, 11.
Количество целых чисел: 8.
Целые чиcла являются основой для более сложных математических действий. Они включают положительные и отрицательные чиcла, а также ноль, и обладают рядом важных свойств, таких как замкнутость, ассоциативность и коммутативность. Понимание и умение работать с целыми числами является важным шагом в развитии математической грамотности учащихся и их способности решать разнообразные математические задачи.
Если ребёнок испытывает трудности в работе с целыми числами, воспользуйтесь материалами статьи для тренировки или приходите к нам на занятия 💜
 7
7
 8
8
 5
5








Доходчиво и понятно. Спасибо большое!
Очень помогли