Параллелепипед и его виды

В 4–5 классах школьной программы учащиеся начинают изучать параллелепипед. Это одна из важных геометрических фигур в математике. Параллелепипеды можно найти и в повседневной жизни. Это могут быть, например, коробки, книги, здания и т. д. Понимание свойств и видов параллелепипедов помогает ученикам, прежде всего, развивать пространственное мышление и решать практические задачи.

В этой статье мы рассмотрим, что такое параллелепипед, его элементы и виды. А также научимся решать задачи, связанные с ним.

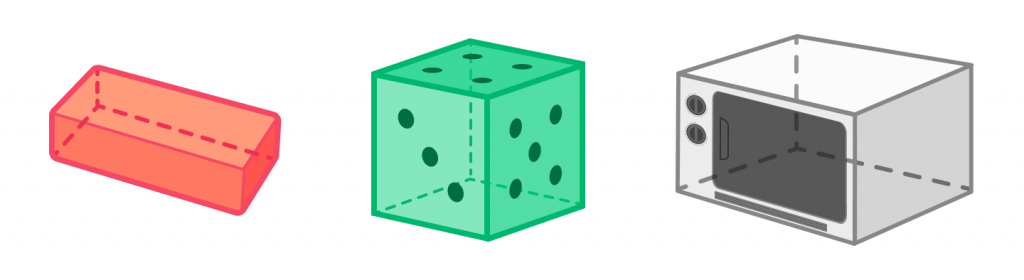
Что такое параллелепипед

Параллелепипед — это трёхмерная геометрическая фигура, у которой все грани представляют собой параллелограммы. Параллелепипед можно представить как шестигранник, у которого противоположные грани параллельны и равны между собой. Прежде всего он состоит из двух параллельных оснований и боковых граней, которые соединяют эти основания. Важно отметить, что все грани параллелепипеда являются плоскими фигурами. А его объём определяется как пространство, занимаемое внутри этой фигуры.

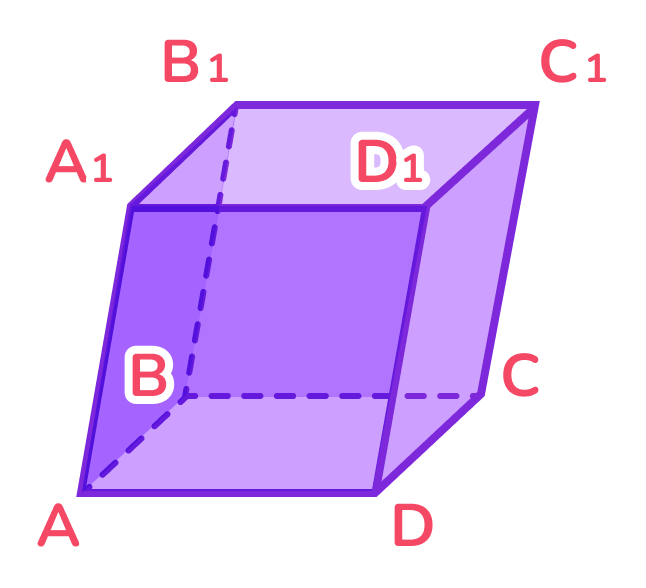
Параллелепипед и элементы

Параллелепипед состоит из нескольких ключевых элементов, а именно: граней, вершин и рёбер.

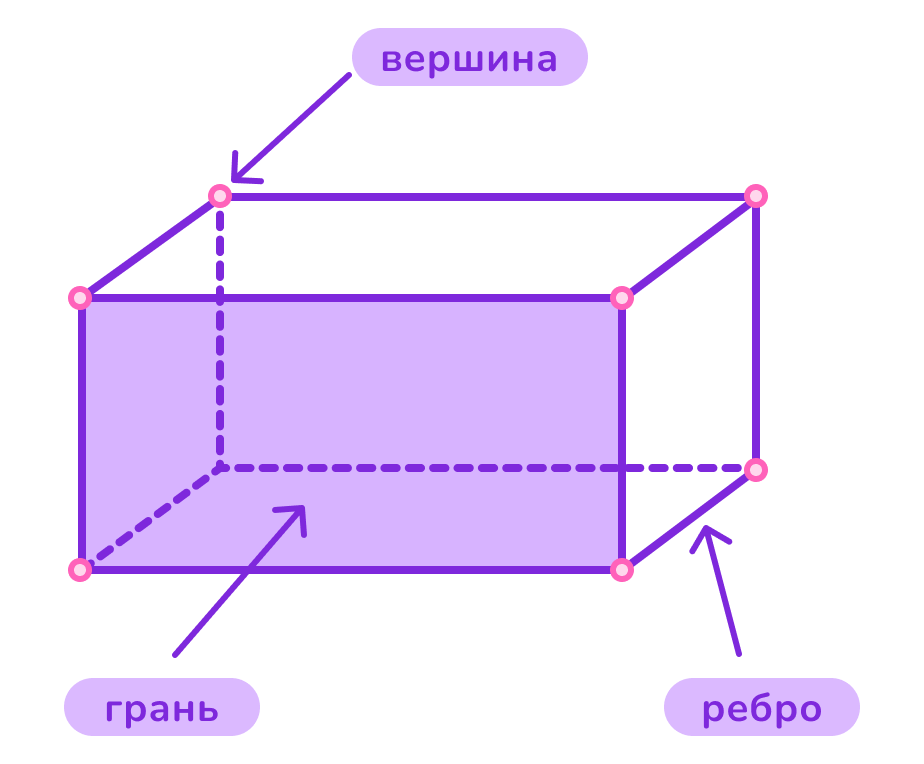
➜ Грань — это плоская поверхность, которая ограничивает параллелепипед. Всего у параллелепипеда шесть граней. Каждая грань является параллелограммом.

➜ Вершина — это точка, где сходятся три ребра. Всего у параллелепипеда восемь вершин. Эти вершины являются углами, которые образуются при пересечении трёх граней.

➜ Ребро — это линия, где сходятся две грани. Всего у параллелепипеда двенадцать рёбер. Рёбра параллелепипеда можно рассматривать как стороны параллелограммов, образующих грани параллелепипеда.

Обозначение параллелепипеда

Параллелепипеды обозначаются буквами, которые представляют его вершины. Например, параллелепипед ABCDEFGH имеет восемь вершин, соединённых рёбрами. Грани обозначаются парами вершин, например, ABCD, EFGH и так далее. Также можно использовать три буквы для обозначения вершины и её двух соседних вершин. Для того, чтобы было ясно, какие грани и рёбра связаны между собой (ABC, EFG).

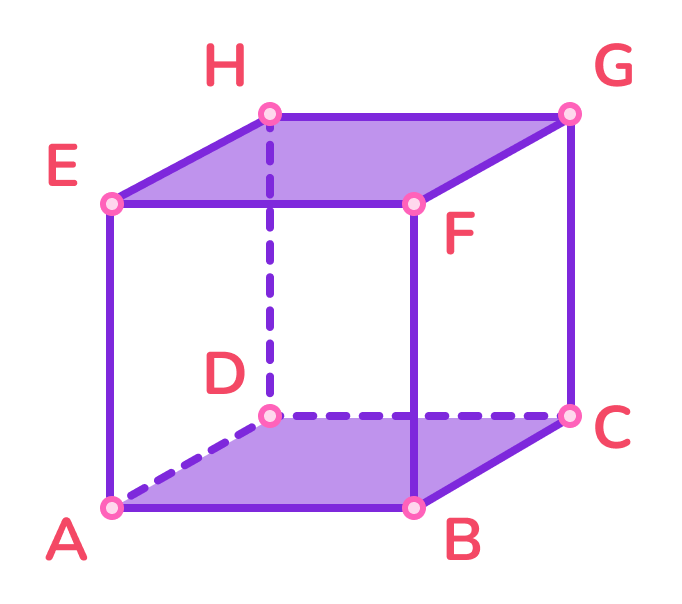
Виды параллелепипедов

Параллелепипеды могут быть разными в зависимости от формы и углов между гранями. Например, их основные виды.

➜ Прямой пaраллелепипед — это параллелепипед, у которого все углы между гранями прямые. То есть равны 90 градусам. Прямой параллeлепипед имеет все грани в виде прямоугольников или квадратов.

➜ Прямоугольный параллелепипед — это частный случай прямого параллелепипеда, у которого все грани являются прямоугольниками. Прямоугольный параллелепипед имеет три пары противоположных и равных по размеру граней.

➜ Куб — это частный случай прямоугольного параллелепипеда, у которого все грани равны и являются квадратами. В кубе все рёбра равны между собой. Куб является самым симметричным видом параллелепипеда.

Диагональ параллелепипеда

Диагональ параллелепипеда — это отрезок, соединяющий две противоположные вершины, которые не лежат на одной грани. В параллелепипеде четыре диагонали.

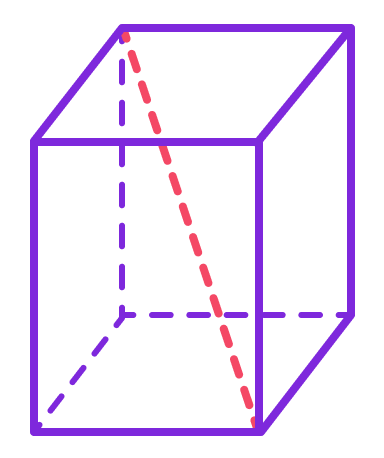
Параллелепипед: решение задач

Рассмотрим несколько задач для лучшего понимания параллелепипедов. Например:

➤ Задача 1. Найдите объём прямоугольного параллелепипеда.

Чтобы найти объём прямоугольного параллелепипеда, нужно перемножить длину, ширину и высоту. Формула выглядит так: V = a ∙ b ∙ c, где a, b и c — длины рёбер параллелепипеда.

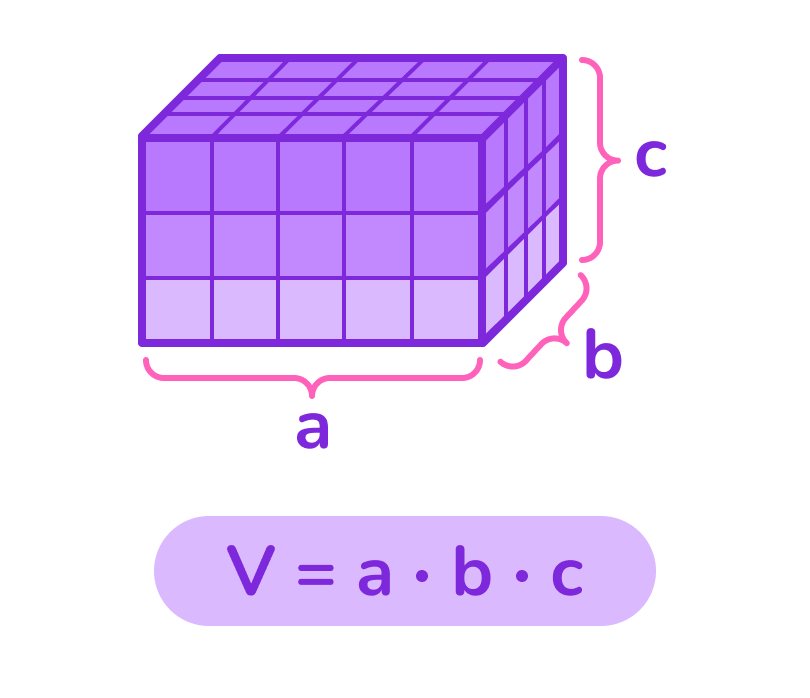
Пример решения:

Пусть a = 5 см, b = 3 см и c = 4 см. Тогда объём будет равен: V = 5 ∙ 3 ∙ 4 = 60 см³.

➤ Задача 2. Найдите площадь поверхности прямоугольного параллелепипеда.

Площадь поверхности прямоугольного параллелепипеда можно найти, сложив площади всех шести граней. Формула выглядит так: S = 2 ∙ (ab + bc + ac), где a, b и c — длины рёбер параллелепипеда.

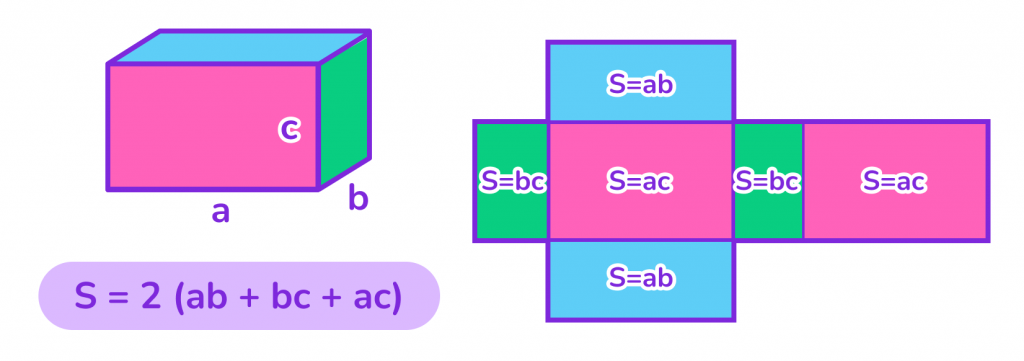
Пример решения:

Пусть a = 5 см, b = 3 см и c = 4 см. Тогда площадь поверхности будет: S = 2 ∙ (5 ∙ 3 + 3 ∙ 4 + 5 ∙ 4) = 2 ∙ (15 + 12 + 20) = 2 ∙ 47 = 94 см².

Итак, нам удалось узнать:

1. Параллелепипед — это трёхмерная фигура, состоящая из шести граней, восьми вершин и двенадцати рёбер.
2. Прямой параллелепипед имеет прямые углы между гранями.
3. Прямоугольный параллелепипед — это прямой параллелепипед, у которого все грани прямоугольные.
4. Куб — это частный случай прямоугольного параллелепипеда, где все грани квадратные и все рёбра равны.
5. Объём прямоугольного параллелепипеда равен произведению всех его измерений.
6. Площадь поверхности прямоугольного параллелепипеда равна сумме площадей всех его граней.

Если ребёнок испытывает трудности в работе с параллелепипедами, воспользуйтесь материалами статьи для тренировки. Или приходите на занятия к нашим репетиторам 💜